Long Questions: Algebra | Elementary Mathematics for PAT PDF Download

Q1: Determine two numbers so that one is greater by 21 than another and sum of them is 91.
Ans: Let x be one number.
Then, another number is x + 21.
By the given conditions,
x + (x + 21) = 91
⇒ 2x + 21 = 91
Add −21 on both sides of the equation.
2x + 21 + (−21) = 91 + (−21)
⇒ 2x + 21 − 21 = 91 − 21
⇒ 2x = 70
Divide 2 on both sides of the equation.
2x/2 = 702
⇒ x = 35
Hence, the required numbers are 35 and 35 + 21, that is 35, 56.

Q2: 5. Solve the following equation and justify the result.
3(a + 3) + 3(a − 1) = 5(a + 5).
Ans: The given equation is
3(a + 3) + 3(a - 1) = 5(a + 5)
⇒ 3a + 9 + 3a − 3 = 5a + 25, multiplying the terms.
⇒ 6a + 6 = 5a + 25, adding the like terms.
⇒ 6a − 5a = 25 − 6, by the method of transposition.
⇒ a = 19.
Justification: 
LHS = 3(a + 3) + 3(a − 1)
= 3(19 + 3) + 3(19 − 1)
= 3 × 22 + 3 × 18 = 66 + 54
= 120
Also, RHS = 5(a + 5)
= 5(19 + 5)
= 5 × 24
= 120
Thus, Left-hand-side = Right-hand-side. Hence, the required solution of the given equation is a = 19.

Q3: Solve the following equation and evaluate x by using the method of isolation.

Ans: The given equation is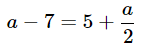

Add 7 on both sides of the equation.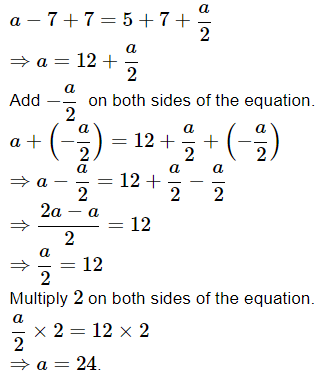

Hence, the required solution is a = 24.

Q4: Determine the solution of 3x = 12, by using the method of trial and errors.
Ans: The given equation is 3x = 12.
First substitute x = 1 into the given equation.
3x = 3 × 1 = 3 ≠ 12.
So, x ≠ 1.
Then, substitute x = 2 into the equation.
3x = 3 × 2 = 6 ≠ 12.
So, x ≠ 2.
Again, substitute x = 3 into the given equation.
3x = 3 × 3 = 9 ≠ 12.
Therefore, x ≠ 3.
Now, substitute x = 4 into the given equation.
Then 3x = 3 × 4 = 12.
Thus, x = 4 is the solution of the given equation.

Q5: Classify monomials, binomials, and trinomials from the following algebraic expressions.
y + 5, 6x³y, −8, −3pqr, a² + b² + z²
Ans: Recall that, sum of two terms is called binomials, sum of three terms is called trinomials and single algebraic term is called monomials.
The following table shows the required classifications.

Q6: Find the algebraic expression of the statements given below.
(a) 6 less than the quotient of x and y.
(b) The sum of the quotient of p, q and the product of p, q.
(c) One fourth of the sum of x and y.
(d) 8 removed from twice the term x.
Ans: (a) The required algebraic expression is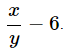

(b) The quotient of p, q is p/q.
The product of p, q is pq.
Therefore, the required algebraic expression is given by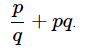

(c) The sum of x and y is x + y.
Therefore, the required algebraic expression is given by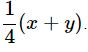

(d) Twice the term x is 2x.
Therefore, the required algebraic expression is 2x − 8.