Some Applications of Trigonometry Class 10 Notes Maths Chapter 9
Terminologies related to Heights and Distances
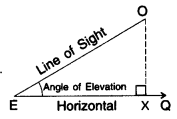
1. Line of Sight
When an observer looks from a point E (eye) at object O then the straight line EO between eye E and object O is called the line of sight.
2. Horizontal Line
When an observer looks from a point E (eye) to another point Q which is horizontal to E, then the straight line, EQ between E and Q is called the horizontal line.
3. Angle of Elevation
When the eye is below the object, then the observer has to look up from point E to object O. The measure of this rotation (angle θ) from the horizontal line is called the angle of elevation.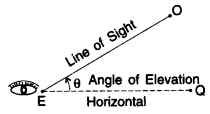
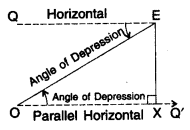
4. Angle of Depression
When the eye is above the object, then the observer has to look down from point E to the object. The horizontal line is now parallel to the ground. The measure of this rotation (angle θ) from the horizontal line is called the angle of depression.

How to convert the above figure into the right triangle.
Case I: Angle of Elevation is known
Draw OX perpendicular to EQ.
Now ∠OXE = 90°
ΔOXE is a rt. Δ, where
OE = hypotenuse
OX = opposite side (Perpendicular)
EX = adjacent side (Base)
Case II: Angle of Depression is known
(i) Draw OQ’parallel to EQ
(ii) Draw perpendicular EX on OQ’.
(iii) Now ∠QEO = ∠EOX = Interior alternate angles
ΔEXO is an rt. Δ. where
EO = hypotenuse
OX = adjacent side (base)
EX = opposite side (Perpendicular)
- Choose a trigonometric ratio in such a way that it considers the known side and the side that you wish to calculate.
- The eye is always considered at ground level unless the problem specifically gives the height of the observer.
- The object is always considered a point.
Example: The angle of elevation of a cloud from a point 60 m above a lake is
30 degrees and the angle of depression of the reflection of cloud in the lake is
60 degrees. Find the height of the cloud.
Sol:
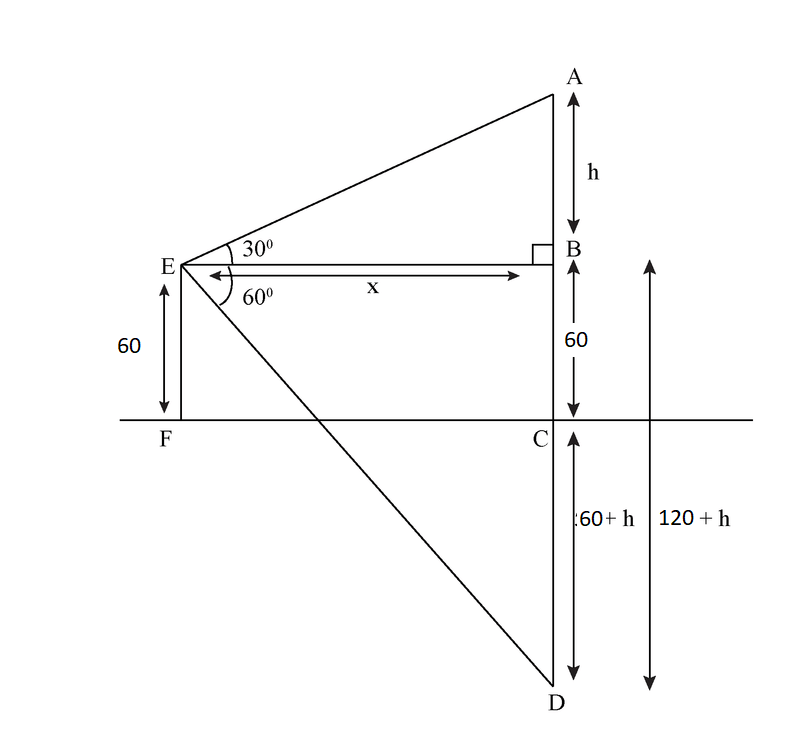
In ΔABE, we have
tan30 = h/x
1/√3 = h/x
⇒x=h√3
In ΔBDE, we have
tan60 = (120+h)/h√3
⇒√3 = (120 + h)/h√3
⇒3h = 120 + h
⇒2h=120
⇒h=60 m
Hence, height of cloud above the lake = 60+h=60+60=120m
Trick to remember Trigonometric Ratios
Some People Have
Curly Black Hair
Turning Permanent Black.
|
127 videos|680 docs|84 tests
|
FAQs on Some Applications of Trigonometry Class 10 Notes Maths Chapter 9
| 1. What is the angle of elevation in trigonometry? |  |
| 2. How is the angle of depression defined? |  |
| 3. What trigonometric ratios are commonly used in height and distance problems? |  |
| 4. Can you explain a real-life application of the angle of elevation? |  |
| 5. How do you solve problems involving angles of elevation and depression? |  |