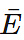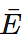Probability Class 10 Notes Maths Chapter 14
| Table of contents |

|
| What is Probability? |

|
| Sample Space |

|
| Sample Space- Examples |

|
| Some Solved Examples |

|
What is Probability?
- It is the numerical measurement of the degree of certainty.
- The theoretical probability associated with an event E is defined as “If there are ‘n’ elementary events associated with a random experiment and m of these are favourable to the event E then the probability of occurrence of an event is defined by P(E) as the ratio m/n.

- If P(E) = 1, then it is called a ‘Certain Event’.
- If P(E) = 0, then it is called an ‘Impossible Event’.
- The probability of an event E is a number P(E) such that: 0 ≤ P(E) ≤ 1
- An event having only one outcome is called an elementary event. The sum of the probabilities of all the elementary events of an experiment is 1.
- For any event E, P(E) + P (
 ) = 1, where
) = 1, where  stands for ‘not E’. E and
stands for ‘not E’. E and  is called complementary events.
is called complementary events. - Favourable outcomes are those outcomes in the sample space that are favourable to the occurrence of an event.
Sample Space
A collection of all possible outcomes of an experiment is known as sample space. It is denoted by ‘S’ and represented in curly brackets.
Sample Space- Examples
1. Tossing a coin

When we toss a coin, there can be only two outcomes i.e., either head or tail. So, the sample space will be, S = {H, T} where H is the head and T is the tail.
2. Tossing two coins together
When we flip two coins together, we have a total of 4 outcomes. H1 and T1 can be represented as heads and tails of the first coin. H2 and T2 can be represented as heads and tails of the second coin. So, the sample space will be,
S = {(H1, H2), (H1, T2), (T1, H2), (T1, T2)}
With this, we know that if we have ‘n’ coins, the possible number of outcomes will be 2n.
3. Rolling a dice
On rolling a die, we can have 6 outcomes. So the sample space will be, S = {1, 2, 3, 4, 5, 6}.
4. Rolling Two Dice Together
When we roll two dice together, we get double the outcomes than when we roll a single outcome. When we roll 2 dice together we get 36 outcomes (6 x 6 = 36).
Note:
- In probability the order in which events occur is important E1 & E3 are treated as different outcomes.
- A pack of playing cards consists of four suits called Hearts, Spades, Diamonds, and Clubs. Each suite consists of 13 cards.
Some Solved Examples
Example 1: A game of chance consists of spinning an arrow that comes to rest, pointing at any one of the numbers such as 1, 2, 3, 4, 5, 6, 7, or 8, and these are equally likely outcomes. What is the probability that it will point at? (i)8 (ii) Number greater than 2 (iii) Odd numbers
Sol:
Sample Space = {1, 2, 3, 4, 5, 6, 7, 8}
Total Numbers = 8
(i) Probability that the arrow will point at 8:
Number of times we can get 8 = 1
P (Getting 8) = 1/8.
(ii) Probability that the arrow will point at a number greater than 2:
Number greater than 2 = 3, 4, 5, 6, 7, 8.
No. of numbers greater than 2 = 6
P (Getting numbers greater than 2) = 6/8 = 3/4.
(iii) Probability that the arrow will point at the odd numbers:
Odd number of outcomes = 1, 3, 5, 7
Number of odd numbers = 4.
P (Getting odd numbers) = 4/8 = ½.
Example 2: A bag contains only lemon-flavoured candies. Arjun takes out one candy without looking into the bag. What is the probability that he takes out an orange-flavoured candy?
Sol:
Let us take the number of candies in the bag to be 100.
Number of orange-flavoured candies = 0 [since the bag contains only lemon-flavoured candies]
Hence, the probability that he takes out an orange-flavoured candy is:
P (Taking orange-flavoured candy) = Number of orange-flavoured candies / Total number of candies.
= 0/100 = 0
Hence, the probability that Arjun takes out an orange-flavoured candy is zero.
This proves that the probability of an impossible event is 0.
|
123 videos|457 docs|77 tests
|

|
Explore Courses for Class 10 exam
|

|
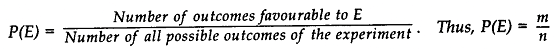
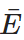 )
)