Surface Area and Volumes Class 9 Notes Maths Chapter 12
Plane Figures
The figures which we can draw on a piece of paper or which lie on a plane are called Plane Figures.
Example: Circle, Square, Rectangle etc.
Solid Figures
The 3D shapes which occupy some space are called Solid Figures.
Example - Cube, Cuboid, Sphere etc.

Volume
Space occupied by any solid shape is the capacity or volume of that figure. The unit of volume is a cubic unit.
Surface Area
The area of all the faces of the solid shape is the total surface area of that figure. The unit of surface area is a square unit.
Lateral or Curved Surface Area
The surface area of the solid shape after leaving the top and bottom face of the figure is called the lateral surface of the shape. The unit of lateral surface area is a square unit.
Surface Area and Volume of a Cube
Cube is a solid shape having 6 equal square faces.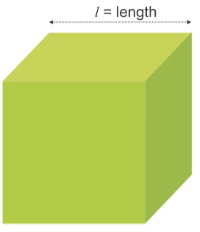

Example: What is the capacity of a cubical vessel having each side of 8 cm?
Sol:
Given side = 8 cm
So, Volume of the cubical vessel = l3
= (8)3 = 256 cm3.
Surface Area and Volume of a Cuboid
Cuboid is a solid shape having 6 rectangular faces at a right angle.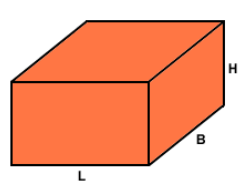

Example: What is the surface area of a cereal box whose length, breadth and height is 20 cm, 8 cm and 30 cm respectively?
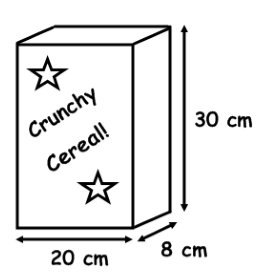
Sol:
Given,
Length = 20 cm
Breadth = 8 cm
Height = 30 cm
Total surface area of the cereal box = 2(lb + bh + lh)
= 2(20 × 8 + 8 × 30 + 20 × 30)
= 2(160 + 240 + 600)
= 2(1000) = 2000 cm2.
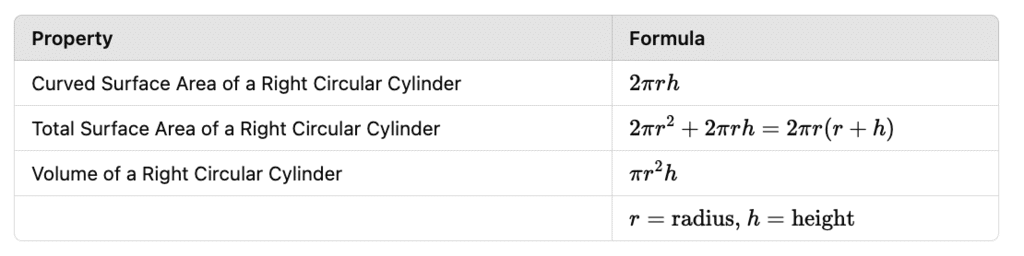
Surface Area and Volume of a Right Circular Cylinder
If we fold a rectangular sheet with one side as its axis then it forms a cylinder. It is the curved surface of the cylinder. And if this curved surface is covered by two parallel circular bases then it forms a right circular cylinder.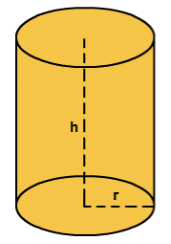
Surface Area and Volume of a Hollow Right Circular Cylinder
If a right circular cylinder is hollow from inside then it has different curved surface and volume.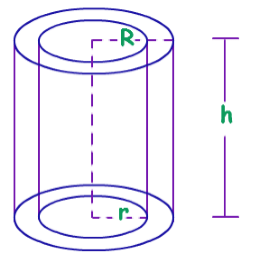
Curved surface area of a Right circular cylinder | 2πh (R + r) |
Total surface area of a Right circular cylinder | 2πh (R + r) + 2π(R2 - r2) |
R = outer radius, r = inner radius |
Example: Find the Total surface area of a hollow cylinder whose length is 22 cm and the external radius is 7 cm with 1 cm thickness. (π = 22/7)
Sol:
Given, h = 22 cm
R = 7 cm
r = 6 cm (thickness of the wall is 1 cm)
Total surface area of a hollow cylinder = 2πh(R + r) + 2π(R2 - r2)
= 2(π) (22) (7+6) + 2(π)(72 - 62)
= 572 π + 26 π = 598 π
= 1878.67 cm2
Surface Area and Volume of a Right Circular Cone
If we revolve a right-angled triangle about one of its sides by taking other as its axis then the solid shape formed is known as a Right Circular Cone.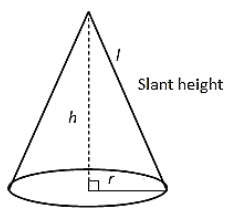

Surface Area and Volume of a Sphere
A sphere is a solid shape which is completely round like a ball. It has the same curved and total surface area.


Surface Area and Volume of a Hemisphere
If we cut the sphere in two parts then is said to be a hemisphere.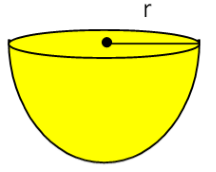
Curved or Lateral surface area of a Sphere | 2πr2 |
Total surface area of a Sphere | 3πr2 |
Volume of a Sphere | (2/3) πr3 |
r = radius |
Example: If we have a metal piece of cone shape with volume 523.33 cm3 and we mould it in a sphere then what will be the surface area of that sphere?
Solution: Given, volume of cone = 523.33 cm3
Volume of cone = Volume of Sphere
Volume of sphere = 100 π cm3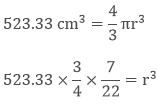
125 = r3
r = 5
Surface area of a sphere = 4πr2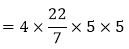
= 314.28 cm2.
|
40 videos|471 docs|57 tests
|





















