Mensuration Class 6 Notes Maths Chapter 9
Plane Figures
The closed 2-D shapes are referred to as plane figures.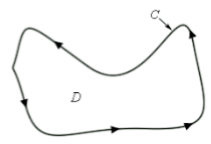
Here “C” is the boundary of the above figure and the area inside the boundary is the region of this figure. Point D comes in the area of the given figure.

Perimeter
- Perimeter refers to the length of the boundary of a closed figure.
- If a figure is made up of line segments only then we can find its perimeter by adding the length of all the sides of the given figure.
Example: Find the Perimeter of the given figure. Sol: Perimeter = Sum of all the sides
Sol: Perimeter = Sum of all the sides
= (12 + 3 + 7 + 6 + 10 + 3 + 15 + 12) m
= 68 m
Perimeter of Rectangle
A rectangle is a closed figure with two pairs of equal opposite sides.
Perimeter of a rectangle = Sum of all sides = length + breadth + length + breadth
Thus, Perimeter of a rectangle = 2 × (length + breadth)
Example : Find the cost of fencing a rectangular farm of length 24 meters and breadth 18 meters at 8/- per meter.
Sol: Perimeter of a rectangle = 2 × (length + breadth)
Perimeter of the farm = 2 × (24 + 18) = 2 × 42 = 84 meter
Cost of fencing = 84 × 8 = Rs. 672
Thus the cost of fencing the farm is Rs. 672/-.
[
Regular Closed Figure
- Figures with equal length of sides and an equal measure of angles are known as Regular Closed Figures or Regular Polygon.
- Perimeter of Regular Polygon = Number of sides × Length of one side
Perimeter of Square
Square is a regular polygon with 4 equal sides.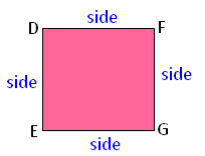
Perimeter of square = side + side + side + side
Thus, Perimeter of a square = 4 × length of a side
Example: Find the perimeter of a square having side length 25 cm.
Sol: Perimeter of a square = 4 × length of a side
Perimeter of square = 4 × 25 = 100 cm
Perimeter of an Equilateral Triangle
An equilateral triangle is a regular polygon with three equal sides and angles.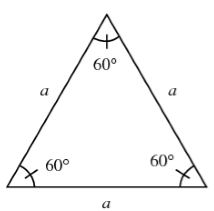 Perimeter of an equilateral triangle = 3 × length of a side
Perimeter of an equilateral triangle = 3 × length of a side
Example: Find the perimeter of a triangle having each side length 13 cm.
Sol: Perimeter of an equilateral triangle = 3 × length of a side
Perimeter of triangle = 3 × 13 = 39 cm
Perimeter of a Regular Pentagon
A regular pentagon is a polygon with 5 equal sides and angles.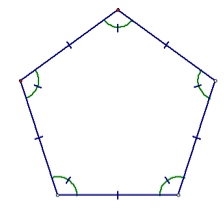
Perimeter of a regular pentagon = 5 × length of one side
Example: Find the perimeter of a pentagon having side length 9 cm.
Sol: Perimeter of a regular pentagon = 5 × length of one side
Perimeter of a regular pentagon = 5 × 9
= 45 cm
Perimeter of a Regular Hexagon
A regular hexagon is a polygon with 6 equal sides and angles.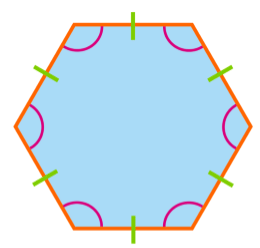 Perimeter of a regular hexagon = 6 × Length of one side
Perimeter of a regular hexagon = 6 × Length of one side
Example: Find the perimeter of a hexagon having side length 15cm.
Sol: Perimeter of a regular hexagon = 6 × Length of one side
Perimeter of a regular hexagon = 6 × 15
= 90 cm
Area
Area refers to the surface enclosed by a closed figure.
To find the area of any irregular closed figure, we can put them on a graph paper with the square of 1 cm × 1 cm .then estimate the area of that figure by counting the area of the squares covered by the figure. Here one square is taken as 1 sq.unit.
Example: Find the area of the given figure. (1 square = 1 m2)
Sol: The given figure is made up of line segments and is covered with some full squares and some half squares.
Full squares in figure = 32
Half squares in figure = 21
Area covered by full squares = 32 × 1 sq. unit = 32 sq. unit.
Area covered by half squares = 21 × (1/2) sq. unit. = 10.5 sq. unit.
Total area covered by figure = 32 + 10.5 = 42.5 sq. unit.
Area of a Rectangle
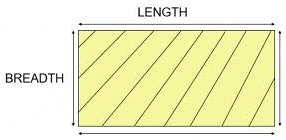
Area of a rectangle = (length × breadth)
Example: Find the area of a rectangle whose length and breadth are 20 cm and 12 cm respectively.
Sol: Length of the rectangle = 20 cm
Breadth of the rectangle = 12 cm
Area of the rectangle = length × breadth
= 20 cm × 12 cm
= 240 sq cm.
To find the length of a rectangle if breadth and area are given:
Area of a Square
Area of a square is the region covered by the boundary of a square.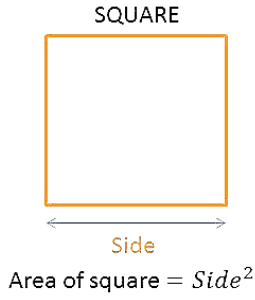
Area of a square = side × side
Example: Calculate the area of a square of side 13 cm.
Solution: Area of a square = side × side
= 13 × 13
= 169 cm2.
|
92 videos|348 docs|54 tests
|
FAQs on Mensuration Class 6 Notes Maths Chapter 9
| 1. What is the formula to calculate the perimeter of a rectangle? |  |
| 2. How do you find the perimeter of a square? |  |
| 3. What is the formula for the perimeter of an equilateral triangle? |  |
| 4. How can I calculate the area of a rectangle? |  |
| 5. What is the method to find the perimeter of a regular hexagon? |  |

|
Explore Courses for Class 6 exam
|

|



















