Rational Numbers Class 7 Notes Maths Chapter 1
Natural Numbers
 All positive integers like 1, 2, 3, 4……..are natural numbers.
All positive integers like 1, 2, 3, 4……..are natural numbers.
Whole Numbers
All natural numbers including 0 are whole numbers.
Integers
All negative and positive numbers including 0 are called Integers.
Rational Numbers
Rational Numbers are the numbers that can be expressed in the form p/q where p and q are integers (q ≠ 0). It includes all natural, whole numbers, fractions and integers.
Equivalent Rational Numbers
By multiplying or dividing the numerator and denominator of a rational number by the same integer, we can obtain another rational number equivalent to the given rational number. Numbers are said to be equivalent if they are proportionate to each other.
Example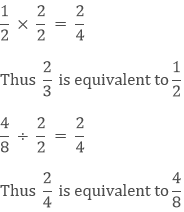
Therefore 1/2, 2/4, 4/8 are equivalent to each other as they are equal to each other.
Positive and Negative Rational Numbers
1. Positive Rational Numbers are the numbers whose both the numerator and denominator are positive.
Example: 3/4, 12/24 etc.
2. Negative Rational Numbers are the numbers whose one of the numerator or denominator is negative.
Example: (-2)/6, 36/(-3) etc.
Rational Numbers on the Number Line
Representation of whole numbers, natural numbers and integers on a number line is done as follows Rational Numbers can also be represented on a number line like integers i.e. positive rational numbers are on the right to 0 and negative rational numbers are on the left of 0.
Rational Numbers can also be represented on a number line like integers i.e. positive rational numbers are on the right to 0 and negative rational numbers are on the left of 0.
Representation of rational numbers can be done on a number line as follows
Rational Numbers in Standard Form
A rational number is in the standard form if its denominator is a positive integer and there is no common factor between the numerator and denominator other than 1.
If any given rational number is not in the standard form then we can reduce it to its standard form or the lowest form by dividing its numerator and denominator by their HCF ignoring its negative sign.
Example: Find the standard form of 12/18
Sol:
2/3 is the standard or simplest form of 12/18
Comparison of Rational Numbers
1. To compare the two positive rational numbers we need to make their denominator same, then we can easily compare them.
Example: Compare 4/5 and 3/8 and tell which one is greater.
Sol: To make their denominator same, we need to take the LCM of the denominator of both the numbers. LCM of 5 and 8 is 40.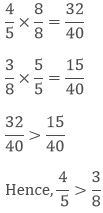
2. To compare two negative rational numbers, we compare them ignoring their negative signs and then reverse the order.
Example: Compare - (2/5) and – (3/7) and tell which one is greater.
Sol: To compare, we need to compare them as normal numbers.
LCM of 5 and 7 is 35.
by reversing the order of the numbers.
3. If we have to compare one negative and one positive rational number then it is clear that the positive rational number will always be greater as the positive rational number is on the right to 0 and the negative rational numbers are on the left of 0.
Example: Compare 2/5 and – (2/5) and tell which one is greater.
Sol: It is simply that 2/5 > - (2/5)
Rational Numbers between Rational Numbers
To find the rational numbers between two rational numbers, we have to make their denominator same then we can find the rational numbers.
Example: Find the rational numbers between 3/5 and 3/7.
Sol: To find the rational numbers between 3/5 and 3/7, we have to make their denominator same.
LCM of 5 and 7 is 35.
Hence the rational numbers between 3/5 and 3/7 are
These are not the only rational numbers between 3/5 and 3/7.
If we find the equivalent rational numbers of both 3/5 and 3/7 then we can find more rational numbers between them.
Hence we can find more rational numbers between 3/5 and 3/7.
Operations on Rational Numbers
1. Addition
(a) Addition of two rational numbers with the same denominator
i. We can add it using a number line.
Example: Add 1/5 and 2/5
Sol: On the number line we have to move right from 0 to 1/5 units and then move 2/5 units more to the right.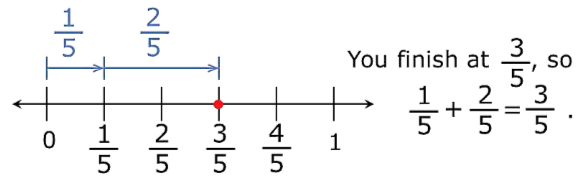 ii. If we have to add two rational numbers whose denominators are same then we simply add their numerators and the denominator remains the same.
ii. If we have to add two rational numbers whose denominators are same then we simply add their numerators and the denominator remains the same.
Example: Add 3/11 and 7/11.
Sol: As the denominator is the same, we can simply add their numerator.
(b) Addition of two Rational Numbers with different denominator
If we have to add two rational numbers with different denominators then we have to take the LCM of denominators and find their equivalent rational numbers with the LCM as the denominator, and then add them.
Example: Add 2/5 and 3/7.
Sol: To add the two rational numbers, first, we need to take the LCM of denominators the find the equivalent rational numbers.
LCM of 5 and 7 is 35.
(c) Additive Inverse
Like integers, the additive inverse of rational numbers is also the same.
a + (-a) = 0
This shows that the additive inverse of 3/7 is - (3/7)
This shows that
2. Subtraction
If we have to subtract two rational numbers then we have to add the additive inverse of the rational number that is being subtracted to the other rational number.
a - b = a + (-b)
Example: Subtract 4/21 from 8/21.
Sol: (i) In the first method, we will simply subtract the numerator and the denominator remains the same.
(ii) In the second method, we will add the additive inverse of the second number to the first number.
3. Multiplication
(a) Multiplication of a Rational Number with a Positive Integer.
To multiply a rational number with a positive integer we simply multiply the integer with the numerator and the denominator remains the same.
Example
(b) Multiply of a Rational Number with a Negative Integer
To multiply a rational number with a negative integer we simply multiply the integer with the numerator and the denominator remains the same and the resultant rational number will be a negative rational number.
Example
(c) Multiply of a Rational Number with another Rational Number
To multiply a rational number with another rational number we have to multiply the numerator of two rational numbers and multiply the denominator of the two rational numbers.
Example: Multiply 3/7 and 5/11.
Sol: 
4. Division
(a) Reciprocal
Reciprocal is the multiplier of the given rational number which gives the product of 1.
Reciprocal of a/b is b/a
Product of Reciprocal
If we multiply the reciprocal of the rational number with that rational number then the product will always be 1.
Example:
(b) Division of a Rational Number with another Rational Number
To divide a rational number with another rational number we have to multiply the reciprocal of the rational number with the other rational number.
Example: Divide
Sol:
|
76 videos|344 docs|39 tests
|
FAQs on Rational Numbers Class 7 Notes Maths Chapter 1
| 1. What are the differences between natural numbers, whole numbers, and integers? |  |
| 2. How can we identify equivalent rational numbers? |  |
| 3. How do we represent positive and negative rational numbers on the number line? |  |
| 4. What is the standard form of a rational number and how is it determined? |  |
| 5. How do we compare rational numbers and determine which is greater? |  |

|
Explore Courses for Class 7 exam
|

|


















