Important Questions: Statistics

Q1: Find the variance and the standard deviation for the following data: 57, 64, 43, 67, 49, 59, 44, 47, 61, 59.
Ans: Given data: 57, 64, 43, 67, 49, 59, 44, 47, 61, 59
To find mean (μ):
Mean (μ)= ( 57+ 64+ 43+ 67+ 49+ 59+ 44+ 47+ 61+ 59)/10
= 550/10
Mean = 55
To find Variance (σ²):
Variance(σ²) = (xi - μ)2/n
= (2² + 9² + 12² + 12² + 6² + 4² + 6² + 4² + 11² + 8²)/10
= 662/10
=66.2
Therefore, variance(σ2) = 66.2
To find standard deviation (σ):
To find the standard deviation, take the square root of variance, we get
Standard Deviation(σ) = √(σ²)
= √66.2 = 8.13
Therefore, the standard deviation is 8.13.

Q2: Find the mean deviation about mean for the following data:

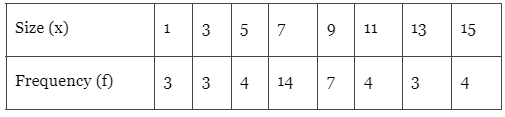
Ans: Let mean = μ
The formula to find mean is
μ = f_i x_i / N
N = 3+3+4+14+7+4+3+4 = 42
μ = (3+ 9+ 20+ 98+ 63+ 44+ 39+ 60)/42
μ = 336/42
μ = 8
Now, to find the mean deviation about mean:
The formula is:
M.D(μ) = fi |x_i- μ| / N
M.D(μ) =[3(7)+3(5)+ 4(3)+ 14(1)+7(1)+ 4(3)+ 3(5)+ 4(7)]/42
= (21+ 15+ 12+ 14+ 7+12+ 15+ 28)/42
= 62/21
= 2.95
Therefore, the mean deviation about mean for the given data is 2.95

Q3: The variance of the given data 2, 4, 5, 6, 8, 17 is 23.33. Then find the variance for the data 4, 8, 10, 12, 16, 34.
Ans: For the given data: 2, 4, 5, 6, 8, 17, the variance is 23.33.
To find the variance for the data: 4, 8, 10, 12, 16, 34
If you notice the data which you have to find the variance, it is the multiple of the given data.
So, multiply the variance of the given data by 2,
It means that, 23.33 x 2 = 46.66
Thus, the variance of the data: 4, 8, 10, 12, 16, 34 is 46.66

Q4: The coefficients of variations for the two distributions are 60 and 70 and its standard deviations are 21 and 16 respectively. Determine its arithmetic mean.
Ans: Given that,
Coefficient of Variations (C.V of 1st distribution) = 60, σ₁ = 21
Coefficient of Variations (C.V of 2nd distribution) = 70, σ₂ = 16
Let μ₁ and μ₂ are the means of the 1st and the 2nd distribution.
We know that the formula to find the arithmetic mean is given as:
Coefficient of Variations(C.V) = (Standard Deviation/arithmetic Mean) x 100
Thus, Arithmetic Mean = (Standard Deviation/C.V)x100
Therefore, the arithmetic mean for the 1st deviation is given by:
μ₁= [σ₁ / (c.v of 1st distribution)] x100
μ₁= (21/60)x100
μ₁= 0.35×100
μ₁= 35
Similarly for μ₂:
μ₂ = [σ₂ / (c.v of 2nd distribution)]x100
μ₂ = (16/70)x100
μ₂ = 0.2285×100
μ₂ = 22.85
Therefore, the arithmetic mean for the 1st and the 2nd distributions are 35 and 22.85 respectively.

Q5: Determine the mean deviation about the median for the following data: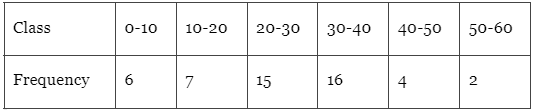
Ans: From the given data: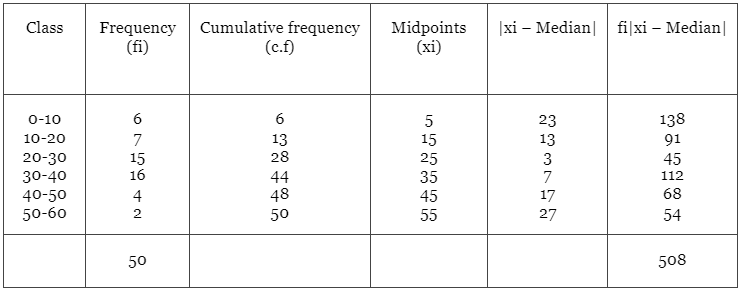

From this, it is noticed that the class interval containing 25th item is 20-30. Therefore, the median is 20-30.
We know that the formula for the median is given as:
Median = l+ {[((N/2)-C)/f] x h}
Here l = 20, f = 15, C=13, N = 50, and h = 10
Now substitute these values in the formula, we get:
Median = 20+ {[(25-13)/15] x 10}
= 20+8
= 28
Therefore, median is 28.
Hence, the mean deviation about the median is given by:
M.D(M)=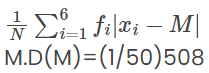

M.D(M) = 10.16
Hence, the mean deviation about the median is 10.16.