Arithmetic Reasoning Tips and Tricks for Government Exams
| Table of contents |

|
| Introduction |

|
| Arithmetic Reasoning Formulas |

|
| Types of Arithmetic Reasoning |

|
| Arithmetic Reasoning Tips and Tricks |

|
| Examples |

|
Introduction
Arithmetic Reasoning is the ability to understand and solve mathematical problems using basic arithmetic operations such as addition, subtraction, multiplication, and division. This skill involves the application of logic, critical thinking, and problem-solving techniques to perform calculations and analyze numerical relationships. It is an essential component of mathematics education and is crucial for everyday tasks, as well as more complex activities such as financial management, engineering, and scientific research. Arithmetic reasoning is not only about the ability to perform calculations but also about understanding the underlying concepts, recognizing patterns, and making informed decisions based on numerical data.
Arithmetic Reasoning Formulas
Arithmetic reasoning often involves using basic formulas to solve problems.
Here's a list of some common arithmetic formulas that can be helpful:
- Addition: a + b = c
- Subtraction: a - b = c
- Multiplication: a * b = c
- Division: a / b = c
- Average: (a + b + c + ... + n) / n
- Percentage: (part/whole) * 100
- Ratio: a : b
- Proportion: a / b = c / d
- Distance: Speed * Time
- Speed: Distance / Time
- Time: Distance / Speed
- Simple Interest: I = P * R * T / 100 (where I = interest, P = principal, R = rate, and T = time)
- Compound Interest: A = P(1 + r/n)^(nt) (where A = amount, P = principal, r = annual interest rate, n = number of times interest is compounded per year, and t = time in years)
- Profit or Loss: Profit = Selling Price - Cost Price (Loss = Cost Price - Selling Price)
- Percent Increase or Decrease: (New Value - Old Value) / Old Value * 100
- Fractions:
- Addition: a/b + c/d = (ad + bc) / bd
- Subtraction: a/b - c/d = (ad - bc) / bd
- Multiplication: (a/b) * (c/d) = (a * c) / (b * d)
- Division: (a/b) ÷ (c/d) = (a * d) / (b * c)
- Decimal to Fraction: To convert a decimal to a fraction, write the decimal as the numerator and the denominator as a power of 10 based on the number of decimal places. Then, simplify the fraction.
- Fraction to Decimal: Divide the numerator by the denominator.
- Fraction to Percentage: (Fraction) * 100
- Percentage to Fraction: (Percentage) / 100
- Percentage to Decimal: (Percentage) / 100
- Decimal to Percentage: (Decimal) * 100
- Weighted Average: (w1 * x1 + w2 * x2 + ... + wn * xn) / (w1 + w2 + ... + wn)
- Least Common Multiple (LCM): The smallest multiple that is exactly divisible by each of the numbers.
- Greatest Common Divisor (GCD): The largest number that divides two or more numbers without leaving a remainder.
- Prime Numbers: A number greater than 1 that has only two factors: 1 and itself.
- Factors: The numbers that can be multiplied together to get the original number.
- Square of a Number: a² = a * a
- Cube of a Number: a³ = a * a * a
- Square Root: √a is the number that, when multiplied by itself, equals a.
- Cube Root: ∛a is the number that, when multiplied by itself three times, equals a.
- Permutations: nPr = n! / (n - r)!, where n is the total number of elements and r is the number of elements chosen.
- Combinations: nCr = n! / [r!(n - r)!], where n is the total number of elements and r is the number of elements chosen.
These arithmetic formulas cover the basic concepts and can be applied to various problem-solving situations. However, keep in mind that more advanced arithmetic problems might require additional formulas or a combination of these basic formulas.
Types of Arithmetic Reasoning
- Puzzle: In these type of arithmetic reasoning questions, candidates need to analyze the given piece of information, pick the information that is important, and leave out the information that is not required in solving the given set of questions.
- Analogy: In these type of arithmetic reasoning questions, candidates will need to find a word or paid words analogous to those given in the question.
- Series: In these type of arithmetic reasoning questions, Candidates need to find the missing or wrong number in the provided series. There may be some questions where one of the terms in the given series will be incorrect, and candidates need to find out that term of the series by identifying the pattern involved in the formation of the series.
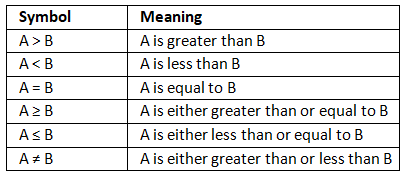
- Inequality: In these type of arithmetic reasoning questions, candidates must know about various signs, which are used in such types of questions. The same is given below:

- Venn Diagram: A Venn Diagram is a representation method for all possible relations that can exist between a given group of elements in a single figure. A venn diagram is the easiest way to express the relationship between sets.
- Cube & Dice: In these type of arithmetic reasoning questions, problems based on single or multiple cube and dice will be asked and candidates need to give the correct answer by analyzing the given image.
Arithmetic Reasoning Tips and Tricks
Solving arithmetic reasoning questions can be made easier by following a step-by-step approach. Here are some arithmetic reasoning tricks and tips to help you tackle these problems more effectively:
- Read the question carefully: Make sure you thoroughly understand the problem statement of the arithmetic reasoning question and identify the information given, as well as what you need to find out.
- Break down the problem: Simplify complex arithmetic problems by breaking them into smaller, more manageable parts. Identify the underlying concepts and relationships between the given data.
- Choose the right formula or method: Based on the information and relationships identified, select the appropriate arithmetic formula or method to solve the problem.
- Organize the data: Arrange the given data and any additional information you've deduced in a structured way. This can be in the form of a table, diagram, or equation.
- Perform calculations: Apply the chosen arithmetic formula or method and carry out the necessary calculations. Keep track of units, if applicable, and ensure the accuracy of your calculations.
- Check your work: Verify the accuracy of your calculations and ensure that your answer makes logical sense in the context of the problem. If necessary, retrace your steps and identify any errors.
- Simplify the answer: If required, simplify your answer by expressing it in the most appropriate format, such as a fraction, decimal, or percentage.
- Review the question: Go back to the problem statement and ensure your answer addresses what was asked. If the question has multiple parts, make sure you've addressed all aspects.
Examples
Example 1: A store sells packs of 6 pens for $4.50 per pack. How much would 3 packs cost?
Ans: Cost of 3 packs = 3 * $4.50 = $13.50
Example 2: If a square has a side length of 8 units, what is the length of its diagonal?
Ans: Diagonal length = Side length * √2 Diagonal length = 8 * √2 = 8√2 units
Example 3: What is the average of the numbers 18, 24, and 30?
Ans: Average = (Sum of numbers) / (Number of numbers)
Average = (18 + 24 + 30) / 3
Average = 72 / 3 = 24
Example 4: If 9 books weigh 36 pounds, how much would 15 books weigh?
Ans: Weight of 1 book = 36 pounds / 9 books = 4 pounds/book
Weight of 15 books = 15 books * 4 pounds/book = 60 pounds
Example 5: A car rental company charges $20 per day plus an additional $0.15 per mile driven. How much would it cost to rent a car for 3 days and drive 200 miles?
Ans: Cost for 3 days = 3 * $20 = $60
Cost for 200 miles = 200 * $0.15 = $30
Total cost = $60 + $30 = $90
Example 6: Solve the following equation: 5(x - 3) = 4(x + 2)
Ans: 5(x - 3) = 4(x + 2)
5x - 15 = 4x + 8
5x - 4x = 15 + 8 x = 23
Example 7: A fruit seller sold 120 kg of apples at $4 per kg and 80 kg of oranges at $5 per kg. How much money did he earn in total?
Ans: Money from apples = 120 kg * $4 = $480
Money from oranges = 80 kg * $5 = $400
Total money earned = $480 + $400 = $880
Example 8: If the sum of three consecutive even numbers is 78, what is the largest number?
Ans: Let the numbers be x, x + 2, and x + 4.
x + (x + 2) + (x + 4) = 78
3x + 6 = 78 3x = 72 x = 24
The largest number is x + 4 = 24 + 4 = 28
Example 9: A rectangular garden has a perimeter of 60 meters, and its width is 10 meters. What is its length?
Ans: Perimeter of a rectangle = 2 * (length + width)
60 = 2 * (length + 10)
30 = length + 10
Length = 20 meters
Example 10: What is the sum of the first ten positive odd numbers?
Ans: The first ten positive odd numbers are: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Sum = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100
|
1365 videos|1312 docs|1010 tests
|
|
1365 videos|1312 docs|1010 tests
|

|
Explore Courses for SSC CGL exam
|

|