Counting Figures Tips and Tricks for Government Exams
How to Calculate Number of Triangles in a Shape: Trick to Count No of Triangles
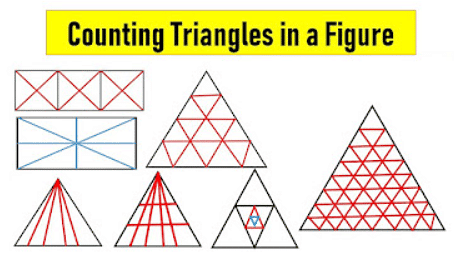
Calculate the number of triangles in a square
Type – 1: Counting triangles with in Square, Rectangle, Quadrilateral

Find the number of triangles in the above figures
Figure – 1: Number of triangles in Fig – 1 = 8
Hint: Here having total two diagonals and having four blocks. So formula for that 4 x 2 = 8 number of triangles.
Figure – 2: Number of triangles in Fig – 2 = 16
Hint: Here having total two diagonals and having eight blocks. So formula for that 8 x 2 = 16 number of triangles.
Figure – 3: Number of triangles in Fig – 3 = 18
Hint: Here each square having 8 no. of triangles and combine squares having 2 no. of triangles. So total number of triangles – 8 + 8 + 2 = 18.
Figure – 4: Number of triangles in Fig – 3 = 28
Hint: Here each square having 8 no. of triangles and combine squares having 4 no. of triangles. So total number of triangles – 8 + 8 + 8 + 4 = 28.
Trick to count no of triangles: Intersection of diagonals in a square, rectangle, rhombus, parallelogram, quadrilateral and trapezium will give eight triangles.
Type – 2: Counting triangles with the Triangle having number of bisects with vertex
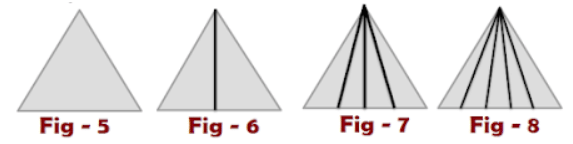
Count the number of possible triangles in the above figures.
Figure – 5: Number of possible triangles in Fig – 5 = 1
Figure – 6: Number of possible triangles in Fig – 6 = 3
Formula: Here number of parts ” n” then possible triangles is n (n+1) /2
Figure – 7: Number of possible triangles in Fig – 7 = 10
Hint: No of parts ” n” = 4 so according to formula 4 x 5 /2 = 10
Figure – 8: Number of possible triangles in Fig – 8 = 15
Hint: No of parts ” n” = 5 so according to formula 5 x 6 /2 = 15.
Type – 3: Counting triangles with the Triangle having number of bisects with vertex and horizontal lines
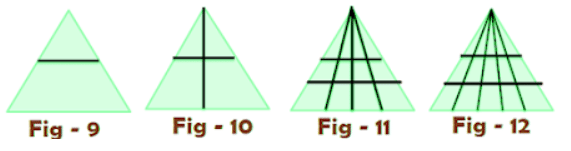
Count the number of triangles in the above picture.
Figure – 9: Triangle counting in Fig – 9 = 2
Figure – 10: Triangle counting in Fig – 10 = 6
Formula: Here number of vertical parts ” n” and horizontal parts “m” then possible triangles is
{n × m × (n + 1)}/2
Figure – 11: Triangle counting in Fig – 11 = 30
Ans: Here number of vertical parts ” 4″ and horizontal parts “3” then possible triangles is 4 x 3 x 5 /2 = 30
Figure – 12: Triangle counting in Fig – 12 = 45
Ans: Here number of vertical parts ” 5″ and horizontal parts “3” then possible triangles is 5 x 3 x 6 /2 = 45
Type – 4: Counting triangles within embedded Triangle

How many triangles are in the above figures?
Figure – 13: Triangle counting in Fig – 13 = 5
Formula: Here number embedded triangles in outer triangle ” n” and horizontal parts “m” then possible triangles is 4n + 1
Figure – 14: Triangle counting in Fig – 14 = 9 ( Here n = 2 )
Figure – 15: Triangle counting in Fig – 15 = 13 ( Here n = 3 )
Type – 5: Counting triangles with in the particular pattern of Triangle

How many possible triangles are in the above figures?
Formula to count number of triangles like above particular pattern type of Triangle
{n(n + 2)(2n + 1)}/8 where “n” = number of unit triangles in a side
Remark: Consider only integer part from answer obtained in above formula ( For example the answer may come 13.12 then consider only “13”. Also remember You don’t have to round off the number for example answer may come 36.8 then consider only “36”.
Figure – 16: No of triangles in Fig – 16 = 13 ( Here n = 3 )
Ans: According to above formula 3 x 5 x 7 /8 = 13.12 so consider integer only i.e 13
Figure – 17: No of triangles in Fig – 17 = 27 ( Here n = 4 )
Ans: According to above formula 4 x 6 x 9/8 = 27
Figure – 18: No of triangles in Fig – 18 = 170 ( Here n = 8 )
Ans: According to above formula 8 x 10 x 17/8 = 170
|
1334 videos|1437 docs|834 tests
|
















