Important Derivations: Moving Charges and Magnetism | Physics Class 12 - NEET PDF Download
(1) Biot Savarts Law
With the help of experimental results, Biot and Savart arrived at a mathematical expression that gives
the magnetic field at some point in space in terms of the current that produces the field.
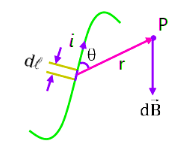
Experimentally, it was found that, magnetic field at point P varies as:
(1)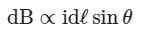 (2)
(2)
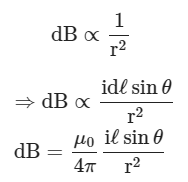
here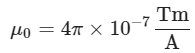 (permeability of free space)
(permeability of free space)
Unit of B: T or Wb/m2
Scalar Form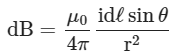
Vector Form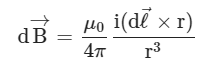
(2) The parallel coaxial circular coils of equal radius R and equal number of turns N carry equal currents I in the same direction and are separated by a distance 2 R. Find the magnitude and direction of the net magnetic field produced at the mid-point of the line joining their centres.
To find the magnitude and direction of the net magnetic field at the midpoint of the line joining the centers of two parallel coaxial circular coils, we can use the principle of superposition.
Let’s consider the two circular coils, Coil 1 and Coil 2, carrying equal currents I in the same direction. They have equal radii R and are separated by a distance of 2R. The midpoint of the line joining their centers is the point where we want to find the net magnetic field.
At the midpoint, the magnetic field produced by Coil 1 and Coil 2 will add together to give the net magnetic field.
The magnetic field (B1) produced at the midpoint due to Coil 1 can be calculated using the formula for the magnetic field at the center of a circular coil: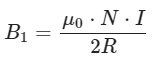
where: μ0 = Permeability of free space (4π×10−7T⋅m/A),
N = Number of turns in each coil (since they have equal turns, N is the same for both coils),
I = Current flowing through each coil,
R = Radius of each coil.
The magnetic field (B2) produced at the midpoint due to Coil 2 is the same as B1 since both coils are identical and carry the same current.
Now, to find the net magnetic field (Bnet) at the midpoint, we add the contributions from both coils:
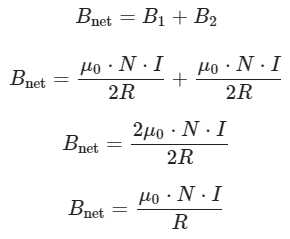
So, the magnitude of the net magnetic field at the midpoint is 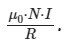 The direction of the net magnetic field is along the axis of the coils, which is the line joining their centers. It points from Coil 1 to Coil 2.
The direction of the net magnetic field is along the axis of the coils, which is the line joining their centers. It points from Coil 1 to Coil 2.
Therefore, the magnitude of the net magnetic field is 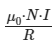 and its direction is along the axis of the coils from Coil 1 to Coil 2.
and its direction is along the axis of the coils from Coil 1 to Coil 2.
|
74 videos|314 docs|88 tests
|
FAQs on Important Derivations: Moving Charges and Magnetism - Physics Class 12 - NEET
| 1. What is the formula to calculate the magnetic field due to a long straight wire? |  |
| 2. How can the direction of the magnetic field due to a current-carrying wire be determined? |  |
| 3. What is Ampere's circuital law? |  |
| 4. Explain the working principle of a cyclotron. |  |
| 5. What is the force experienced by a current-carrying conductor placed in a magnetic field? |  |
















