Class 9 Maths Chapter 5 Previous Year Questions - Introduction to Euclid`s Geometry
Very Short Answer Type Questions
Q1. What is the Euclid’s fifth postulate?
 View Answer
View AnswerSol: It states that: “If a straight line falling on two straight lines make the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on the side on which the sum of the angles is less than two right angles.”
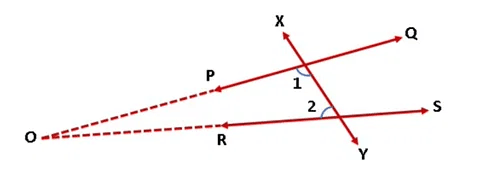
Q2. Which of the following are the boundaries of a surface: lines; curves; surfaces?
 View Answer
View AnswerSol: The boundaries of a surface are curves.
Q3. Johan is of the same age as Mohan. Raghu is also of the same age as Mohan. State Euclid’s axiom that illustrate the relative ages of Johan and Raghu.
 View Answer
View AnswerSol: The first axiom explains the above statement.
Q4. Which of the following is the 5th postulate of Euclid?
(i) The whole is greater than the part.
(ii) If a straight line falling on two straight lines make the interior angles on the same side of it taken together less than two right angles then the two straight lines if produced indefinitely meet on that side on which the sum of angles is less than two right angles.
(iii)“all right angles are equal to one another.”
 View Answer
View AnswerSol: The option (ii) is the Euclid’s fifth postulate.
Q5. Which of the following are assumed as axioms?
(i) Universal Truths in all branches of Mathematics.
(ii) Universal Truths specific to geometry.
(iii) Theorems
(iv) Definitions.
 View Answer
View AnswerSol: (i) The universal truths in all branches of Mathematics.
Q6. Complete the following statement: Pythagoras was a student of ................................... .
 View Answer
View AnswerSol: Pythagoras was the student of ‘Thales’.
Q7. What do we call a closed figure formed by three line segments
 View Answer
View AnswerSol: A triangle.
Q8. What do we call a figure formed by two straight lines having a common point?
 View Answer
View AnswerSol: An angle.
Short Answer Type Questions
Q1: In figure, it is given that AD=BC. By which Euclid’s axiom it can be proved that AC = BD?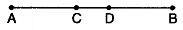
 View Answer
View AnswerSol:
We can prove it by Euclid’s axiom 3. “If equals are subtracted from equals, the remainders are equal.”
We have AD = BC
⇒ AD – CD = BC – CD
⇒ AC = BD
Q2: In the beow figure, if AB = PQ, PQ = XY, then AB = XY. State True or False. Justify your answer.
 View Answer
View AnswerSol:
True.
∵ By Euclid’s first axiom “Things which are equal to the same thing are equal to one another”.
∴ AB = PQ and XY = PQ ⇒ AB = XY
Q3: In the given figure, AC = XD, C is mid-point of AB and D is mid-point of XY. Using an Euclid’s axiom, show that AB = XY.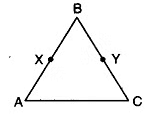
 View Answer
View AnswerSol:
∵ C is the mid-point of AB
AB = 2AC
Also, D is the mid-point of XY
XY = 2XD
By Euclid’s sixth axiom “Things which are double of same things are equal to one another.”
∴ AC = XD = 2AC = 2XD
⇒ AB = XY
Q4: In the given figure, if ∠1 = ∠3, ∠2 = ∠4 and ∠3 = ∠4, write the relation between ∠1 and ∠2, using an Euclid’s axiom.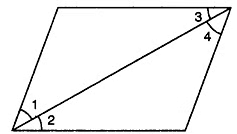
 View Answer
View AnswerSol:
Here, ∠3 = ∠4, ∠1 = ∠3 and ∠2 = ∠4. Euclid’s first axiom says, the things which are equal to equal thing are equal to one another. So ∠1 = ∠2.,
Q5: In the given figure, AB = BC, BX = BY, show that AX = CY.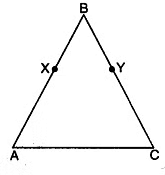
 View Answer
View AnswerSol:
Given that AB = BC and BX = BY
By using Euclid’s axiom 3, equals subtracted from equals, then the remainders are equal, we have
AB – BX = BC – BY
AX = CY
Q6: In the given figure, AC = DC and CB = CE. Show that AB = DE. Write the Euclid’s axiom to support this.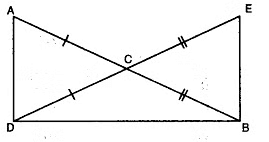
 View Answer
View AnswerSol:
We have
AC = DC
CB = CE
By using Euclid’s axiom 2, if equals are added to equals, then wholes are equal.
⇒ AC + CB = DC + CE
⇒ AB = DE.
Q7: If A, B and C are any three points on a line and B lies between A and C (see figure), then prove that AB + BC = AC.
 View Answer
View AnswerSol:
In the given figure, AC coincides with AB + BC. Also, Euclid’s axiom 4, states that things which coincide with one another are equal to one another. So, it is evident that:
AB + BC = AC.
Long Answer Type Questions
Q1: Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
(i) Parallel lines
 View Answer
View AnswerSol:
Two lines are said to be parallel, when the perpendicular distance between these lines is always constant or we can say that the lines that never intersect each other are called as parallel lines.

We need to define line first, in order to define parallel lines.
(ii) Perpendicular lines
 View Answer
View AnswerAns: Two lines are said to be perpendicular lines, when angle between these two lines is 90∘.

We need to define line and angle, in order to define perpendicular lines.
(iii) Line segment
 View Answer
View AnswerSol:
A line of a fixed dimension between two given points is called as a line segment.

We need to define line and point, in order to define a line segment.
(iv) Radius of a circle
 View Answer
View AnswerSol:
The distance of any point lying on the boundary of a circle from the center of the circle is called as radius of a circle.
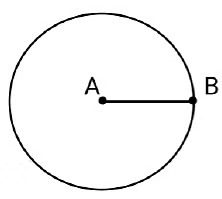
We need to define circle and center of a circle, in order to define radius of a circle.
(v) Square
 View Answer
View AnswerSol:
A quadrilateral with all four sides equal and all four angles of 90∘ is called as a square.
We need to define quadrilateral and angle, in order to define a square.
Q2: If a point C lies between two points A and B such that AC = BC, then prove that AC = 1/2AB⋅ Explain by drawing the figure.
 View Answer
View AnswerSol:
We are given that a point C lies between two points B and C, such that AC = BC.
We need to prove that AC = 1/2AB⋅
Let us consider the given below figure.

We are given that AC = BC−…(i)
An axiom of the Euclid says that "If equals are added to equals, the wholes are equal."
Let us add AC to both sides of equation (i).
AC + AC = BC + AC.
An axiom of the Euclid says that "Things which coincide with one another are equal to one another." "
We can conclude that BC+AC coincide with AB, or
AB = BC + AC.…(ii)
An axiom of the Euclid says that "Things which are equal to the same thing are equal to one another."
From equations (i) and (ii), we can conclude that
AC + AC = AB, or 2AC = AB
An axiom of the Euclid says that "Things which are halves of the same things are equal to one another."
Therefore, we can conclude that AC = 1/2AB
Q3: In the following figure, if AC = BD, then prove that AB = CD.
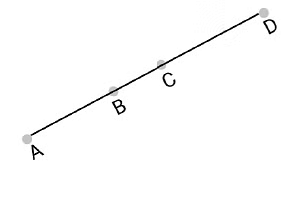
 View Answer
View AnswerSol:
We are given that AC = BD
We need to prove that AB = CD in the figure given below.

From the figure, we can conclude that
AC = AB + BC, and BD = CD + BC.
An axiom of the Euclid says that "Things which are equal to the same thing are equal to one another."
AB + BC = CD + BC
An axiom of the Euclid says that "when equals are subtracted from equals, the remainders are also equal."
We need to subtract BC from equation(i) to get AB + BC − BC = CD + BC− BC
AB = CD
Therefore, we can conclude that the desired result is proved.
Q4: How would you rewrite Euclid's fifth postulate so that it would be easier to understand?
 View Answer
View AnswerSol:
We need to rewrite Euclid's fifth postulate so that it is easier to understand.
We know that Euclid's fifth postulate states that "No intersection of lines will take place when the sum of the measures of the interior angles on the same side of the falling line is exactly 180∘.
We know that Playfair's axiom states that "For every line l and for every point P not lying on 1, there exists a unique line m passing through P and parallel to Γ.
The above mentioned Playfair's axiom is easier to understand in comparison to the Euclid's fifth postulate.
Let us consider a line l that passes through a point p and another line m. Let these lines be at a same plane.
Let us consider the perpendicular CD on l and FE on m.
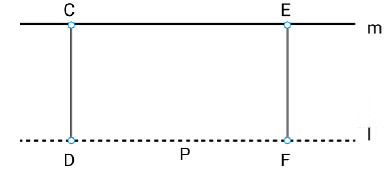
From the above figure, we can conclude that CD = EF.
Therefore, we can conclude that the perpendicular distance between lines m and l will b. constant throughout, and the lines m and l will never meet each other or in other words, w can say that the lines m and I are equidistant from each other.
Q5: Consider the two 'postulates' given below:
(i) Given any two distinct points A and B, there exists a third point C, which is between A and B.
(ii) There exists at least three points that are not on the same line. Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid's postulates?
Explain.
 View Answer
View AnswerSol:
Given any two distinct points A and B, there exists a third point C, which is between A and B.
There exists at least three points that are not on the same line. The undefined terms in the given postulates are point and line. The two given postulates are consistent, as they do not refer to similar situations and they refer to two different situations. We can also conclude that, it is impossible to derive at any conclusion or any statement that contradicts any well-known axiom and postulate.
The two given postulates do not follow from the postulates given by Euclid. The two given postulates can be observed following from the axiom, "Given two distinct points, there is a unique line that passes through them"
|
44 videos|412 docs|55 tests
|
FAQs on Class 9 Maths Chapter 5 Previous Year Questions - Introduction to Euclid`s Geometry
| 1. What is Euclid's Geometry? |  |
| 2. What are the basic elements of Euclid's Geometry? |  |
| 3. How is Euclid's Geometry relevant in modern mathematics? |  |
| 4. What are some key theorems in Euclid's Geometry? |  |
| 5. How did Euclid's Geometry influence the development of mathematics? |  |

|
Explore Courses for Class 9 exam
|

|

















