Class 9 Maths Chapter 8 Previous Year Questions - Quadrilaterals
Very Short Answer Type Questions
Q1. One angle of a quadrilateral is 140° and other three angles are in the ratio of 3 : 3 : 2. Find the measure of the smallest angle of the quadrilateral.
 View Answer
View Answer 
Sol:
Given: one of the angles = 140°
Remaining three angles = 360° - 140° = 220°
Ratio is 3 : 3 : 2
Let other angles be 3x, 3x, and 2x
Sum of all angles of quad is = 360 °
140° + 3x + 3x +2x = 360 °
8x = 360 ° - 140 °
8x = 220°
x = 220°/8
27.5°
All the angles will be 3x = 82.5°, 3x = 82.5°, and 2x= 55°
Hence, smallest angle out of all is 2x= 55°
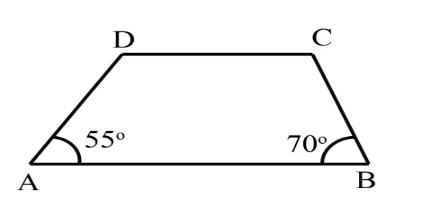
Q2.In the adjoining figure, ABCD is a trapezium in which AB II DC. If ∠A=55° and ∠B=70°, find ∠C and ∠D.
 View Answer
View Answer 
Sol: AB || DC and AD is a transversal.
∠A + ∠D = 180°
55°+ ∠D = 180°
∠D = 180°-55°
∠D = 125°
also,
∠B + ∠C = 180°
70° + ∠C = 180 °
∠C = 180° -70°
= 110°
Short Answer Type Questions
Q1. ABCD is a parallelogram in which AB = 4.5 cm, then find other sides of the parallelogram when its perimeter is 21 cm.
 View Answer
View Answer 
Sol:
∵ Opposite sides of a parallelogram are equal.
∴ AB = CD = 4.5 cm, and BC = AD
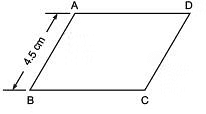
Now, AB + CD + BC + AD = 21 cm
⇒ AB + AB + BC + BC = 21 cm
⇒2[AB + BC] = 21 cm
⇒ 2[4.5 cm + BC] = 21 cm
⇒ [4.5 cm + BC] = (21/2)= 10.5 cm
⇒ BC = 10.5 - 4.5 = 6 cm
Thus, BC = 6 cm, CD = 4.5 cm and AD = 6 cm.
Q2. In a parallelogram ABCD, if (3x - 10)° = ∠ B and (2x + 10)° = ∠ C, then find the value of x.
 View Answer
View Answer 
Sol:
Since, the adjacent angles of a parallelogram are supplementary.
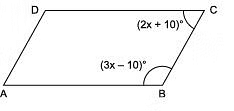
∴ ∠ B + ∠ C = 180° ( adjacent angles )
⇒ (3x - 10)° + (2x + 10)° = 180°
⇒ 3x + 2x - 10° + 10° = 180°
⇒ 5x = 180°
⇒ x= (180°/5)= 36°
Thus, the required value of x is 36°.
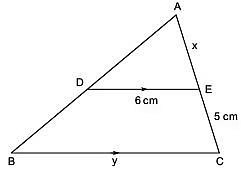
Q3. In the figure, D is the mid-point of AB and DE || BC. Find x and y.
 View Answer
View Answer 
Sol:
Since DE || BC and D is the mid-point of AB.
∴ E must be the mid-point of AC.
∴ AE = EC ⇒ x = 5 cm
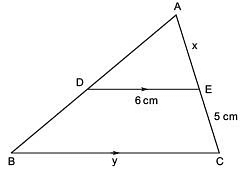
Also, DE || BC
⇒ DE = (1/2)BC (using mid point theorem )
⇒ 2DE = BC
⇒ 2 x 6 cm = BC
⇒ BC = 12 cm
⇒ y = 12 cm
Thus, x = 5 cm and y = 12 cm
Q4. E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = 1/2 (AB + CD) [Hint: Join BE and produce it to meet CD produced at G.]
 View Answer
View Answer 
Sol:
Given, ABCD is a trapezium in which AB || CD
E and F are the midpoints of the non-parallel sides AD and BC
We have to prove that EF || AB and EF = 1/2 (AB + CD)
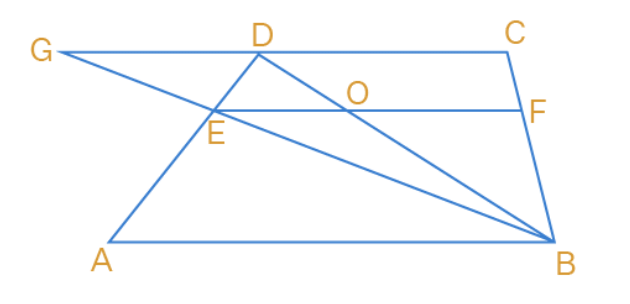
Construction: Join BE and extend it to meet CD produced at G
Draw BD which intersects EF at O.
Consider triangle GCB,
E and F are the midpoints of BG and BC.
By Midpoint theorem,
EF || GC
Given, AB || GC or CD || AB
So, EF || AB
Considering triangle ABD,
AB || EO
E is the midpoint of AD
By converse of midpoint theorem,
O is the midpoint of BD
EO = 1/2 AB -------------- (1)
Considering triangle BDC,
OF || CD
O is the midpoint of BD
By converse of midpoint theorem,
OF = 1/2 CD ------------- (2)
Adding (1) and (2),
EO + OF = 1/2 AB + 1/2 CD
From the figure,
EF = EO + OF
Therefore, EF = 1/2 (AB + CD)
Q5. In a quadrilateral, ∠ A : ∠ B : ∠ C : ∠ D = 1 : 2 : 3 : 4, then find the measure of each angle of the quadrilateral.
 View Answer
View Answer 
Sol:
Since ∠ A : ∠ B : ∠ C : ∠ D = 1 : 2 : 3 : 4
∴ If ∠ A = x, then ∠ B = 2x, ∠ C = 3x and ∠ D = 4x. ∴ ∠ A + ∠ B + ∠ C + ∠ D = 360°
⇒ x + 2x + 3x + 4x = 360° ⇒ 10x = 36°
⇒ x= (360°/10)= 36°
Therefore measure of all the angles are :
∠ A = x = 36°
∠ B = 2x = 2 x 36° = 72°
∠ C = 3x = 3 x 36° = 108°
∠ D = 4x = 4 x 36° = 144°
Long Answer Type Questions
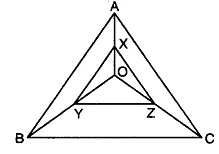
Q1: In ΔABC, AB = 8 cm, BC = 9 cm and AC = 10 cm. X, Y and Z are mid-points of AO, BO and CO respectively as shown in the figure. Find the lengths of the sides of ΔXYZ.
 View Answer
View Answer 
Sol:
Here, in ΔABC, AB = 8 cm, BC = 9 cm, AC = 10 cm.
In ΔAOB, X and Y are the mid-points of AO and BO.
∴ By using mid-point theorem, we have
XY = 1/2 AB = 1/2 x 8 cm = 4 cm
Similarly, in Δ BOC, Y and Z are the mid-points of BO and CO.
∴ By using mid-point theorem, we have
YZ = 1/2 BC = 1/2 x 9cm = 4.5 cm
And, in ΔCOA, Z and X are the mid-points of CO and AO.
∴ ZX = 1/2 AC = 1/2 x 10 cm = 5 cm
Hence, the lengths of the sides of ΔXYZ are XY = 4 cm, YZ = 4.5 cm and ZX = 5 cm.
Q2: In the figure, ABCD is a trapezium in which AB || DC. E and F are the mid-points of AD and BC respectively. DF and AB are produced to meet at G. Also, AC and EF intersect at the point O. Show that :
(i) EO || AB
(ii) AO = CO

 View Answer
View Answer 
Sol:
Here, E and F are the mid-points of AD and BC respectively.
In ΔBFG and ΔCFD
BF = CF [given]
∠BFG = ∠CFD (vert. opp. ∠s]
∠BGF = ∠CDF (alt. int. ∠s, as AB || DC)
So, by using AAS congruence axiom, we have
ΔBFG ≅ ΔCFD
⇒ DF = FG [c.p.c.t.)
Now, in ΔAGD, E and F are the mid-points of AD and GD.
∴ By mid-point theorem, we have
EF || AG
or EO || AB
Also, in ΔADC, EO || DC
∴ EO is a line segment from mid-point of one side parallel to another side.
Thus, it bisects the third side.
Hence, AO = CO
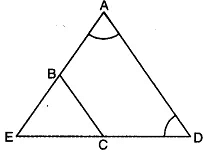
Q3: In the given figure, AE = DE and BC || AD. Prove that the points A, B, C and D are concyclic. Also, prove that the diagonals of the quadrilateral ABCD are equal.
 View Answer
View Answer 
Sol:
Since AE = DE
∠D = ∠A …. (i) [∵ ∠s opp. to equal sides of a Δ]
Again, BC || AD
∠EBC = ∠A …. (ii) (corresponding ∠s]
From (i) and (ii), we have
∠D = ∠EBC …. (iii)
But ∠EBC + ∠ABC = 180° (a linear pair]
∠D + ∠ABC = 180° (using (iii)]
Now, a pair of opposite angles of quadrilateral ABCD is supplementary
Thus, ABCD is a cyclic quadrilateral i.e., A, B, C and D’are concyclic. In ΔABD and ΔDCA
∠ABD = ∠ACD [∠s in the same segment for cyclic quad. ABCD]
∠BAD = ∠CDA [using (i)]
AD = AD (common]
So, by using AAS congruence axiom, we have
ΔABD ≅ ΔDCA
Hence, BD = CA [c.p.c.t.]
|
40 videos|563 docs|57 tests
|
FAQs on Class 9 Maths Chapter 8 Previous Year Questions - Quadrilaterals
| 1. What are the properties of quadrilaterals? |  |
| 2. How do you calculate the area of different quadrilaterals? |  |
| 3. What is the significance of the diagonals in quadrilaterals? |  |
| 4. How do you prove that a quadrilateral is a parallelogram? |  |
| 5. What are some real-life applications of quadrilaterals? |  |

















