Class 9 Maths Chapter 12 Previous Year Questions - Surface Area & Volumes
Very Short Answer Type Questions
Q1. Total surface area of a cube is 96 cm2. What is its volume?
Sol:
Total surface area of the cube = 6l2
∴ 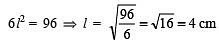
Thus, the volume of the cube = l3 = 43 = 64 cm3
Q2. If the total surface area of a sphere is 154 cm2. Find its total volume.
Sol:
Let ‘r’ be radius of the sphere
∴ Total S.A. = 4 π r2 = 154 cm2
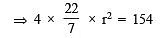
or 
Now,
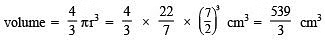
Q3. If the radius of a sphere is 3r then what is its volume?
Sol:
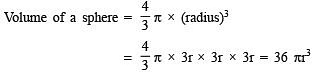
Short Answer Type Questions
Q1. If the circumference of the base of a right circular cylinder is 110 cm, then find its base area.
Sol:
Let r be the radius of the base of the cylinder.
∴ Circumference = 2πr = 2 x(22/7)x r
Now, 2 x(22/7) x r= 110
⇒ 
Now, Base area = 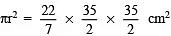
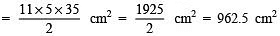
Q2. If the radius of a sphere is doubled, then find the ratio of their volumes.
Sol:
Let the radius of the original sphere = r
∴ Radius of new sphere = 2r
∴ Ratio of their volumes = 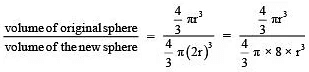
Q3. If the radius of a sphere is such that πr2 = 6cm2 then find its total surface area.
Sol: ∵ πr2 = 6cm2
∴ Curved S.A. of the hemisphere 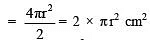 = 2 × 6 cm2 = 12 cm2
= 2 × 6 cm2 = 12 cm2
Also, plane S.A. of the hemisphere = π r2 = 6 cm2
⇒ Total S.A. = C.S.A. + plane S.A. = 12 cm2 + 6 cm2 = 18 cm2
Q4. Find the slant height of a cone whose radius is 7 cm and height is 24 cm.
Sol:
Here, h = 24 cm and r = 7 cm
Since,
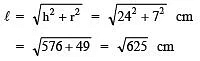

= 25 cm
∴ Slant height = 25 cm.
Q5. The diameter of a road roller, 120 cm long is 84 cm. If it takes 500 complete revolutions to level a playground, find the cost of levelling it at  2 per square metre.
2 per square metre.
Sol:
Here, radius (r) = 42 cm
Length of the roller = Height of the cylinder
⇒ h = 120 cm
∴ Curved surface area of the roller = 2πrh =2 x(22/7) x 42 x 120 cm2
= 2 x 22 x 6 x 120 cm2 = 31680 cm2
∴ Area levelled in one revolution = 31680 cm2
⇒ Area levelled in 500 revolutions = 31680 x 500 cm2

∴ Cost of levelling the playground = 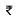 2 x 15840 =
2 x 15840 = 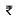 31680.
31680.
Q6. How many lead balls, each of radius 1 cm, can be made from a sphere of radius 8 cm?
Sol:
Radius of the lead ball (r) = 1 cm
∴ Volume of a lead ball = 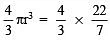 x 1 x 1 x 1 cm3
x 1 x 1 x 1 cm3
= (4/3) x (22/7) cm3
Radius of the sphere (r) = 8 cm
∴ Volume of a sphere = 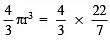 x 8 x 8 x 8 cm3
x 8 x 8 x 8 cm3
Let the required number of balls = n
∴ [Volume of n-lead balls] = [Volume of the sphere]
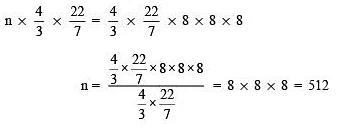
Thus, the required number of balls is 512.
Long Answer Type Questions
Q1: Find the capacity in litres of a conical vessel having height 8 cm and slant height 10 cm.
Sol:
Height of conical vessel (h) = 8 cm
Slant height of conical vessel (l) = 10 cm
∴ r2 + h2 = l2
⇒ r2 + 82 = 102
⇒ r2 = 100 – 64 = 36
⇒ r = 6 cm
Now, volume of conical vessel = 1/3πr2h
= 1/3 × 227 × 6 × 8
= 301.71 cm3
= 0.30171 litre
Q2: A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find it volume. If 1m3 wheat cost is ₹10, then find total cost.
Sol:
Diameter of cone = 10.5 m
Radius of cone (r) = 5.25 m
Height of cone (h) = 3 m
Volume of cone = 13πr2h
= 13 × 22/7 × 5.25 × 5.25 × 3
= 86.625 m3
Cost of 1m3 of wheat = ₹10
Cost of 86.625 m3 of wheat = ₹10 × 86.625
= ₹866.25
Q3: A cylindrical vessel can hold 154 g of water. If the radius of its base is 3.5 cm, and1cm3 of water weighs 1 g, find the depth of water.
Sol:
Since 1 cm3 of water weighs 1 g.
∴ Volume of cylindrical vessel = 154 cm3
πr2h = 154
22/7 × 3.5 × 3.5 × h = 154
h = 4cm
Hence, the depth of water is 4 cm.
Q4: The volume of cylindrical pipe is 748 cm. Its length is 0.14 m and its internal radius is 0.09 m. Find thickness of pipe.
Sol:
Internal radius (r) of cylindrical pipe = 0.09 m = 9 cm
Length (height) of cylindrical pipe (h) = 0.14 m = 14 cm
Let external radius of the cylindrical pipe be R cm.
Volume of cylindrical pipe = 748 cm3
⇒ π(R2 – r2)h = 748
⇒ 22/7 (R2 – 92)14 = 748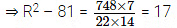
⇒ R2 = 81 + 17 = 98
⇒ R = √98 = 7√2 cm = 9.9 cm
Thus, thickness of the pipe = 9.9 -9 = 0.9 cm
Q5: The curved surface area of a cylinder is 154 cm. The total surface area of the cylinder is three times its curved surface area. Find the volume of the cylinder.
Sol:
Since curved surface area of cylinder = 154 cm2 (given]
Total surface area of cylinder = 3 × curved surface area
2πrh + 2πr2 = 3 × 154 3 154 + 2πr2 = 462
2πr2 = 462 – 154 = 308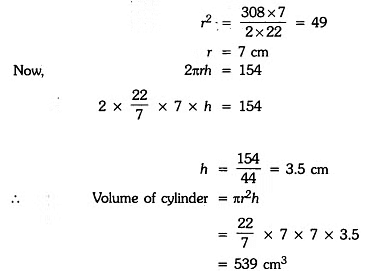
= 539 cm3
Q6: A right triangle of hypotenuse 13 cm and one of its sides 12 cm is made to revolve taking side 12 cm as its axis. Find the volume and curved surface area of the solid so formed.
Sol:
Here, hypotenuse and one side of a right triangle are 13 cm and 12 cm respectively.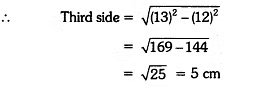
Now, given triangle is revolved, taking 12 cm as its axis
∴ Radius of the cone (r) = 5 cm
Height of the cone (h) = 12 cm
Slant height of the cone (1) = 13 cm
∴ Curved surface area = πrl = π(5)(13) = 65π cm2
Volume of the cone = 1/2πr2h = 1/2π × 5 × 5 × 12 = 100π cm3
Hence, the volume and curved surface area of the solid so formed are 100 π cm3 and 65 π cm2 respectively.
|
44 videos|412 docs|54 tests
|

|
Explore Courses for Class 9 exam
|

|


















