Vectors and their Addition & Subtraction | Physics Class 11 - NEET PDF Download

Introduction

It is obvious in scalar algebra, that 3+4 = 7. But if for instance we assume that 3 and 4 are vectors rather than scalars, then 3+4 could be anything between -7 to +7. Sounds interesting ! 

This is the real power of vectors. Let's learn about vectors! 

Vectors and their Representation

• A quantity is said to be a vector if it satisfies the following conditions:
  (a) It obeys the law of parallelogram addition (discussed later in document).
  (b) It has a specified direction.
• A vector is represented by a line with an arrowhead.
• The point O from which the arrow starts is called the tail or initial point, or origin of the vector.
• Point A, where the arrow ends, is called the tip or head or terminal point of the vector.
• A vector displaced parallel to itself remains unchanged.

Types of Vectors

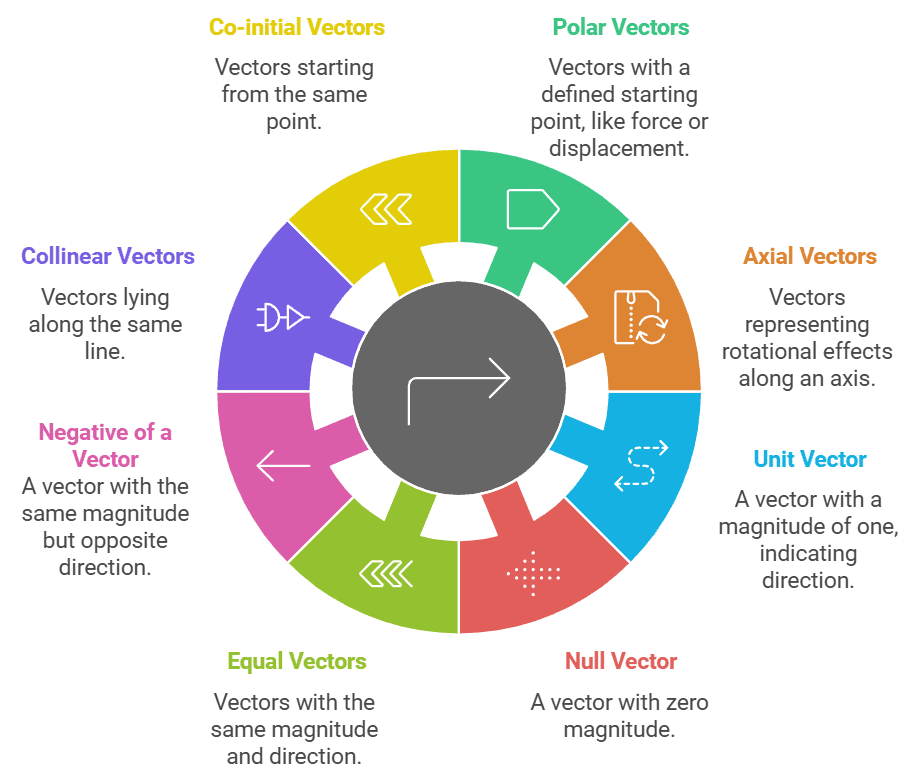Types of Vectors

Laws of Addition and Subtraction of Vectors

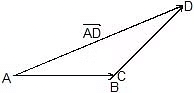
1. Triangle Law of Vector Addition of Two Vectors

When two non-zero vectors are represented by two sides of a triangle taken in the same order, the resultant vector can be determined by the closing side of the triangle in the opposite direction.

Mathematically, this is expressed as: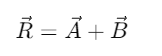

Steps for adding two vectors representing same physical quantity by triangle law:

•  Keep vectors such that tail of one vector coincides with head of others.
•  Join tail of first to head of the other by a line with arrow at head of the second.
• This new vector is the sum of two vectors. (also called resultants)

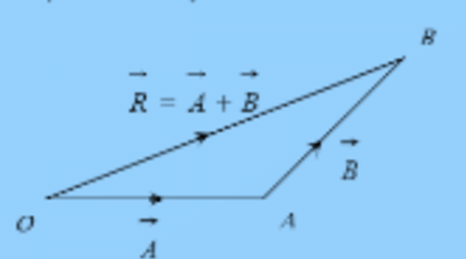
Magnitude of the Resultant Vector

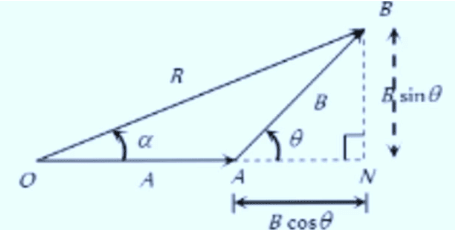
In triangle 
ABN:

The cosine of the angle θ is given by:

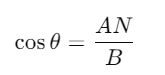
⇒ AN = B Cosθ

The sine of the angle $\mathrm{<span\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">\theta \; is\; represented\; as:</span>}$

$\mathrm{<span\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;"><img\; src="https://cn.edurev.in/cdn\_assets/v323/assets/img/ph.png"\; style="display:\; block;\; margin:\; 5px\; auto;\; text-align:\; center;\; max-width:\; calc(100\%\; -\; 5px);\; cursor:\; pointer;\; padding:\; 0px\; 1px;\; user-select:\; none;\; word-break:\; break-word;\; letter-spacing:\; inherit;"\; fr-original-class="fr-draggable"\; alt="Vectors\; and\; their\; Addition\; \&\; Subtraction\; |\; Physics\; Class\; 11\; -\; NEET"\; data-src="https://edurev.gumlet.io/ApplicationImages/Temp/24733558\_3f751479-ca7d-45aa-9051-68e6d37dba59\_lg.png">\; \Rightarrow \; <strong\; style="font-weight:\; 700;\; word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">BN\; =\; B\; Sin\; \theta </strong><br\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;"></span>}$

$\mathrm{<span\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 22px;\; letter-spacing:\; inherit;\; color:\; black;"><strong\; style="font-weight:\; 700;\; word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 22px;\; letter-spacing:\; inherit;\; color:\; black;">Direction\; of\; resultant\; vectors:</strong> </span>}$

$ If θ is angle between  and  then$

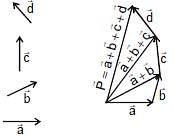
2. Polygon Law of Vector Addition  

When several non-zero vectors are represented by the sides of an $nn$n-sided polygon, the resultant vector can be determined by the closing side of the polygon, which corresponds to the $\mathrm{<span\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">n\; side,\; taken\; in\; the\; opposite\; direction. </span>}$

The resultant is given by: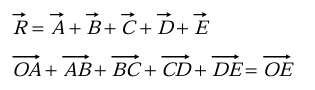

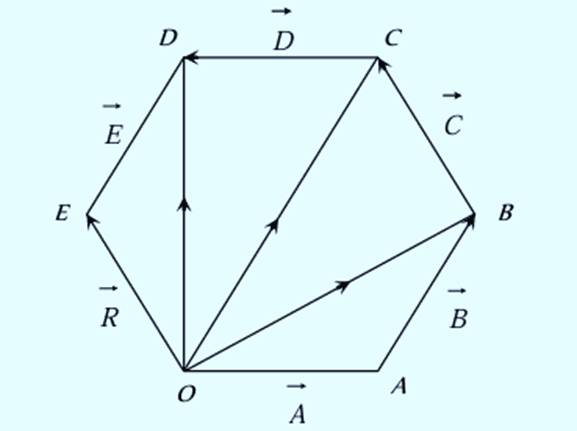
• This law is used for adding more than two vectors. 
• This is extension of triangle law of addition. 
• We keep on arranging vectors such that tail of next vector lies on head of former.
•  When we connect the tail of first vector to head off last, we get resultant of all the vectors.

Note: 

• Resultant of two unequal vectors can not be zero.
• Resultant of three co-planar vectors may or may not be zero.
• Resultant of three non co-planar vectors can not be zero.

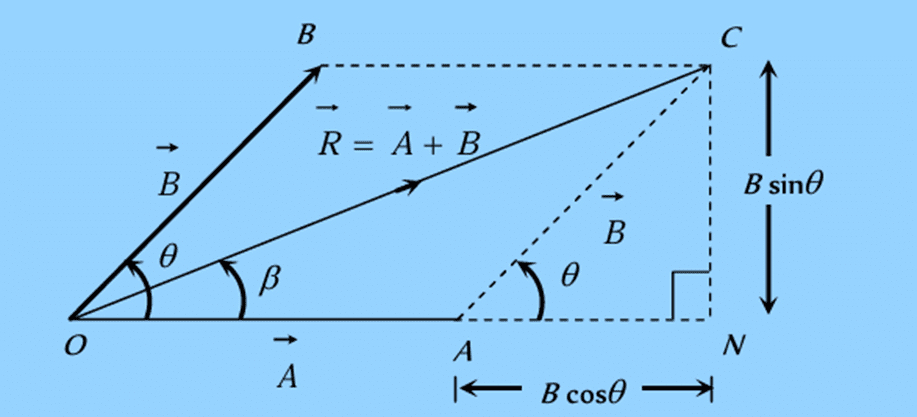
3. Parallelogram Law of Vector Addition 

When two non-zero vectors are depicted as the two adjacent sides of a parallelogram, the resultant vector is represented by the diagonal of the parallelogram that passes through the intersection point of the two vectors.

Steps : 

•  Keep two vectors such that their tails coincide.
•  Draw parallel vectors to both of them considering both of them as sides of a parallelogram.
•  Then the diagonal drawn from the point where tails coincide represents the sum of two vectors, with its tail at point of coincidence of the two vectors.

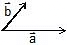
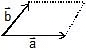
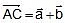
Magnitude of resultant vectors:

In triangle ONC:

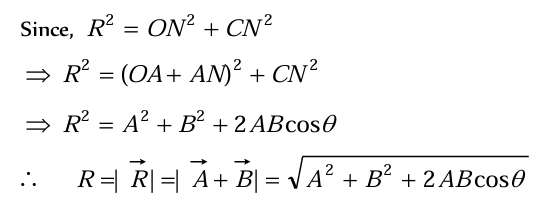
Special cases: 
(i) R = A + B when θ = 0°

(ii) R = A - B when θ = 180°

(iii)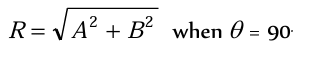

Direction of resultant vectors:

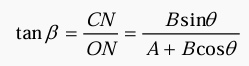
Important points :

•  To a vector, only a vector of same type can be added that represents the same physical quantity and the resultant is also a vector of the same type.
•  As R = [A² + B² + 2AB cosθ]^1/2 so R will be maximum when, cosθ = max = 1,

               i.e., θ = 0º, i.e. vectors are like or parallel and R_max = A + B.

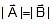•   and angle between them θ then R =
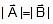•   and angle between them π -θ then R =
•  The resultant will be minimum if, cos θ = min = -1, i.e., θ = 180º, i.e. vectors are antiparallel and R_min = A -B.
•  If the vectors A and B are orthogonal, i.e., θ = 90º,
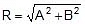
•  As previously mentioned that the resultant of two vectors can have any value from (A -B) to (A + B) depending on the angle between them and the magnitude of resultant decreases as q increases 0º to 180º.
•  Minimum number of unequal coplanar vectors whose sum can be zero is three.
•  The resultant of three non-coplanar vectors can never be zero, or minimum number of non coplanar vectors whose sum can be zero is four.

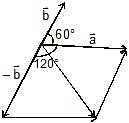
Subtraction of Vectors

Negative of a vector say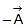 is a vector of the same magnitude as vector but pointing in a direction opposite to that of .

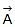Thus, 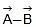 can be written as  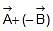or 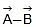 is really the vector addition of  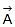and .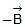

Suppose angle between two vectors and is θ. Then angle between 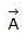and 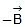 will be 180° -θ as shown in figure.

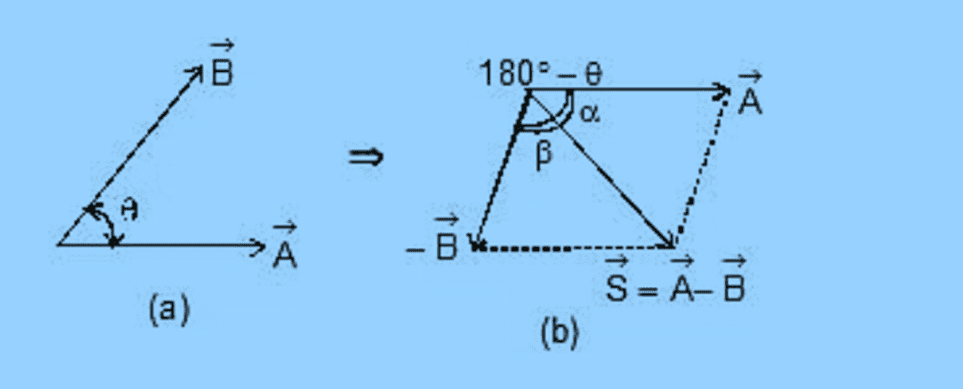
Magnitude of 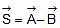 will be thus given by

S =  =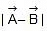

or S = 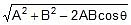 ...(i)

tanα = 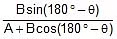 =  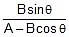...(ii)

or tanβ = 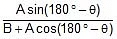 =  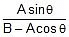...(iii)

Ex 1. Two vectors of 10 units & 5 units make an angle of 120° with each other. Find the magnitude & angle of resultant with vector of 10 unit magnitude. 

Sol: Given,

a = 10 units, b = 5 units and angle = 120º

Magnitude is given by,

=

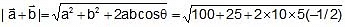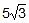
Angle of resultant with vector of 10 unit magnitude will be,

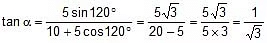
⇒ α = 30°

[Here shows what is angle between both vectors = 120° and not 60°]

Note: can also be found by making triangles as shown in the figure. (a) and (b)

                  Or                        

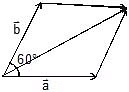
Ex 2. Two vectors of equal magnitude 2 are at an angle of 60° to each other find magnitude of their sum & difference. 

Sol. Given, 

a = b = 2 units and angle = 60º

Magnitude is given by,

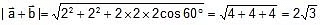
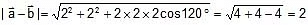
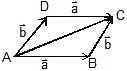
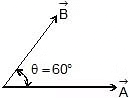
Ex 3.     Find  and 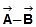 in the diagram shown in figure. Given A = 4 units and B = 3 units.

Sol. Addition : 

R =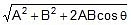

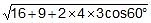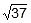=  =  units

tanα = 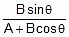 =  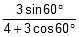= 0.472

a = tan^-1(0.472) = 25.3°

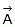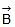Thus, resultant of  and  is 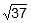 units at angle 25.3° from  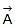in the direction shown in figure.

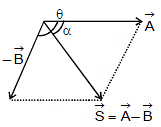
Subtraction : 

S =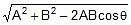

=  =

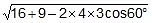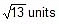
and tanθ =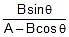

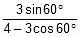=  = 1.04

∴ α = tan^-1 (1.04) = 46.1°

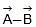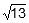Thus,  is  units at 46.1° from  in the direction shown in figure.

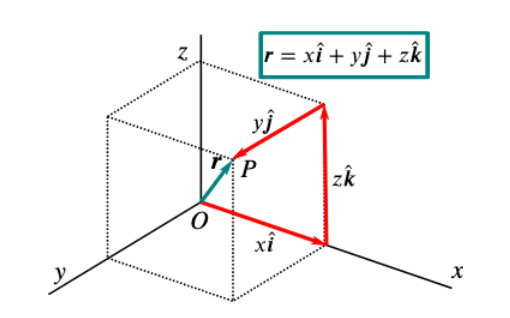
Position Vector 

Position vector is a vector that gives the position of a point with respect to the origin of the coordinate system. 

The magnitude of the position vector is the distance of the point P from the origin O. Vector OP is the position vector that gives the position of the particle with reference to O.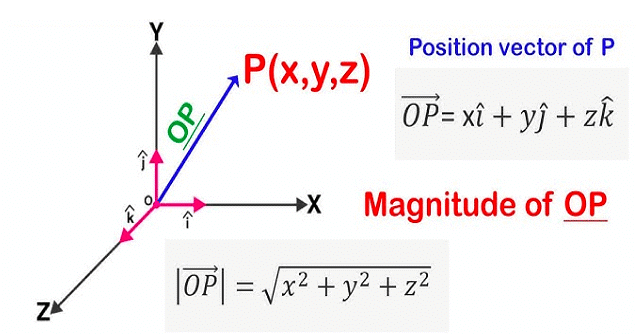

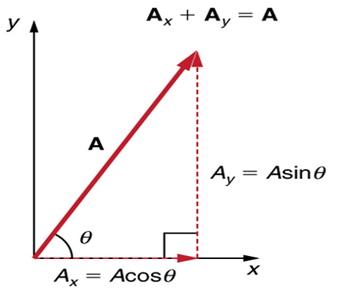
Resolution of Vectors Into Component

If   the resultant, then conversely  i.e. the vector  can be split up so that the vector sum of the split parts equals the original vector   If the split parts are mutually perpendicular then they are known as components of  and this process is known as resolution.

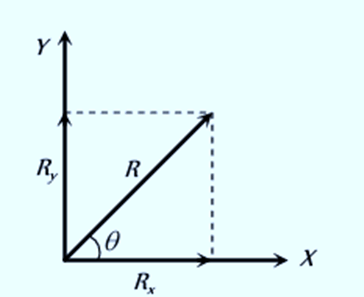
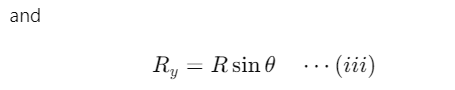
Since R and θ are usually known, Equation (ii) and (iii) give the magnitude of the components of   along x and y axes respectively.

A vector is resolved into its components, the components themselves can be used to specify the vector as:

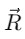
1. The magnitude of the vector $<span\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;"> is\; obtained\; by\; squaring\; and\; adding\; equation\; (ii)\; and\; (iii),\; i.e.</span>$

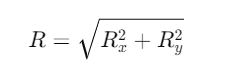
2. The direction of the vector 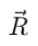 is obtained by dividing equation (iii) by (ii), i.e.

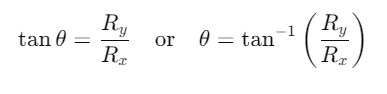
Products of Vectors

• There are two kinds of multiplication for vectors. One kind of multiplication is the scalar product, also known as the dot product.
• The other kind of multiplication is the vector product, also known as the cross product.
• The scalar product of vectors is a number (scalar).
• The vector product of vectors is a vector.
• The scalar product is discussed in detail in the document: Scalar Product of Vector.
•  The vector product is discussed in detail in the document: Cross Product of Vector.