Important Formulas: Time, Speed and Distance | Quantitative for GMAT PDF Download
| Table of contents |

|
| Speed, Time and Distance |

|
| Relationship Between Speed, Time and Distance |

|
| Conversion of Speed, Time and Distance |

|
| Examples |

|
In GMAT-level questions, understanding speed, time, and distance is essential, as these problems test both mathematical reasoning and the ability to manage multiple conditions in word problems.

The key formula connecting these three variables is: Distance = Speed x Time.
Speed, Time and Distance
The speed of a body is the distance covered by the body per unit time i.e. Speed = Distance/Time.
- Speed: Speed is the rate at which a particular distance is covered by an object in motion.
- Time: Time is an interval separating two events.
- Distance: Distance is the extent of space between two points.
Units of Speed Time and Distance
Each of the speed, distance and time can be represented in different units:
- Time can be generally expressed in terms of seconds(s), minutes (min) and hours (hr).
- Whereas the distance is generally expressed in meters (m), kilometres (km), centimetres, miles, feet, etc.
- Speed is commonly expressed in m/s, km/hr.
- For Example, If the distance is given in km and time in hr. then as per the formula:
Speed = Distance/ Time ; the unit of speed will become km/ hr.
Relationship Between Speed, Time and Distance
Now that we are well aware of the definition of speed, distance and time let us understand the relationship between them.
It is said that an object attains motion or movement when it changes its position with respect to any external stationary point. Speed, Time and Distance are the three variables that represent the mathematical model of motion as, s x t = d.
- Time is directly proportional to distance. It means that speed remains constant, if we have two vehicles moving two distances for two different time duration then the time is directly proportional to the distance.
- Speed is directly proportional to distance. It means that time remains constant if we have two vehicles moving two distances at two different speeds respectively.
- Speed is Inversely Proportional to time. It means that distance remains constant if we have two vehicles moving at two different speeds and taking times respectively.
The formula for speed calculation is Speed = Distance/Time
This shows us how slow or fast a target moves. It represents the distance covered divided by the time needed to cover the distance.
Speed is directly proportional to the given distance and inversely proportional to the proposed time. Hence,
Distance = Speed x Time and
Time = Distance / Speed since as the speed grows the time needed will decrease and vice versa.
Conversion of Speed, Time and Distance
The conversion of speed, time and distance into various units is given below:
- To convert a given data from km/hour to m/sec, we multiply by 5/18. As
1 km/hour = 5/18 m/sec. - To convert a given data m/sec to km/hour, we multiply by 18/5. As
1 m/sec = 18/5 km/hour = 3.6 km/hour.
In terms of formula, we can list it as: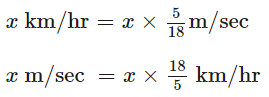
Similarly, some other conversions are given below:
- 1 km/hr = 5/8 miles/hour
- 1 yard = 3 feet
- 1 kilometer= 1000 meters
- 1 mile= 1.609 kilometer
- 1 hour= 60 minutes= 3600 seconds
- 1 mile = 1760 yards
- 1 yard = 3 feet
- 1 mile = 5280 feet
Applications of Speed, Time and Distance
Some of the major applications of speed, time and distance are given below:
Average Speed
- The average speed is determined by the formula = (Total distance travelled)/(Total time taken)
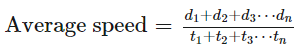
- When the distance travelled is constant and two speed is given then the formula for average speed is:

where x and y are the two speeds at which the corresponding distance has been reached. - When the time taken is constant average speed is calculated by the formula:

where x and y are the two speeds at which we covered the distance for an identical time. - If the first part of any given distance is covered at a rate of v1 in time t1 and the second part of the distance is covered at a rate v2 in time t2 then the average speed is given by the formula:
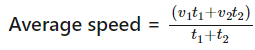
Example: An individual drives from one place to another at 40 km/hr and returns at 160 km/hr. If the complete time needed is 5 hours, then obtain the distance.
Sol: Here the distance is fixed, so the time taken will be inversely proportional to the speed. The ratio of speed is given as 40:160, i.e. 1:4.
Therefore the ratio of time taken will be 4:1.
Total time is practised = 5 hours; therefore the time taken while travelling is 4 hours and returning is 1 hour.
Hence, distance = 40x 4 = 160 km.
Relative Speed
- As the name suggests the idea is about the relative speed between two or more things.
- The basic concept of relative speed is that the speed gets combined in the case of objects moving in the opposite direction to one another and the speed gets subtracted for the case when objects are moving in an identical direction.
- If two passenger trains are travelling in opposite directions with a speed of X km/hr and Y km/hr respectively. Then their relative speed is given by the formula:
Relative speed = X + Y
In this case, the time taken by the train in passing each other is given by the formula:
Relative speed = X + Y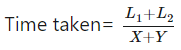
Here L1, L2 are the lengths of the trains respectively. - On the other hand, if the two trains are travelling in the same direction with the speed of X km /hr and Y km/hr respectively. Then their relative speed is given by the formula:
Relative speed = X -Y
Inverse Proportionality of Speed & Time
- Speed is said to be inversely proportional to time when the distance is fixed.
- In mathematical format, S is inversely proportional to 1/T when D is constant.
- For such a case if the speeds are in the ratio m:n
then the time taken will be in the ratio n:m. - There are two approaches to solving questions:
Applying Inverse Proportionality
Applying Constant Product Rule
Examples
Example 1: After moving 100km, a train meets with an accident and travels at (3/4)th of the normal speed and reaches 55 min late. Had the accident occurred 20 km further on it would have arrived 45 min delayed. Obtain the usual Speed?
Sol: Applying Inverse Proportionality Method
Here there are 2 cases
Case 1: accident happens at 100 km
Case 2: accident happens at 120 km
The difference between the two incidents is only for the 20 km between 100 km and 120 km. The time difference of 10 minutes is just due to these 20 km.
In case 1, 20 km between 100 km and 120 km is covered at (3/4)th speed.
In case 2, 20 km between 100 km and 120 km is reached at the usual speed.
So the usual time “t” taken to cover 20 km, can be found as follows. 4/3 t – t = 10 mins = > t = 30 mins, d = 20 km
so the usual speed = 20/30min = 20/0.5 = 40 km/hr.Using Constant Product Rule Method: Let the actual time taken be equal to T.
There is a (1/4)th reduction in speed, this will result in a (1/3)rd increase in time taken as speed and time are inversely proportional to one another.
A 1/x increment in one of the parameters will result in a 1/(x+1) reduction in the other parameter if the parameters are inversely proportional.
The delay due to this reduction is 10 minutes
Thus 1/3 T= 10 and T=30 minutes or 0.5 hour
Also, Distance = 20 km
Thus Speed = 40 kmph
Meeting Point Question
If two individuals travel from two locations P and Q towards each other, and they meet at point X. Then the total distance traversed by them at the meeting will be PQ. The time taken by both of them to meet will be identical.
As the time is constant, the distances PX and QX will be in the ratio of their speed. Assume that the distance between P and Q is d.
If two individuals are stepping towards each other from P and Q respectively, when they meet for the first time, they collectively cover a distance “d”. When they meet each other for the second time, they mutually cover a distance “3d”. Similarly, when they meet for the third time, they unitedly cover a distance of “5d” and the process goes on.
Take an example to understand the concept:
Example 2: Ankit and Arnav have to travel from Delhi to Hyderabad in their respective vehicles. Ankit is driving at 80 kmph while Arnav is operating at 120 kmph. Obtain the time taken by Arnav to reach Hyderabad if Ankit takes 9 hrs.
Sol: As we can recognise that the distance covered is fixed in both cases, the time taken will be inversely proportional to the speed. In the given question, the speed of Ankit and Arnav is in a ratio of 80: 120 or 2:3.
Therefore the ratio of the time taken by Ankit to that taken by Arnav will be in the ratio 3:2.
Hence if Ankit takes 9 hrs, Arnav will take 6 hrs.
Example 3: A car travels 120 km at a speed of 40 km/h and then travels another 180 km at a speed of 60 km/h. What is the average speed for the entire journey?
Sol:
Calculate time for each segment:
- Time for 120 km at 40 km/h: 3 hours
- Time for 180 km at 60 km/h: =3 hours
Total distance and total time:
- Total distance = 120 km + 180 km = 300 km
- Total time = 3 hours + 3 hours = 6 hours
Average speed:
Example 4: A person drives from City X to City Y at 60 km/h and returns at 40 km/h. What is the average speed for the entire trip?
Sol:
Let the distance between City X and City Y be km.
Time taken for each leg:
- Time from X to Y:
- Time from Y to X:
Total distance and total time:
- Total distance =
- Total time =
Average speed:
(2d/5d)x 120 = 48km/h
Alternatively,
We can also use the formula = 2xy/(x+y)
where, x = 60km/h and y = 40km/h
After putting the values we get average speed = 4800/100 = 48km/hr
|
121 videos|148 docs|111 tests
|
FAQs on Important Formulas: Time, Speed and Distance - Quantitative for GMAT
| 1. What is the formula to calculate speed, and how is it derived? |  |
| 2. How can I convert speed from kilometers per hour (km/h) to meters per second (m/s)? |  |
| 3. What is the relationship between time, speed, and distance in practical scenarios? |  |
| 4. How can I solve problems involving time, speed, and distance using examples? |  |
| 5. What are common units used for measuring speed, time, and distance? |  |




















