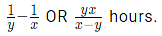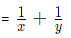Important Formulas: Pipe & Cisterns | Quantitative for GMAT PDF Download
Definition of Pipes & Cisterns
- A pipe is connected to a tank or cistern to fill or empty the tank or cistern
- Inlet: A pipe which is connected to fill a tank is known as an inlet.
- Outlet: A pipe which is connected to empty a tank is known as an outlet.
- In pipes and cisterns problems – we need to find out what portion of the tank each of the pipes fill or drain in unit time (say in a minute or hour or second) and then perform arithmetic operation on this value.
Formulas for Pipes and Cisterns
- If pipe can fill a tank in x hours , then part filled in one hour = 1/x
- If pipe can empty a tank in y hours , then part emptied in one hour = 1/y
- If pipe A can fill a tank in x hours, Pipe B can empty the full tank in y hours (where y > x). Then, on opening both the pipes, the net part filled in one hour=

- If pipe A can empty a tank in X hours. Pipe B can empty the same tank in Y hours. Then part of the tank emptied in one hour when both the pipes start working together

Example 1: Tarun and Varun started a game in which they checked whose pipe fills the tank faster Tarun’s pipe A and Varun’ s pipe B can fill a cistern in 6 hours and 8 hours, respectively. If both pipes are opened simultaneously, how long will they take to fill the cistern?
Sol:
Let the total capacity of the cistern be C (considering 1 unit of capacity).
The filling rate of Pipe A = 1/6 (fraction of the cistern filled per hour). The filling rate of Pipe B = 1/8 (fraction of the cistern filled per hour).
When both pipes are opened simultaneously, their filling rates are additive:
Combined filling rate = (1/6) + (1/8) = 7/24 (fraction of the cistern filled per hour).
Now, to find the time it will take to fill the cistern, we use the formula:
Time = 1 / Combined filling rate
Time = 1 / (7/24) = 24 / 7 ≈ 3.43 hours
Hence They will take approximately 3 hours and 26 minutes to fill the cistern when both pipes A and B are opened simultaneously.
Example 2: A tank has been connected to three pipes such that Pipe A can fill it in 4 hours, Pipe B in 6 hours, and Pipe C can empty it in 8 hours. If all pipes are opened at the same time, how long will it take to fill the tank wholly ?
Sol:
Let the total capacity of the cistern be C (considering 1 unit of capacity).
The filling rate of Pipe A = 1/4 (fraction of the tank filled per hour).
The filling rate of Pipe B = 1/6 (fraction of the tank filled per hour).
The emptying rate of Pipe C = -1/8
All three pipes are opened simultaneously, their net filling rate is the sum of the filling rates of Pipes A and B and the emptying rate of Pipe C:
Net filling rate = (1/4) + (1/6) + (-1/8) = 12/48 + 8/48 – 6/48 = 14/48 (fraction of the tank filled per hour).
Now, to find the time it will take to fill the tank, we use the formula:
Time = 1 / Net filling rate
Time = 1 / (14/48) = 48 / 14 ≈ 3.43 hours
Hence, It will take approximately 3 hours and 26 minutes to fill the tank completely when all three pipes A, B, and C are opened simultaneously
|
115 videos|106 docs|113 tests
|

|
Explore Courses for GMAT exam
|

|