Class 10 Maths Chapter 11 Important Question Answers - Areas Related to Circles
| Table of contents |

|
| Very Short Answer Type Questions- I |

|
| Very Short Answer Type Questions- II |

|
| Short Answer Type Questions |

|
| Long Answer Type Questions |

|
Very Short Answer Type Questions- I
Unless stated otherwise, take π = 22/7.
Q1: The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Ans: Let us suppose R, radius of the circle whose circumference is equal to the circumference of the two circles with radius 19 cm and 9 cm respectively.

Very Short Answer Type Questions- II
Q2: The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Ans: Area of a circle is given by, πR2.
Let R be the radius of the circle whose area is equal to the sum of the areas of the two circles of radii 8 cm and 6 cm, respectively.
Thus, we have:


Q3: Figure depicts an archery target marked with its five scoring area from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of the five scoring regions.

Ans: Given, diameter of the region representing Gold score as 21cm and the width of other bands as 10.5 cm.
Thus, radius of the Gold scoring region, R = 21/2 cm.
Area of a circle is given by, πR2.
Area of the Gold scoring region, 
⇒ A gold = 346.5 cm2
Area of scoring region = Area of previous circle – Area of next circle.
∴ Area of Red scoring region, 
⇒ Ared=1386−346.5
⇒ Ared=1039.5 cm2
Area of Blue scoring region, 
⇒ Ablue = 3118.5−1386
⇒ Ablue = 1732.5 cm2
Area of Black scoring region,
⇒ Ablack = 5544−3118.5
⇒ Ablack = 2425.5 cm2
Area of White scoring region,
⇒Awhite=8662.5−5544
⇒Awhite=3118.5 cm2
Q4: The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
Ans: Given, diameter of car wheel =80 cm.
∴ Radius of the car wheel =40 cm.
Distance covered by the wheel in one revolution is equal to the circumference of the wheel.
∴2πR = 2 × (22/7) x 40
Thus, distance covered by the wheel in one revolution is equal to 1760/7 cm.
Given, the distance covered in 1 hour =66km=6600000cm
Hence, distance covered by the wheel in 10 minutes = 
Number of revolutions = 
Number of revolutions = 
Hence, number of revolutions =4375.
Q5: Find the area of a sector of a circle with radius 6 cm, if angle of the sector is 60°.
Ans: Given, Angle of the sector is 60°.
Radius, r = 6 cm
Area of the sector of a circle = 

Q6: Find the area of a quadrant of a circle whose circumference is 22 cm.
Ans: Given, the circumference of the circle as 22 cm.
We know, the circumference of a circle is given by, 2πR.
Therefore, 2πR = 22
⇒ R = 3.5 cm
For the quadrant of a circle, θ = 90°
Area of quadrant is given by, 

∴ Area of the quadrant of the circle = 9.625 cm2.
Q7: The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Ans: Given, length of the minute hand (radius) , r = 14 cm and from the given data we interpret the angle in the clock, θ = 30°.
Area swept by the minutes hand in 5 minutes,

Q8: A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding: (Use π=3.14)
(i) minor segment
Ans: Given, Radius, r =10 cm and the angle, θ = 90°.
Area of minor sector, 

Area of ΔOAB, = (1/2) Base × Height.
Area of minor segment can be obtained as,
Area of minor segment = Area of minor sector − Area of △OAB.
⇒ A = 78.550
⇒ A = 28.5 cm2
(ii) Major Segment
Ans: For major sector, radius = 10 cm and θ = 360°−90° = 270°
∴ Area of major sector 

Q9: A horse is tied to a peg at one corner of a square shape grass field of side 15m by means of a 5 m long rope (see figure).

Find:
(i) the area of that part of the field in which the horse can graze.
Ans: Area of a sector of a circle is given by, 
Area of the part of the field where the horse can graze is in the form of a quadrant with radius, r = 5m.
For the quadrant of a circle, θ = 90°
Thus, the area is given as, 
⇒ A = 19.625 m2 .
(ii) the increase in the grazing area if the rope were 10 m long instead of 5 m.
Ans: Area of quadrant with 10m rope, the radius would be, r = 10m.
Thus, the grazing area for 10 m long rope is given by, 
⇒ A =78.5 m2.
∴ The increase in grazing area can be calculated by subtracting area of 5m rope from the area of 10m rope.
Hence, Increase in area = 78.519.625 = 58.875 m2
Q10: A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find:
(i) The total length of the silver wire required.
Ans: Given, diameter of silver wire circle as 35 mm
Thus, radius is 35/2mm.
Circumference of a circle is given by, 2πr.
Therefore, the circumference of the circle made by silver wire is,
As the wire is used in making 5 diameters,
∴ length of 5 diameters, L=35×5
⇒ L = 175 mm ……(2)
Total length of the silver wire required would be the sum of circumference of the circle and the length of 5 diameters.
Hence, adding equation (1) and (2), we get
⇒ 110 + 175 = 285 mm
(ii) The area of each sector of the brooch.
Ans: Given, diameter of silver wire circle as 35 mm
Thus, radius is 35/2 mm.
Angle of each sector, 
∴ The area of each sector of the brooch is given by, 

Q11: An umbrella has 8 ribs which are equally spaced (see figure). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

Ans: Let umbrella be a flat circle with radius, r = 45 cm.
Given, the umbrella has 8 ribs, thus the angle θ would be, 
Area between two consecutive ribs of the umbrella can be obtained using the formula, 

Q12: A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping an angle of 115°. Find the total area cleaned at each sweep of the blades.
Ans: Given, a car has two wipers with a blade length of 25 cm sweeping an angle of 115°.
Let us suppose radius, r = 25 cm and Angle, θ = 115°.
The two wipers do not overlap.

∴ The total area cleaned at each sweep of the blade will be, 

Hence, area cleaned at each sweep is 1254.96 cm2.
Q13: To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Useπ = 3.14)
Ans: Given, a lighthouse spreads a red light over a sector of angle 80° to a distance of 16.5 km.
Let us suppose radius, r =16.5 km and Angle, θ = 80°.
∴ The area of sea over which the ships are warned is, 

Q14: Find the area of the shaded region in figure, if radii of the two concentric circles with centre O are 7 cm and 14cm respectively and ∠AOC = 40°.

Ans: Area of shaded region ABDC can be determined by subtracting area of sector OBD from the area of sector OAC
, i.e., Area of shaded region ABDC = Area of sector OAC− Area of sector OBD
Area of sector is given by, 
Thus, Area of sector 
Area of sector 
∴ Area of shaded region 

Hence, area of the shaded region is 51.33 cm2.
Q15: Find the area of the shaded region in figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Ans: From the given figure,
Area of shaded region = Area of square ABCD – (Area of semicircle APD + Area of semicircle BPC)
⇒ Area of the shaded region = 
⇒ Area of the shaded region 
∴ Area of the shaded region is 42cm2.
Q16: Find the area of the shaded region in figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
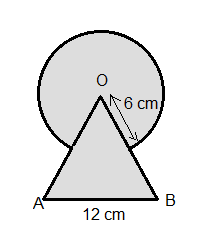
Ans: Area of the shaded region = Area of circle + Area of equilateral triangle OAB - Area of the region common to the circle and the triangle.
Area of a circle is given by, πR2.
Area of equilateral triangle is given by,  (a is the side)
(a is the side)
⇒ Area of the shaded region 
⇒ Area of the shaded region 
Hence, the area of the shaded region is 156.63 cm2.
Q17: From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter of 2 cm is cut as shown in figure. Find the area of the remaining portion of the figure:

Ans: Given, a square of side 4 cm. Four quadrants of a circle of radius 1 cm are cut from each corners of the square.
Also, a circle of diameter 2 cm is cut.
∴ Area of the remaining portion = Area of square – (4× Area of quadrant of radius 1 cm + Area of circle of diameter 2 cm).
Area of a square is given as (side)2.
Area of a circle is given by, πR2.
Similarly, area of quadrant is given by 
Thus,
Area of the remaining portion 
⇒ Area of the remaining portion = 
Hence, area of the remaining portion is 9.71 cm2.
Q18: In a circular table cover of radius 32cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in figure. Find the area of the design (shaded region).

Ans: Given, circular table cover of radius, r = 32cm and an equilateral triangle ABC is drawn in the middle.

Area of the design can be obtained by,Area of design = Area of circle – Area of the equilateral triangle ABC.
Area of a circle is given by, πR2.
Area of equilateral triangle is given by,  (a is the side).
(a is the side).
Thus, area of design = 
∵ G is the centroid of the equilateral triangle.
∴ radius of the circumscribed circle = (2/3)h cm
So, we have 32 = 2/3h
⇒ h = 48 cm
From the figure of equilateral triangle, 

Substituting for a in equation (1), we get:
Thus, area of the design is 1888.08 cm2.
Q19: In figure ABCD is a square of side 14cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region.

Ans: Given, a square of side 14 cm. With the corners of the square as centres four circles are drawn.
Thus, area of the shaded region = Area of the square – (4× Area of sector)
Area of a circle is given by, πR2 and area of sector is given by,  Area of the shaded region =
Area of the shaded region = 
Hence,areaoftheshadedregionis 42\text{ }c{{m}^{2}}$.
Q20: The given figure depicts a racing track whose left and right ends are semi-circular. The difference between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10m wide,

find:
(i) The distance around the track along its inner edge,
Ans: Given that, difference between the two inner parallel line segments is 60m and they are each 106m long and the track is 10m wide.
Distance around the track along its inner edge


(ii) The area of the track.
Ans: Area of track can be calculated as,
Q21: In figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

Ans: Given, radius of the bigger circle, OA or R = 7 cm.
Diameter of the smaller circle is the radius of the bigger circle.
Thus, Radius of the smaller circle, r= 7/2 cm.
Area of the circle is given by, πR2 and
Area of the semicircle is given by, πR2/2.
ΔACB is made up of two right- angled triangles and we know, area of a right-angled triangle is given as 1/2 x base × height .
Area of the shaded region can be obtained as:
Area of shaded region = Area of smaller circle + Area of semicircle ACB − Area of ΔACB.
Area of shaded region = 
Thus, area of the shaded region is 66.5 cm2.
Q22: The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see figure). Find the area of the shaded region. (Use π = 3.14 and √3 = 1.73205)

Ans: Given, area of the equilateral triangle ABC = 17320.5 cm2.
Also, radius of each circle is half the length of the side of the equilateral triangle.
Area of the equilateral triangle is given by, 
Let side of the equilateral triangle ABC be a.
∴ radius of circle, r = 100 cm
Area of the shaded region can be obtained as:
Area of shaded region = Area of the equilateral triangle ABC − 3× Area of the sector.
We know, area of the sector of a circle = 
Thus,
Area of shaded region = 
⇒ 17320.5−15700 = 1620.5cm2
Hence, area of the shaded region is 1620.5 cm2.
Q23: On a square handkerchief, nine circular designs each of radius 7cm are made (see figure). Find the area of the remaining portion of the handkerchief.

Ans: Given, radius of circular design is 7 cm.
Observing the figure, the side of the square is 6×7 = 42 cm.
The handkerchief consists of 9 circular designs.
Thus, area of the shaded region = Area of square ABCD − 9 × Area of circular design.
Area of shaded region = (42×42)−9×π×(7)2
⇒ 1764−1386 = 378 cm2
Hence, area of the shaded region is 378 cm2.
Q24: In figure, OACB is a quadrant of a circle with centre O and radius 3.5cm.

If OD = 2 cm, find the area of the:
(i) quadrant OACB
Ans: Given radius, r = 3.5 cm and OD = 2 cm.
Area of the quadrant of a circle = 
∴ Area of the quadrant 

Area of the quadrant OACB is 9.625 cm2.
(ii) shaded region
Ans: Given radius, r = 3.5 cm and OD = 2 cm.
Area of the shaded region = Area of the quadrant OACB − Area of the triangle BOD.
Area of the shaded region = 
Hence, area of the shaded region is 6.125 cm2.
Q25: In figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π=3.14)

Ans: Given, a square OABC inscribed in a quadrant OPBQ and OA = 20 cm.
∴ OA = AB = BC = OC.
Taking the ΔOAB into consideration and applying Pythagoras Theorem,
OB2= OA2+AB2
⇒ OB2= (20)2+(20)2
⇒ OB = √800
⇒ OB = 20√2 cm
Area of the shaded region = Area of quadrant OPBQ - Area of square OABC
We know, area of the quadrant of a circle = 
∴ Area of shaded region =

Hence, area of the shaded region is 228 cm2.
Q26: AB and CD respectively are the arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see figure). If ∠AOB = 30°. Find the area of the shaded region.

Ans: Given, two arcs AB and CD of two concentric circles with radii 21 cm and 7cm respectively.
Also, ∠AOB = 30°
We know, area of the quadrant of a circle =
Area of the shaded region = Area of arc AB - Area of arc CD.
Hence, area of the shaded region is 102.67 cm2.
Q27: In figure, ABC is a quadrant of a circle of radius 14cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

Ans: Given, a quadrant ABC of a circle of radius 14 cm.
Let us take, ΔABC and apply Pythagoras Theorem.
∴ Radius of the semicircle = 
We know, area of the quadrant of a circle = 
Area of the shaded region BPCQ= Area of BCQB- (Area of BACP - Area of ΔABC).
∴ Area of shaded region = 

Hence, area of the shaded region is 98 cm2.
Q28: Calculate the area of the designed region in figure common between the two quadrants of circles of radius 8 cm each.

Ans: Given, two quadrants each of radii 8 cm which has a design in the common region.
Let us consider the figure as:
Applying Pythagoras Theorem in the right- angled triangle ABC, AC2=AB2+BC2 
From the figure the right triangle AMB,
We know, area of the quadrant of a circle = 
Area of half shaded region = Area of quadrant ABC - Area of ΔABC.
∴ Area of half shaded region = 

Thus, area of designed region can be obtained as, twice the area of half shaded region.
Hence, area of the designed region is 36.57 cm2.
Q29: Find the circumference of a circle of diameter 14cm.
Ans: Given, diameter of circle, d = 14 cm
Circumference of a circle is given by, 2πr
Since, d = 14 cm
Thus, the circumference of the circle is, C=2πr
The circumference of the circle is 44 cm.
Q30: The diameter of a circular pond is 17.5m. It is surrounded by a path of width 3.5m. Find the area of the path.
Ans: Given, diameter of circular pond, d = 17.5 m.
∴ Radius, r =17.5/2 = 8.25 m
It is surrounded by a path of width 3.5m.
∴Outer radius R is the sum of circular pond radius with the width of the surrounded path.
⇒ R = 8.75+3.5 = 12.25 m
Equation for area of path A is given by π[R2−r2].
Hence, area of the path is 231 m2.
Q31: Find the area of the shaded region where ABCD is a square of side 14 cm.

Ans: Given, side of square, a=14 cm.
Area of the shaded region can be calculated by subtracting area of 4 circles from the area of square ABCD, i.e.,
Area of shaded region = Area of square ABCD − 4×Area of circle.
Area of the given square ABCD is given by, A = 14cm×14cm
⇒ A = 196cm2
From the figure, we observe that the diameter of each circle is half the side of the square.
Thus, diameter of circle = 14/2 = 7 cm
∴ Radius of each circle = 7/2cm
Area of the circle =πr2
Hence, area of the shaded region is 42 cm2.
Q32: The radius of a circle is 20cm. Three more concentric circles are drawn inside it in such a manner that it is divided into four parts of equal area. Find the radius of the largest of the three concentric circles.
Ans: Given radius of the circle, r = 20 cm
Area of a circle is given by, A = πr2
Substituting for radius, r.
∴ A = π(20)2
⇒ A = 400πcm2
As the circle is divided into four parts of equal area, area of each circle would be,
⇒ (1/4)400πcm2 = 100πcm2
Let R be the radius of the largest of the three circles and its area is 400π−100π = 300πcm.
Thus the radius, R can be calculated as
Radius of the largest of the three concentric circles is 10√3 cm.
Q33: OACB is a quadrant of a circle with centre O and radius 7cm. If OD = 4cm, then find area of shaded region.

Ans: Given radius r=7 cm and OD=4 cm
Area of quadrant is given by, 
From the figure it is clear that, angle θ = 90°
Area of shaded region = Area of quadrant OACB− Area of ΔAOB
Thus, area of the shaded region is 24.5 cm2.
Q34: A pendulum swings through on angle of 30° and describes an arc 8.8 cm in length. Find the length of pendulum.
Ans: Given, pendulum swings at angle 30°, with an arc of length 8.8 cm.
Sketching the figure, we have:
In the below given figure let r be the length of pendulum and $\angle
AOB={{30}^{{}^\circ }}then,\angle AOB=\dfrac{\pi }{{{180}^{{}^\circ }}}\times {{30}^{{}^\circ }}$
Use θ= l/r to determine the length of the pendulum.
The length of the pendulum is 16.8 cm.
Q35: The cost of fencing a circular field at the rate of Rs. 24 per metre is Rs. 5280. The field is to be ploughed at the rate of Rs.0.50per m2. Find the cost of ploughing the field. (Take π= 22/7)
Ans: As per the question the cost of fencing a circular field at the rate of Rs24, per meter is Rs 5280.
With Rs. 24, the length of fencing =1 metre
∴ for Rs.5280, the length fencing = (1/24)×5280=220meters
∴ Perimeter i.e., circumference of the field =220meters
Let r be the radius of the field.
Circumference is given by, 2πR
Hence, the cost of ploughing the field is Rs.1925.
Q36: Find the difference between the area of regular hexagonal plot each of whose side 72 m and the area of the circular swimming take in scribed in it. (Take π=22/7)
Ans: Given, side of hexagonal plot =72m
Area of equilateral triangle is given by 

Q37: In the given figure areas have been drawn of radius 21cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.

Ans: Given, areas drawn with radius 21 cm at vertices, A,B,C and D.
Thus, required area is the area of the circle with radius 21 cm.
Q38: A wheel has diameter 84cm, find how many complete revolutions it must make to complete 792 meters.
Ans: Given, diameter of wheel, d=2r = 84cm.
Distance covered in one revolution = circumference
Circumference of the circle is given by 2πr.
Distance covered in one revolution 
⇒ 22×12 = 264 cm
Thus, for distance covered 264 cm, number of revolutions = 1
∴ For distance covered 792m/ 79200 cm, number of revolutions= 
Number of revolutions to complete 792 m is 300.
Q39: The given figure is a sector of a circle of radius 10.5cm. Find the perimeter of the sector. (Take π= 22/7)

Ans: Given radius, r = 10.5 cm
We know that circumference, i.e., perimeter of a sector of angle P° of a circle with radius R is given by,
∴ Required perimeter can be calculated as,
Thus, the perimeter of a sector is 32 cm.
Q40: A car had two wipers which do not overlap. Each wiper has a blade of length 25cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.
Ans: Given, radius of each wiper = 25cm and sweeping angle, θ=115°.
Since, area of sector is given by, 
Total area cleaned at each sweep of the blades = 

Thus, the total area cleaned at each sweep of the blades is 1254.96 cm2.
Q41: In the given figure arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaped region.

Ans: Given, arc with radius 14 cm each.
Area of sector is given by, 
From the figure area of shaded region is, 
⇒ A = 11×2×14 = 308cm2
Thus, area of shaded region is 308 cm2.
Q42: The radii of two circles are 19cm and 9cm respectively. Find the radius of the circle which has its circumference equal to the sum of the circumference of the two circles.
Ans: Given, radii of two circles as 19cm and 9 cm.
Circumference of the circle is given by C= 2πr.
C1 = circumference of the 1st circle
⇒ 2π(19) = 38π cm
C2 = circumference of the 2nd circle
⇒ 2π(19) = 18π cm
Circumference of the required circle = sum of circumferences of two circles
⇒ 2πr = 38π+18π cm
⇒ 2πr = 56π
⇒ r = 28cm
Thus, the radius of the required circle is 28 cm.
Q43: A car travels 0.99km distance in which each wheel makes 450 complete revolutions. Find the radius of its wheel
Ans: Given, distance travelled by a wheel in 450 complete revolutions = 0.99 km = 990m
Distance travelled in one revolution = 990/450 = 11/5.
Let r be the radius of the wheel.
Circumference of the circular field is given by, 2πr.
Q44: A sector is cut from a circle of diameter 21cm . If the angle of the sector is 150° find its area.
Ans: Given, diameter, d = 21cm
Thus, radius can be obtained as, r= 21/2 cm
Angle of sector = 150°
Area of the sector is given by, 
Hence, area of the sector is, 
⇒ A = 144.38 cm2.
Q45: In the given figure AOBCA represent a quadrant of area 9.625cm2. Calculate the area of the shaded portion.

Ans: Given, area of quadrant 9.625 cm2.
From the figure, OD = 2 cm and OA = 3.5 cm.
Area of the quadrant of a circle = 
Area of the shaded region = Area of the quadrant OACB − Area of the triangle BOD.
Area of the shaded region =
Hence, the area of the shaded region is 6.125 cm2.
[Question: 0]
 cm, then the area of the circle is
cm, then the area of the circle is
Short Answer Type Questions
Q1: Find the area of the shaded region if PQ = 24cm, PR = 7cm and O is the centre of the circle.
Ans: Given PQ = 24 cm and PR = 7 cm
Since QR is a diameter passing through the centre O of the circle
Angle of semi-circle, ∠RPQ = 90°

Diameter of the circle = 25cm
Thus radius, r = 25/2 cm
Area of the semi-circle = (1/2)πr2

From the given figure,
Area of the shaded region = Area of the semi-circle with O as centre and OQ as radius – area of ΔPQR
Hence, area of the shaded region can be calculated as,
Area of the shaded region =

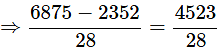
Area of the shaded region = 161.54cm2.
Q2: The perimeter of a sector of a circle of radius 5.7 m is 27.2 m.Calculate:
(i) The length of arc of the sector in cm.
Ans: Given radius, r = 5.7 m and perimeter = 27.2 m.
Then OA = OB = 5.7m
Now,
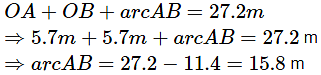
The length of the arc of the sector is 15.8 m.
(ii) The area of the sector in cm2 correct to the nearest cm2.
Ans: Area of sector OACB=
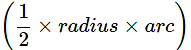
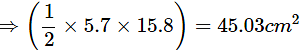
Area of sector correct to nearest cm2 = 45cm2
Q3: Find the area of the shaded region in the given figure where ABCD is a square of side 10cm and semi-circles are drawn with each side of the square as diameter. [π=3.14]
Ans: Given, side of square ABCD = 10 cm
Area of square ABCD = (side)2 = (10)2 = 100 cm2
Given that semicircle is drawn with side of square as diameter.
Diameter of semicircle = 10 cm.
Radius of semicircle = 5 cm
Area of semi-circle =
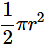
Area =
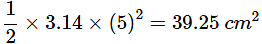
Area of 4 semi-circles – Area of shaded region = Area of square ABCD
∴Area of shaded region = Area of 4 semi-circles - Area of square ABCD
Area of shaded region = 4×39.25−100 = 57cm2
Q4: In the given figure ΔABC is an equilateral triangle inscribed in a circle of radius 4 cm and centre O. Show that the area of the shaded region is 4/3
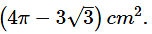
Ans: Given, ΔABC as an equilateral triangle inscribed in circle with radius, r = 4 cm.
In ΔOBD, Let BD = a, OB = 4cm

Area of shaded region = Area of sector OBPC – Area of ΔOBC
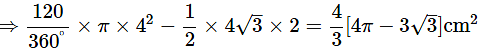
Q5: The radii of two circles are 8cm and 6cm respectively. Find the radius of the circle having its area equal to the sum of the areas of the two circles.
Ans: Given, radii of two circles, r1=8 cm and r2=6 cm.
Area of a circle is given by πr2
Let A1 = Area of the first circle

Hence, required radius = 10cm
Q6: A chord of a circle of radius 10cm subtends a right angle at the centre. Find the area of the corresponding: (Use π=3.14)
(i) minor sector
Ans: Given, radius of circle, r = 10cm subtending an angle 90∘ at the centre.
∴∠AOB = 90°.
Area of minor sector =
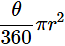
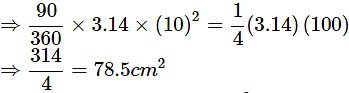
Area of minor sector is 78.5cm2.
(ii) major sector
Ans: Area of circle = πr2 = π(10)2
Area of major sector = Area of circle – Area of minor sector
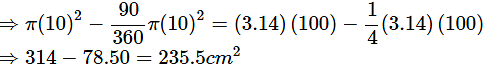
Area of major sector is 235.5 cm2.
(iii) minor segment
Ans: Area of minor segment = Area of minor sector OAB – Area of ΔOAB
Area of minor segment is 28.5 cm2.
(iv) major segment
Ans: Area of major segment = Area of the circle – Area of minor segment
Area of major segment is 285.5 cm2.
Q7: In Akshita’s house, there is a flower pot. The sum of radii of circular top and bottom of a flowerpot is 140 cm and the difference of their circumference is 88cm, find the diameter of the circular top and bottom.
Ans: Given, sum of radii of circular top and bottom = 140cm
Let radius of top = r cm
∴ Radius of bottom = (140−r)cm
Circumference of top = 2πr cm
Circumference of bottom = 2π(140−r)cm
Difference of circumference = [2πr−2π(140−r)]cm
By the given conditions in the problem,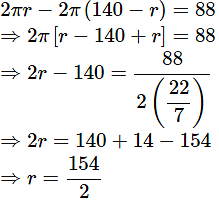
∴ Radius of top is obtained as 77cm
Diameter of top can be calculated as,
⇒ 2×77 = 154cm
Radius of bottom can be obtained as,
⇒ 140 r = 140 77
= 63cm
∴ Diameter of bottom 2×63=126cm .
Q8: A chord of a circle of radius 15cm subtends an angle of 60° at the centre. Find the area of the corresponding minor and major segments of the circle. (use π=3.14 and √3 =1.73 ).
Ans: Given, radius of circle, r = 15 cm subtending an angle 60° at centre.
∴∠AOB = 60°.
Area of a sector of a circle is given by, 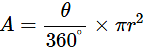
Area of minor segment = Area of minor sector OAB − area of ΔOAB
Area of major segment = Area of the circle – area of minor segment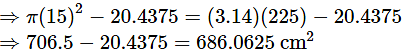
Area of minor segment is 20.4375 cm2 and area of major segment is 686.0625 cm2.
Q9: A round table cover has six equal designs as shown in the figure. If the radius of the cover is 28cm, find the cost of making the design at the rate of Rs.0.35 per cm2. (Use √3 =1.7)
Ans: Given, radius of cover, r = 28 cm. Table has six equal designs and the cost of making the design is Rs. 0.35 per cm2.
Area of equilateral triangle is given by, 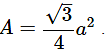
From the figure area of one design = 
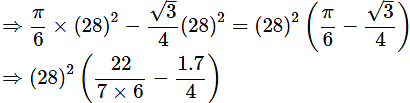
Total cost can be calculated as follows,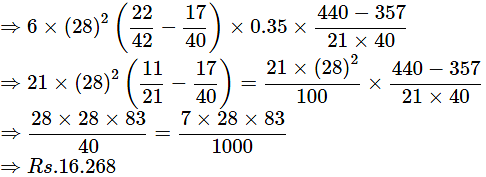
The total cost of making the design is Rs.16.268.
Q10: ABCD is a flower bed. If OA = 21m and DC = 14m. Find the area of the bed.
Ans: Given,
OA = R = 21m
OC = r = 14m
Area of the flower bed (i.e., shaded portion) = area of quadrant of a circle of radius R of the quadrant of a circle of radius r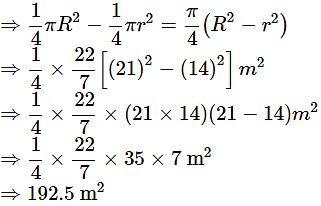
Hence, area of the flower bed is 192.5 m2.
Q11: In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) the length of the arc.
Ans: Given radius, r = 21 cm and angle θ = 60°.
Length of arc 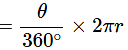
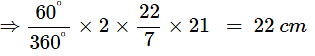
(ii) area of the sector formed by the arc.
Ans: Area of the sector = 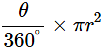
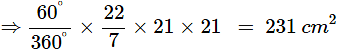
(iii) area of the segment formed by the corresponding chord
Ans: Area of segment formed by corresponding chord = 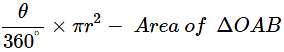
⇒ Area of segment =231− Area of ΔOAB …(1)
In right triangles OMA and OMB,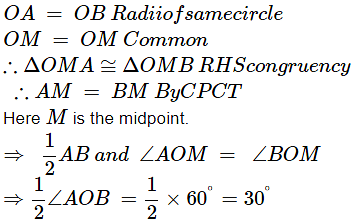
In right angled ΔOMA,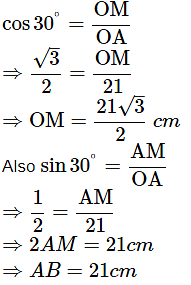
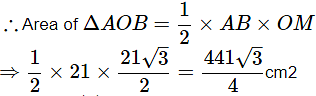
Using eq. (1),
Area of segment formed by corresponding chord = 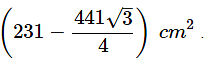
Q12: A chord of a circle of radius 15 cmsubtends an angle of 60° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and √3 = 1.73)
Ans: Given radius, r = 15 cm and angle θ = 60°
Area of minor sector can be obtained from 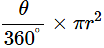
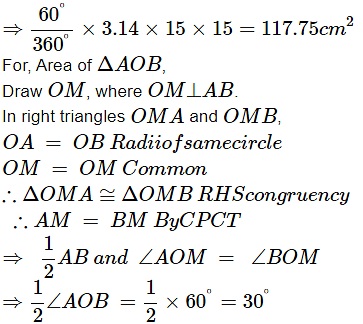
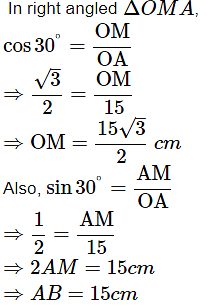
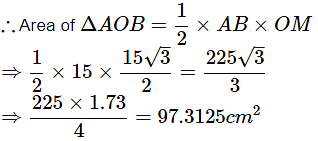
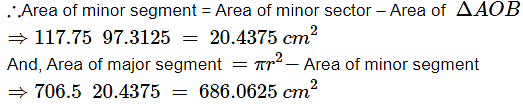
Q13: A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and √3 = 1.73)
Ans: Given radius, r = 12cm and angle θ = 120°.
Area of corresponding sector can be obtained by using the formula 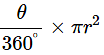

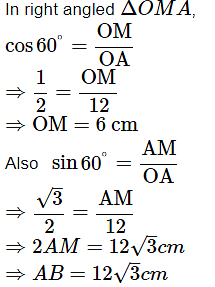

Area of corresponding segment = Area of corresponding sector – Area of ΔAOB
⇒150.72 62.28 = 88.44 cm2.
Q14: Find the area of the shaded region in figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
Ans: Given radius, r = 12cm and angle θ = 120°.
Area of corresponding sector can be obtained by using the formula 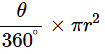

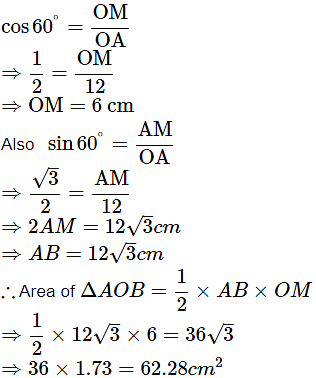
Area of corresponding segment = Area of corresponding sector – Area of ΔAOB
⇒150.72 62.28 = 88.44 cm2
Long Answer Type Questions
Q1: Three horses are tethered with 7m long ropes at the three corners of a triangular field having sides 20m, 34m and 42 m. Find the area of the plot which can be grazed by the horses. Also, find the area of the plot which remains ungrazed.
Ans: Given, length of ropes at the three corners, l = 33 m and the sides of the triangle as 20 m, 34 m and 42 m.
From the figure let, ∠A = θ1°, ∠B = θ2° and ∠C = θ3°
Area which can be grazed by three horses = Area of sector with central angle θ1° and radius 7 m+ Area of sector with central angle θ2° and radius 7 cm+ Area of sector with central angle θ3° and radius 7 cm
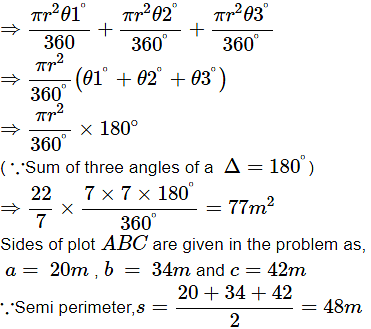
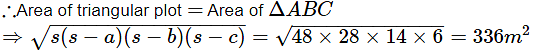
Area grazed by the horses = 77m2
∴ Ungrazed area can be calculated by subtracting area grazed by the horses from the area of the triangular plot.
⇒ Ungrazed area =(33677) = 259 m2
Q2: In the given figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56 m. If the corner of each circular flower bed is the point of enter section O of the diagonals of the square lawn. Find the sum of the areas of the lawn and the flower beds.
Ans: Given, side of square lawn = 56 m.
Area of the square lawn ABCD, A = (56)2
Let OA=OB=x
∴By Pythagoras theorem,
⇒ x2+x2 = 562
⇒ 2x2 = 56×56
⇒ x2 = 28×56
Again, area of sector

Substituting for x, we get
⇒ Area of sector
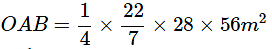
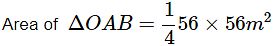
(Here, ∠AOB = 90° since square ABCD is divided into 4 right triangles)
∴ Area of flowerbed AB =
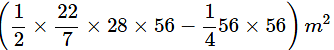
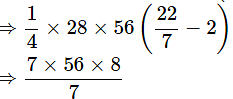
Area of flower bed AB = 448m2
Similarly, area of the other flowerbed = 448m2
Total area of the lawn and the flowerbeds = 56×56+448+448 = 4032m2
Q3: An elastic belt is placed round the rein of a pulley of radius 5 cm. One point on the belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from O. Find the length of the best that is in contact with the rim of the pulley. Also find the shaded area.
Ans: Given, radius of rein of pulley, OA = 5 cm.
OP = 10cm
Thus, cosθ= OA/OP

Length of the belt that is in contact with the rim of the pulley can be calculated by subtracting length of arc AB from Circumference of the rim.
Length of the belt
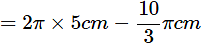
Length of the belt = 20/3 πcm
Now, area of sector OAQB=
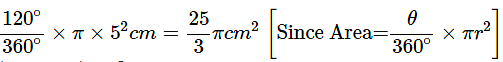

Area of quadrilateral OAPB is given by, 2(Area of ΔOAP) = 25√3cm2
Hence, shaded area can be obtained as,
Area of shaded region=
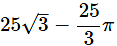
Hence, area of shaded region is 17.12 cm2.
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 11 Important Question Answers - Areas Related to Circles
| 1. What is the formula for the circumference of a circle? |  |
| 2. How do you find the area of a circle? |  |
| 3. What are the different parts of a circle? |  |
| 4. Can you explain the relationship between the radius and diameter of a circle? |  |
| 5. What is a tangent to a circle? |  |

|
Explore Courses for Class 10 exam
|

|

























