Overview: Statistics & Probability | Quantitative Aptitude for SSC CGL PDF Download
Statistics
- Statistics, in its simplest terms, can be described as the examination and manipulation of data. As previously discussed, the primary focus of statistics revolves around the analysis and computation of numerical data. Let's delve into a range of definitions of statistics provided by various authors.
- As per the Merriam-Webster dictionary, statistics can be defined as "organized information that represents the conditions of a population in a specific area, particularly information that can be expressed in numerical or other structured formats."
- Renowned statistician Sir Arthur Lyon Bowley offers a definition of statistics as "numerical statements of facts from any field of investigation, placed in correlation with one another."
Statistics Examples
Some of the real-life examples of statistics are:
- To find the mean of the marks obtained by each student in the class whose strength is 50. The average value here is the statistics of the marks obtained.
- Suppose you need to find how many members are employed in a city. Since the city is populated with 15 lakh people, hence we will take a survey here for 1000 people (sample). Based on that, we will create the data, which is the statistic.
Basics of Statistics
- The basics of statistics include the measure of central tendency and the measure of dispersion. The central tendencies are mean, median and mode and dispersions comprise variance and standard deviation.
- Mean is the average of the observations. Median is the central value when observations are arranged in order. The mode determines the most frequent observations in a data set.
- Variation is the measure of spread out of the collection of data. Standard deviation is the measure of the dispersion of data from the mean. The square of standard deviation is equal to the variance.
Mathematical Statistics
- Mathematical statistics is the application of Mathematics to Statistics, which was initially conceived as the science of the state — the collection and analysis of facts about a country: its economy, and, military, population, and so forth.
- Mathematical techniques used for different analytics include mathematical analysis, linear algebra, stochastic analysis, differential equation and measure-theoretic probability theory.
Types of Statistics
Basically, there are two types of statistics.
- Descriptive Statistics
- Inferential Statistics
In the case of descriptive statistics, the data or collection of data is described in summary. But in the case of inferential stats, it is used to explain the descriptive one. Both these types have been used on large scale.
Descriptive Statistics
The data is summarised and explained in descriptive statistics. The summarization is done from a population sample utilising several factors such as mean and standard deviation. Descriptive statistics is a way of organising, representing, and explaining a set of data using charts, graphs, and summary measures. Histograms, pie charts, bars, and scatter plots are common ways to summarise data and present it in tables or graphs. Descriptive statistics are just that: descriptive. They don’t need to be normalised beyond the data they collect.
Inferential Statistics
We attempt to interpret the meaning of descriptive statistics using inferential statistics. We utilise inferential statistics to convey the meaning of the collected data after it has been collected, evaluated, and summarised. The probability principle is used in inferential statistics to determine if patterns found in a study sample may be extrapolated to the wider population from which the sample was drawn. Inferential statistics are used to test hypotheses and study correlations between variables, and they can also be used to predict population sizes. Inferential statistics are used to derive conclusions and inferences from samples, i.e. to create accurate generalisations.
Statistics Formulas
The formulas that are commonly used in statistical analysis are given in the table below.
Summary Statistics
In Statistics, summary statistics are a part of descriptive statistics (Which is one of the types of statistics), which gives the list of information about sample data. We know that statistics deals with the presentation of data visually and quantitatively. Thus, summary statistics deals with summarizing the statistical information. Summary statistics generally deal with condensing the data in a simpler form, so that the observer can understand the information at a glance. Generally, statisticians try to describe the observations by finding:
- The measure of central tendency or mean of the locations, such as arithmetic mean.
- The measure of distribution shapes like skewness or kurtosis.
- The measure of dispersion such as the standard mean absolute deviation.
- The measure of statistical dependence such as correlation coefficient.
Summary Statistics Table
The summary statistics table is the visual representation of summarized statistical information about the data in tabular form.
For example, the blood group of 20 students in the class are O, A, B, AB, B, B, AB, O, A, B, B, AB, AB, O, O, B, A, AB, B, A.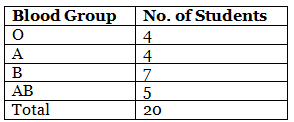
Thus, the summary statistics table shows that 4 students in the class have O blood group, 4 students have A blood group, 7 students in the class have B blood group and 5 students in the class have AB blood group. The summary statistics table is generally used to represent the big data related to population, unemployment, and the economy to be summarized systematically to interpret the accurate result.
Scope of Statistics
Statistics is used in many sectors such as psychology, geology, sociology, weather forecasting, probability and much more. The goal of statistics is to gain understanding from the data, it focuses on applications, and hence, it is distinctively considered as a mathematical science.
Methods in Statistics
The methods involve collecting, summarizing, analyzing, and interpreting variable numerical data. Here some of the methods are provided below.
- Data collection
- Data summarization
- Statistical analysis
What is Data in Statistics?
Data is a collection of facts, such as numbers, words, measurements, observations etc.
Types of Data
- Qualitative data- it is descriptive data.
- Example- She can run fast, He is thin.
- Quantitative data- it is numerical information.
- Example- An Octopus is an Eight legged creature.
Types of quantitative data
- Discrete data- has a particular fixed value. It can be counted
- Continuous data- is not fixed but has a range of data. It can be measured.
Representation of Data
There are different ways to represent data such as through graphs, charts or tables. The general representation of statistical data are:
- Bar Graph
- Pie Chart
- Line Graph
- Pictograph
- Histogram
- Frequency Distribution
Bar Graph
A Bar Graph represents grouped data with rectangular bars with lengths proportional to the values that they represent. The bars can be plotted vertically or horizontally.
Pie Chart
A type of graph in which a circle is divided into Sectors. Each of these sectors represents a proportion of the whole.
Line graph
The line chart is represented by a series of data points connected with a straight line.
The series of data points are called ‘markers.’
Pictograph
A pictorial symbol for a word or phrase, i.e. showing data with the help of pictures. Such as Apple, Banana & Cherry can have different numbers, and it is just a representation of data.
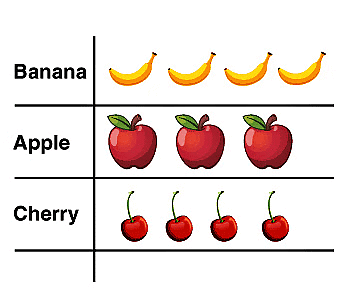
Histogram
A diagram is consisting of rectangles. Whose area is proportional to the frequency of a variable and whose width is equal to the class interval.
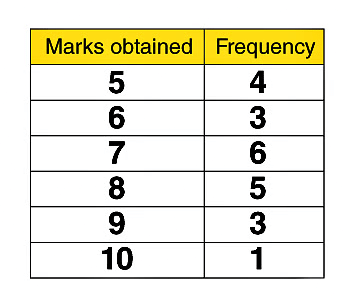
Frequency Distribution
The frequency of a data value is often represented by “f.” A frequency table is constructed by arranging collected data values in ascending order of magnitude with their corresponding frequencies.
Measures of Central Tendency
In Mathematics, statistics are used to describe the central tendencies of the grouped and ungrouped data. The three measures of central tendency are:
- Mean
- Median
- Mode
All three measures of central tendency are used to find the central value of the set of data.
Measures of Dispersion
In statistics, the dispersion measures help interpret data variability, i.e. to understand how homogenous or heterogeneous the data is. In simple words, it indicates how squeezed or scattered the variable is. However, there are two types of dispersion measures, absolute and relative. They are tabulated as below: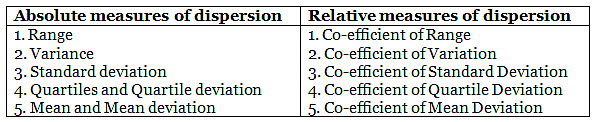
Skewness in Statistics
Skewness, in statistics, is a measure of the asymmetry in a probability distribution. It measures the deviation of the curve of the normal distribution for a given set of data.
The value of skewed distribution could be positive or negative or zero. Usually, the bell curve of normal distribution has zero skewness.
ANOVA Statistics
ANOVA Stands for Analysis of Variance. It is a collection of statistical models, used to measure the mean difference for the given set of data.
Degrees of freedom
In statistical analysis, the degree of freedom is used for the values that are free to change. The independent data or information that can be moved while estimating a parameter is the degree of freedom of information.
Applications of Statistics
Statistics have huge applications across various fields in Mathematics as well as in real life. Some of the applications of statistics are given below:
- Applied statistics, theoretical statistics and mathematical statistics
- Machine learning and data mining
- Statistics in society
- Statistical computing
- Statistics applied to the mathematics of the arts
Probability Terms and Definitions
- Sample Point: It denotes one of the possible outcomes. For example, in a deck of cards 4 of hearts is a sample point, similarly, the queen of clubs is a sample point.
- Experiment or Trial: A series of trials where the results are always unpredictable. For example, the tossing of a coin, picking a card from a deck of cards, rolling dice, etc.
- Random Experiment: This is an action where the result is uncertain, that is an experiment whose outcome cannot be predicted with certainty. For example, the throwing of dice or a coin, or selecting a card from a group of cards, etc.
- Sample Space: The set of all probable outcomes is termed sample space, It is denoted by S.
- Favourable outcomes: The favourable outcomes as the name signifies are the outcomes in which an individual is interested.
- Event: The possible subsets of the sample space linked with a random experiment are termed as the event of an experiment. Events are categorized based on their occurrence as follows;
- Equally likely events: Any set of events is said to be equally likely if they have an equal possibility to occur. Consider an example: When a dice is thrown the six(occurrences of 1 to 6) events are equally likely.
- Exhaustive events: A set of events is said to be exhaustive if at least one of them surely occurs whenever the experiment is executed. Consider the same above example of tossing the coin, here all the events from 1 to 6 are exhaustive.
- Mutually exclusive events: A set of events is said to be mutually exclusive if the occurrence of one of the events excludes/prevents the possibility of the occurrence of any additional event. Mutually exclusive events happen in the identical sample space. Suppose if A and B both are mutually exclusive events in the same sample space then P(A∩B) = 0.
- Independent Events: A set of events is said to be independent if the occurrence of an event is not influenced/ affected by the occurrence of the rest of the events. Independent events occur in different sample spaces. Suppose if A and B both are independent events in different sample spaces then P(A∩B) = P(A)P(B).
- Dependent Events: If the occurrence of one event influences or affects the probability of another event then the two events are said to be dependent. Now that we are familiar with the definitions and terms of probability let’s head towards the concept of probability, its definition, and other related concepts.
- Complimentary event: This type of event denotes the non-happening of events. The complement of an event P is the event, not P (or P’).
- Impossible Event: The event that cannot happen is called an impossible event. For example, in tossing a coin it is impossible to get both head and tail at an equal time.
Definition of Probability
The mathematical definition of probability of an event is defined as the ratio of the number of cases in its favor to the total number of cases. Consider S as a sample space and E be an event such that n(S) = n, n(E) = m and each outcome is equally likely. Then
Types of Probability
There are three important classes of probabilities:
- Theoretical Probability
- Experimental Probability
- Axiomatic Probability
Let us learn about three of them in the section:
Theoretical Probability
Theoretical Probability is based on the potential chances of something happening. The type of probability is principally based on the logic behind probability. For example, if a coin is tossed, the theoretical probability of getting a head or a tail will be ½ or o.5.
Experimental Probability
This type of probability is based on the observations of an experiment. The experimental probability can be determined based on the number of potential outcomes by the cumulative/total number of trials. For instance, if a coin is tossed 8 times and the head is recorded 4 times then, the experimental probability for heads is 4/8 or 1/2.
Axiomatic Probability
In axiomatic probability, a set of commands or assumptions are set which fits all types. These axioms are set by Kolmogorov and are called Kolmogorov’s three axioms. With the axiomatic method of probability, the chances of existence or non-existence of the events can be quantified.
Complementary Events
The possibility that there will be simply two outcomes that state that an event will occur or will not occur. For example, a person will visit or not visit your residence, getting a government job or not receiving a job, etc. are examples of complementary events. The complement of an event occurring is exactly the reverse of the probability of it not occurring. Some more additional examples are:
- It will rain or not rain tomorrow.
- The trainee will pass the examination or not pass.
- You win the quiz or you won’t win.
Probability Density Function
The Probability Density Function (PDF) is the probability function that is outlined for the density of a continuous random variable existing within a certain range of values. The PDF explains the normal distribution and how mean and deviation exist. The standard normal distribution is applied to build a database of statistics, which are frequently used in science to describe the real-valued variables, whose distribution is not identified.
Formulas of Probability
In probability examples, one thing that helps a lot are the formulas and theorem as probability sometimes gets a little confusing, so next will look at the formulas;
- P(A ∪ B) = P(A) + P(B) – P(A ∩ B).
- If A and B are mutually exclusive events i.e A ∩ B = ϕ, then P(A ∪ B) = P(A) + P(B).
- If A, B, and C are any three events then the formula for addition is given by;
- P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(A ∩ C) + P(A ∩ B ∩ C)
- If A, B, and C are any three events such that they are mutually exclusive then;
- P(A ∪ B ∪ C) = P(A) + P(B) + P(C)
Conditional Probability
Let A and B be any two events correlated with a random experiment. Then, the probability of occurrence of an event A with the condition that B has already occurred such that the probability of B is not equal to zero (P(B) ≠ 0), is called the conditional probability and denoted by P(A|B).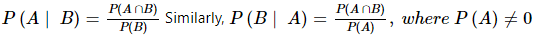
Key points for Conditional Probability
- Consider If
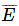 is the complement of the event E, then
is the complement of the event E, then 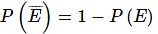
- For any event A, 0 ≤ P(A) ≤ 1, this is the range of probability.
- If A and B are independent events, then P(B|A)=P(B)∵P(A∩B)=P(A)×P(B)
Points to remember for Probability
If A and B are any two events in a random experiment then;
P(A ∩ B) = P(A | B) P(B), if P(B) ≠ 0.
P(A ∩ B) = P(B | A) P(A), if P(A) ≠ 0.
Important Probability Theorem and Distributions
Let us check out some of the important probability related theorems like the law of total probability, Bayes theorem, Binomial distribution and more in this section.
Law of Total Probability
Consider E1, E2, ….., En is n mutually exclusive and exhaustive events associated with a random experiment. If A is an event that occurs with E1 or E2 or … or En, then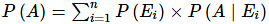
i.e P(A) = P(E1) × P(A | E1) + P(E2) × P(A | E2) + …. + P(En) × P(A |En).
Baye’s Theorem
Consider E1, E2, ….., En is n mutually exclusive and exhaustive events associated with a random experiment and let S be the sample space. Let A be an event that occurs together with any one of E1 or E2 or … or En such that P(A) ≠ 0. Then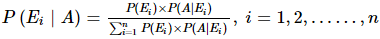
Binomial Distribution
If the probability of success of an event in a particular trial is p and that of the probability of failure is q = 1 – p, then the probability of exactly x successful event in n independent experiments is given by:
Mean and Variance of Binomial Distribution
The mean and variance of a binomial distribution B(n, p) is given by:Mean: 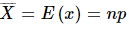
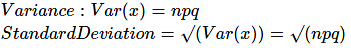
Some Concept of Mean, Median, and Mode
Mean is defined as the average value/expected value. Median is the central part of the data /observation after the arrangement. The mode is related to the highest occurred part in the provided observation. The relationship between mean, median, and mode is given by,
Mode = 3 Median – 2 Mean.
Probability Solved Problems
Learn more about probability with solved probability examples:
Example 1: Two dice are thrown simultaneously. Find the probability that the total of the numbers appearing on them is a prime number?
Solution: The sample space for the two dice thrown simultaneously is :
S = {(a, b)} {where a = 1, 2, ….., 6 and b = 1, 2, ……, 6}
⇒ n (S) = 36
Let A be a subset of S defined as A = {(a, b) | a + b is a prime no.
A = {(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), (6, 5)}
⇒ n (A) = 15
As we know that,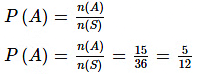
Example 2: If a fair die is rolled 4 times, then find the probability of exactly 2 sixes?
Solution: Given, A fair die is rolled 4 times.
Let p represent the probability of getting 6 = 1 / 6
and q represent the probability of not getting 6, that is = 1 – (1 / 6) = 5 / 6
As we know that, according to binomial distribution: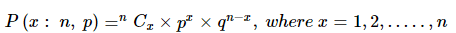
Here we get, n = 4, x = 2, p = 1 / 6 and q = 5 / 6.
Hence the probability of getting exactly 2 sixes when a fair dice is rolled 4 times is given by;a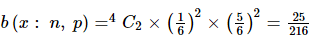
|
342 videos|298 docs|185 tests
|
FAQs on Overview: Statistics & Probability - Quantitative Aptitude for SSC CGL
| 1. What is the scope of statistics? |  |
| 2. What is the difference between descriptive and inferential statistics? |  |
| 3. How does probability relate to statistics? |  |
| 4. What are some common statistical techniques used in data analysis? |  |
| 5. How is statistics used in research studies? |  |





















