NCERT Solutions Class 11 Maths Chapter 6 - Permutations and Combinations
Q1: If 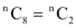 , find
, find 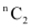 .
.
Ans: It is known that, 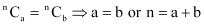
Therefore,
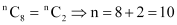

Q2: Determine n if (i)  (ii)
(ii)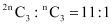
Ans: (i)
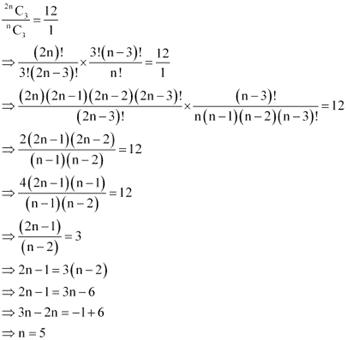
(ii)
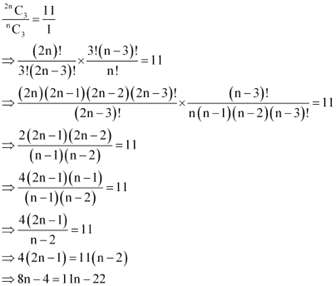
⇒ 11n – 8n = - 4+ 22
⇒ 3n = 18
⇒ n = 6
Q3: How many chords can be drawn through 21 points on a circle?
Ans: For drawing one chord on a circle, only 2 points are required.
To know the number of chords that can be drawn through the given 21 points on a circle, the number of combinations have to be counted.
Therefore, there will be as many chords as there are combinations of 21 points taken 2 at a time.
Thus, required number of chords = 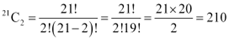
Q4: In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
Ans: A team of 3 boys and 3 girls is to be selected from 5 boys and 4 girls.
3 boys can be selected from 5 boys in 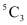 ways.
ways.
3 girls can be selected from 4 girls in 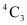 ways.
ways.
Therefore, by multiplication principle, number of ways in which a team of 3 boys and 3 girls can be selected

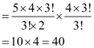
Q5: Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.
Ans: There are a total of 6 red balls, 5 white balls, and 5 blue balls.
9 balls have to be selected in such a way that each selection consists of 3 balls of each colour.
Here,
3 balls can be selected from 6 red balls in 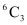 ways.
ways.
3 balls can be selected from 5 white balls in 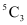 ways.
ways.
3 balls can be selected from 5 blue balls in 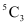 ways.
ways.
Thus, by multiplication principle, required number of ways of selecting 9 balls
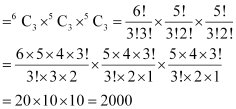
Q6: Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.
Ans: In a deck of 52 cards, there are 4 aces. A combination of 5 cards have to be made in which there is exactly one ace.
Then, one ace can be selected in 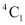 ways and the remaining 4 cards can be selected out of the 48 cards in
ways and the remaining 4 cards can be selected out of the 48 cards in 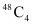 ways.
ways.
Thus, by multiplication principle, required number of 5 card combinations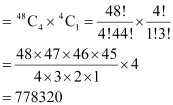
Q7: In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?
Ans: Out of 17 players, 5 players are bowlers.
A cricket team of 11 players is to be selected in such a way that there are exactly 4 bowlers.
4 bowlers can be selected in 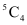 ways and the remaining 7 players can be selected out of the 12 players in
ways and the remaining 7 players can be selected out of the 12 players in 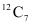 ways.
ways.
Thus, by multiplication principle, required number of ways of selecting cricket team 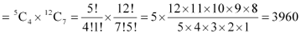
Q8: A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
Ans: There are 5 black and 6 red balls in the bag.
2 black balls can be selected out of 5 black balls in 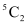 ways and 3 red balls can be selected out of 6 red balls in
ways and 3 red balls can be selected out of 6 red balls in 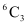 ways.
ways.
Thus, by multiplication principle, required number of ways of selecting 2 black and 3 red balls 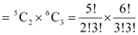

Q9: In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?
Ans: There are 9 courses available out of which, 2 specific courses are compulsory for every student.
Therefore, every student has to choose 3 courses out of the remaining 7 courses. This can be chosen in 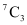 ways.
ways.
Thus, required number of ways of choosing the programme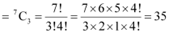
|
75 videos|238 docs|91 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 6 - Permutations and Combinations
| 1. How do permutations and combinations differ from each other? |  |
| 2. What is the formula for calculating permutations of objects? |  |
| 3. How can permutations and combinations be applied in real-life scenarios? |  |
| 4. What are the key differences between a permutation and a combination problem? |  |
| 5. Can permutations and combinations be used interchangeably in all situations? |  |

|
Explore Courses for Commerce exam
|

|











