Exercise 9.3- Straight Lines NCERT Solutions - Commerce PDF Download
Question 1: Reduce the following equations into slope-intercept form and find their slopes and the y-intercepts.
(i) x + 7y = 0
(ii) 6x + 3y – 5 = 0
(iii) y = 0
ANSWER : - (i) The given equation is x + 7y = 0.
It can be written as
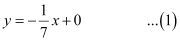
This equation is of the form y = mx + c, where 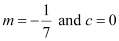 .
.
Therefore, equation (1) is in the slope-intercept form, where the slope and the y-intercept are 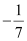 and 0 respectively.
and 0 respectively.
(ii) The given equation is 6x + 3y – 5 = 0.
It can be written as
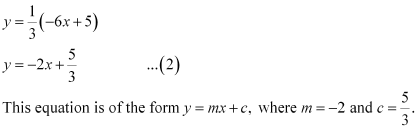
Therefore, equation (2) is in the slope-intercept form, where the slope and the y-intercept are –2 and  respectively.
respectively.
(iii) The given equation is y = 0.
It can be written as
y = 0.x + 0 … (3)
This equation is of the form y = mx + c, where m = 0 and c = 0.
Therefore, equation (3) is in the slope-intercept form, where the slope and the y-intercept are 0 and 0 respectively.
Question 2: Reduce the following equations into intercept form and find their intercepts on the axes.
(i) 3x + 2y – 12 = 0
(ii) 4x – 3y = 6
(iii) 3y + 2 = 0.
ANSWER : - (i) The given equation is 3x + 2y – 12 = 0.
It can be written as
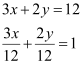
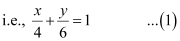
This equation is of the form 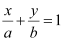 , where a = 4 and b = 6.
, where a = 4 and b = 6.
Therefore, equation (1) is in the intercept form, where the intercepts on the x and y axes are 4 and 6 respectively.
(ii) The given equation is 4x – 3y = 6.
It can be written as
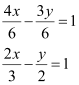
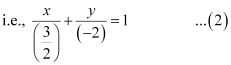
This equation is of the form 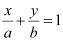 , where a =
, where a = 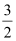 and b = –2.
and b = –2.
Therefore, equation (2) is in the intercept form, where the intercepts on the x and y axes are  and –2 respectively.
and –2 respectively.
(iii) The given equation is 3y + 2 = 0.
It can be written as
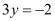
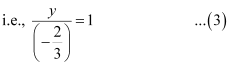
This equation is of the form 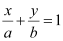 , where a = 0 and b =
, where a = 0 and b = 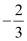 .
.
Therefore, equation (3) is in the intercept form, where the intercept on the y-axis is 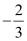 and it has no intercept on the x-axis.
and it has no intercept on the x-axis.
Question 3: Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).
ANSWER : - The given equation of the line is 12(x + 6) = 5(y – 2).
⇒ 12x + 72 = 5y – 10
⇒12x – 5y + 82 = 0 … (1)
On comparing equation (1) with general equation of line Ax + By + C = 0, we obtain A = 12, B = –5, and C = 82.
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by 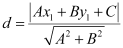 .
.
The given point is (x1, y1) = (–1, 1).
Therefore, the distance of point (–1, 1) from the given line
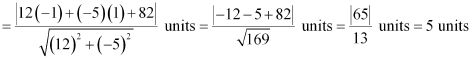
Question 4: Find the points on the x-axis, whose distances from the line 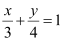 are 4 units.
are 4 units.
ANSWER : - The given equation of line is
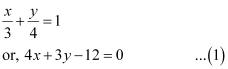
On comparing equation (1) with general equation of line Ax + By + C = 0, we obtain A = 4, B = 3, and C = –12.
Let (a, 0) be the point on the x-axis whose distance from the given line is 4 units.
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by 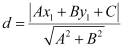 .
.
Therefore,
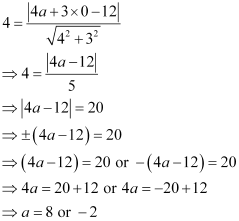
Thus, the required points on the x-axis are (–2, 0) and (8, 0).
Question 5: Find the distance between parallel lines
(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0
(ii) l (x + y) + p = 0 and l (x + y) – r = 0
ANSWER : - It is known that the distance (d) between parallel lines Ax + By + C1 = 0 and Ax + By + C2 = 0 is given by 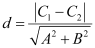 .
.
(i) The given parallel lines are 15x + 8y – 34 = 0 and 15x + 8y +31 = 0.
Here, A = 15, B = 8, C1 = –34, and C2 = 31.
Therefore, the distance between the parallel lines is
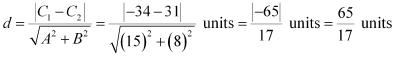
(ii) The given parallel lines are l (x + y) + p = 0 and l (x + y) – r = 0.
lx + ly + p = 0 and lx + ly – r = 0
Here, A = l, B = l, C1 = p, and C2 = –r.
Therefore, the distance between the parallel lines is
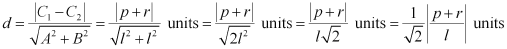
Question 6: Find equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (–2, 3).
ANSWER : - The equation of the given line is
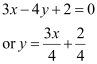
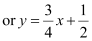 , which is of the form y = mx + c
, which is of the form y = mx + c
∴ Slope of the given line 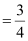
It is known that parallel lines have the same slope.
∴ Slope of the other line = 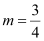
Now, the equation of the line that has a slope of 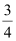 and passes through the point (–2, 3) is
and passes through the point (–2, 3) is
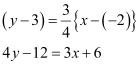
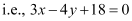
Question 7: Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept 3.
ANSWER : - The given equation of line is 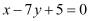 .
.
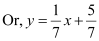 , which is of the form y = mx + c
, which is of the form y = mx + c
∴Slope of the given line 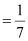
The slope of the line perpendicular to the line having a slope of 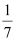 is
is 
The equation of the line with slope –7 and x-intercept 3 is given by
y = m (x – d)
⇒ y = –7 (x – 3)
⇒ y = –7x 21
⇒ 7x + y = 21
Question 8: Find angles between the lines 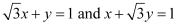
ANSWER : - The given lines are 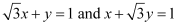 .
.
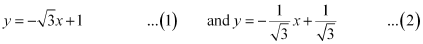
The slope of line (1) is 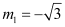 , while the slope of line (2) is
, while the slope of line (2) is 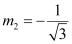 .
.
The acute angle i.e., θ between the two lines is given by
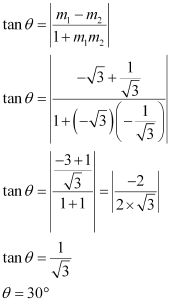
Thus, the angle between the given lines is either 30° or 180° – 30° = 150°.
Question 9: The line through the points (h, 3) and (4, 1) intersects the line 7x – 9y – 19 = 0. at right angle. Find the value of h.
ANSWER : - The slope of the line passing through points (h, 3) and (4, 1) is
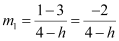
The slope of line 7x – 9y – 19 = 0 or 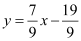 is
is 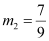 .
.
It is given that the two lines are perpendicular.
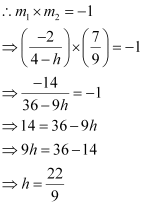
Thus, the value of h is 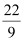 .
.
Question 10: Prove that the line through the point (x1, y1) and parallel to the line Ax + By + C = 0 is A (x –x1) + B (y – y1) = 0.
ANSWER : - The slope of line Ax + By C = 0 or 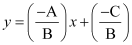 is
is 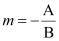
It is known that parallel lines have the same slope.
∴ Slope of the other line = 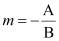
The equation of the line passing through point (x1, y1) and having a slope 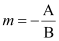 is
is
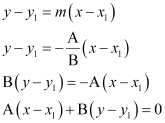
Hence, the line through point (x1, y1) and parallel to line Ax + By + C = 0 is
A (x –x1) + B (y – y1) = 0
Question 11: Two lines passing through the point (2, 3) intersects each other at an angle of 60°. If slope of one line is 2, find equation of the other line.
ANSWER : - It is given that the slope of the first line, m1 = 2.
Let the slope of the other line be m2.
The angle between the two lines is 60°.
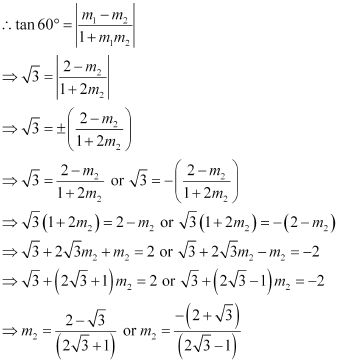
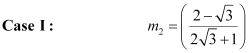
The equation of the line passing through point (2, 3) and having a slope of 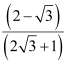 is
is
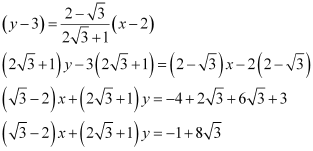
In this case, the equation of the other line is 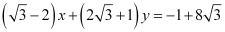 .
.
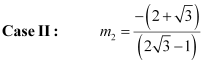
The equation of the line passing through point (2, 3) and having a slope of 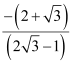 is
is
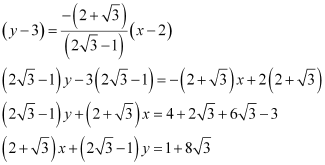
In this case, the equation of the other line is 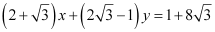 .
.
Thus, the required equation of the other line is 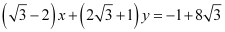 or
or 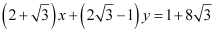 .
.
Question 12: Find the equation of the right bisector of the line segment joining the points (3, 4) and (–1, 2).
ANSWER : - The right bisector of a line segment bisects the line segment at 90°.
The end-points of the line segment are given as A (3, 4) and B (–1, 2).
Accordingly, mid-point of AB 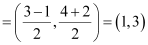
Slope of AB 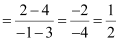
∴Slope of the line perpendicular to AB = 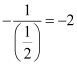
The equation of the line passing through (1, 3) and having a slope of –2 is
(y – 3) = –2 (x – 1)
y – 3 = –2x + 2
2x + y = 5
Thus, the required equation of the line is 2x + y = 5.
Question 13: Find the coordinates of the foot of perpendicular from the point (–1, 3) to the line 3x – 4y – 16 = 0.
ANSWER : - Let (a, b) be the coordinates of the foot of the perpendicular from the point (–1, 3) to the line 3x – 4y – 16 = 0.
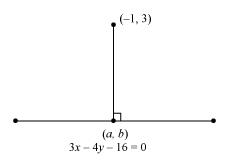
Slope of the line joining (–1, 3) and (a, b), m1
Slope of the line 3x – 4y – 16 = 0 or 
Since these two lines are perpendicular, m1m2 = –1

Point (a, b) lies on line 3x – 4y = 16.
∴3a – 4b = 16 … (2)
On solving equations (1) and (2), we obtain
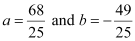
Thus, the required coordinates of the foot of the perpendicular are  .
.
Question 14: The perpendicular from the origin to the line y = mx + c meets it at the point (–1, 2). Find the values of m and c.
ANSWER : - The given equation of line is y = mx + c.
It is given that the perpendicular from the origin meets the given line at (–1, 2).
Therefore, the line joining the points (0, 0) and (–1, 2) is perpendicular to the given line.
∴Slope of the line joining (0, 0) and (–1, 2) 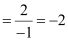
The slope of the given line is m.
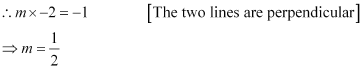
Since point (–1, 2) lies on the given line, it satisfies the equation y = mx + c.
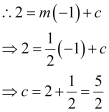
Thus, the respective values of m and c are 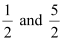 .
.
Question 15: If p and q are the lengths of perpendiculars from the origin to the lines x cos θ – y sin θ = k cos 2θ and x sec θ + y cosec θ = k, respectively, prove that p2 + 4q2 = k2
ANSWER : - The equations of given lines are
x cos θ – y sinθ = k cos 2θ … (1)
x secθ + y cosec θ= k … (2)
The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by 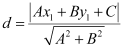 .
.
On comparing equation (1) to the general equation of line i.e., Ax + By + C = 0, we obtain A = cosθ, B = –sinθ, and C = –k cos 2θ.
It is given that p is the length of the perpendicular from (0, 0) to line (1).

On comparing equation (2) to the general equation of line i.e., Ax + By + C = 0, we obtain A = secθ, B = cosecθ, and C = –k.
It is given that q is the length of the perpendicular from (0, 0) to line (2).
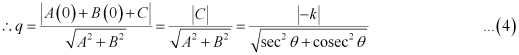
From (3) and (4), we have
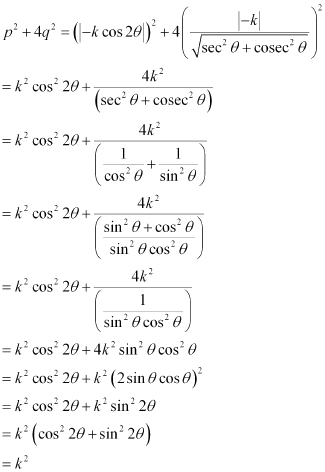
Hence, we proved that p2 + 4q2 = k2.
Question 16: In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
ANSWER : - Let AD be the altitude of triangle ABC from vertex A.
Accordingly, AD⊥BC
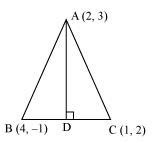
The equation of the line passing through point (2, 3) and having a slope of 1 is
(y – 3) = 1(x – 2)
⇒ x – y + 1 = 0
⇒ y – x = 1
Therefore, equation of the altitude from vertex A = y – x = 1.
Length of AD = Length of the perpendicular from A (2, 3) to BC
The equation of BC is
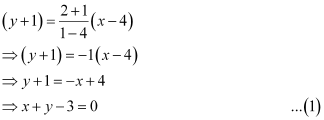
The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by 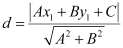 .
.
On comparing equation (1) to the general equation of line Ax + By + C = 0, we obtain A = 1, B = 1, and C = –3.
∴Length of AD 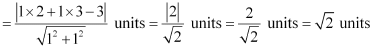
Thus, the equation and the length of the altitude from vertex A are y – x = 1 and 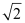 units respectively.
units respectively.
Question 17: If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 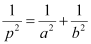 .
.
ANSWER : - It is known that the equation of a line whose intercepts on the axes are a and b is
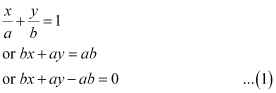
The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by 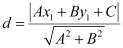 .
.
On comparing equation (1) to the general equation of line Ax + By + C = 0, we obtain A = b, B = a, and C = –ab.
Therefore, if p is the length of the perpendicular from point (x1, y1) = (0, 0) to line (1), we obtain
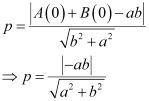
On squaring both sides, we obtain
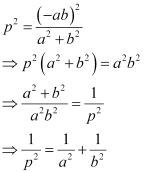
Hence, we showed that 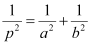 .
.
FAQs on Exercise 9.3- Straight Lines NCERT Solutions - Commerce
| 1. What is the significance of exercise 9.3 in NCERT Solutions for Straight Lines JEE? |  |
| 2. How can I use NCERT Solutions Exercise 9.3 to prepare for JEE? |  |
| 3. Are the solutions in NCERT Exercise 9.3 for Straight Lines JEE accurate? |  |
| 4. Can I solely rely on NCERT Exercise 9.3 for Straight Lines JEE preparation? |  |
| 5. How can I make the most of NCERT Exercise 9.3 for Straight Lines JEE? |  |














