NCERT Solutions Class 11 Maths Chapter 10 - Conic Sections
Question 1: If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.
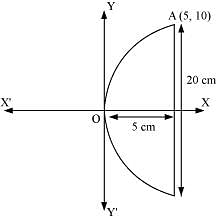
ANSWER : - The origin of the coordinate plane is taken at the vertex of the parabolic reflector in such a way that the axis of the reflector is along the positive x-axis.
This can be diagrammatically represented as
The equation of the parabola is of the form y2 = 4ax (as it is opening to the right).
Since the parabola passes through point A (10, 5), 102 = 4a(5)
⇒ 100 = 20a
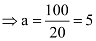
Therefore, the focus of the parabola is (a, 0) = (5, 0), which is the mid-point of the diameter.
Hence, the focus of the reflector is at the mid-point of the diameter.
Question 2: An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?
ANSWER : - The origin of the coordinate plane is taken at the vertex of the arch in such a way that its vertical axis is along the positive y-axis.
This can be diagrammatically represented as
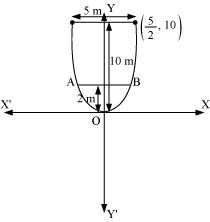
The equation of the parabola is of the form x2 = 4ay (as it is opening upwards).
It can be clearly seen that the parabola passes through point 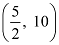 .
.
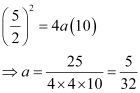
Therefore, the arch is in the form of a parabola whose equation is 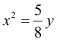 .
.
When y = 2 m, 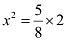
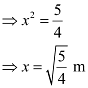
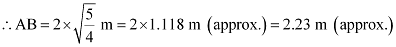
Hence, when the arch is 2 m from the vertex of the parabola, its width is approximately 2.23 m.
Question 3: The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
ANSWER : - The vertex is at the lowest point of the cable. The origin of the coordinate plane is taken as the vertex of the parabola, while its vertical axis is taken along the positive y-axis. This can be diagrammatically represented as
Here, AB and OC are the longest and the shortest wires, respectively, attached to the cable.
DF is the supporting wire attached to the roadway, 18 m from the middle.
Here, AB = 30 m, OC = 6 m, and 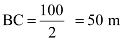 .
.
The equation of the parabola is of the form x2 = 4ay (as it is opening upwards).
The coordinates of point A are (50, 30 – 6) = (50, 24).
Since A (50, 24) is a point on the parabola,
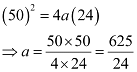
∴Equation of the parabola, 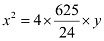 or 6x2 = 625y
or 6x2 = 625y
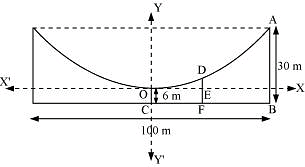
The x-coordinate of point D is 18.
Hence, at x = 18,
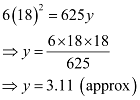
∴DE = 3.11 m
DF = DE EF = 3.11 m 6 m = 9.11 m
Thus, the length of the supporting wire attached to the roadway 18 m from the middle is approximately 9.11 m.
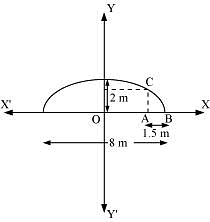
Question 4: An arch is in the form of a semi-ellipse. It is 8 m wide and 2 m high at the centre. Find the height of the arch at a point 1.5 m from one end.
ANSWER : - Since the height and width of the arc from the centre is 2 m and 8 m respectively, it is clear that the length of the major axis is 8 m, while the length of the semi-minor axis is 2 m.
The origin of the coordinate plane is taken as the centre of the ellipse, while the major axis is taken along the x-axis. Hence, the semi-ellipse can be diagrammatically represented as
The equation of the semi-ellipse will be of the form 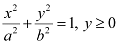 , where a is the semi-major axis
, where a is the semi-major axis
Accordingly, 2a = 8 ⇒ a = 4
b = 2
Therefore, the equation of the semi-ellipse is 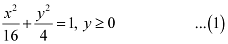
Let A be a point on the major axis such that AB = 1.5 m.
Draw AC⊥ OB.
OA = (4 – 1.5) m = 2.5 m
The x-coordinate of point C is 2.5.
On substituting the value of x with 2.5 in equation (1), we obtain
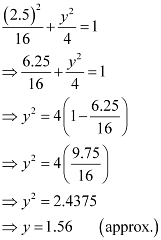
∴AC = 1.56 m
Thus, the height of the arch at a point 1.5 m from one end is approximately 1.56 m.
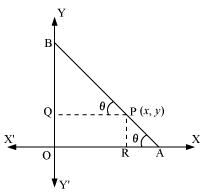
Question 5: A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.
ANSWER : - Let AB be the rod making an angle θ with OX and P (x, y) be the point on it such that AP = 3 cm.
Then, PB = AB – AP = (12 – 3) cm = 9 cm [AB = 12 cm]
From P, draw PQ⊥OY and PR⊥OX.
In ΔPBQ, 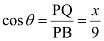
In ΔPRA, 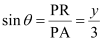
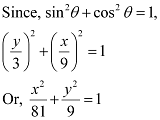
Thus, the equation of the locus of point P on the rod is 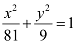 .
.
Question 6: Find the area of the triangle formed by the lines joining the vertex of the parabola x2 = 12y to the ends of its latus rectum.
ANSWER : - The given parabola is x2 = 12y.
On comparing this equation with x2 = 4ay, we obtain 4a = 12 ⇒ a = 3
∴The coordinates of foci are S (0, a) = S (0, 3)
Let AB be the latus rectum of the given parabola.
The given parabola can be roughly drawn as
At y = 3, x2 = 12 (3) ⇒ x2 = 36 ⇒ x = ±6
∴The coordinates of A are (–6, 3), while the coordinates of B are (6, 3).
Therefore, the vertices of ΔOAB are O (0, 0), A (–6, 3), and B (6, 3).
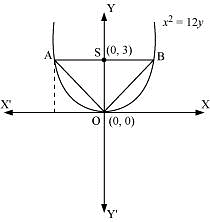
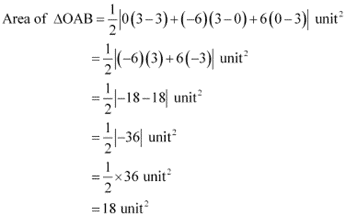
Thus, the required area of the triangle is 18 unit2.
Question 7: A man running a racecourse notes that the sum of the distances from the two flag posts form him is always 10 m and the distance between the flag posts is 8 m. find the equation of the posts traced by the man.
ANSWER : - Let A and B be the positions of the two flag posts and P(x, y) be the position of the man. Accordingly, PA + PB = 10.
We know that if a point moves in a plane in such a way that the sum of its distances from two fixed points is constant, then the path is an ellipse and this constant value is equal to the length of the major axis of the ellipse.
Therefore, the path described by the man is an ellipse where the length of the major axis is 10 m, while points A and B are the foci.
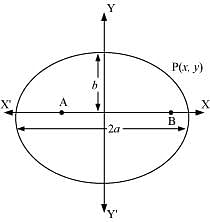
Taking the origin of the coordinate plane as the centre of the ellipse, while taking the major axis along the x-axis, the ellipse can be diagrammatically represented as
The equation of the ellipse will be of the form 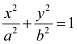 , where a is the semi-major axis
, where a is the semi-major axis
Accordingly, 2a = 10 ⇒ a = 5
Distance between the foci (2c) = 8
⇒ c = 4
On using the relation 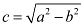 , we obtain
, we obtain
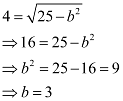
Thus, the equation of the path traced by the man is 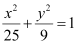 .
.
Question 8: An equilateral triangle is inscribed in the parabola y2 = 4 ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
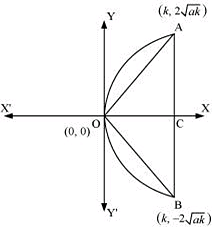
ANSWER : - Let OAB be the equilateral triangle inscribed in parabola y2 = 4ax.
Let AB intersect the x-axis at point C.
Let OC = k
From the equation of the given parabola, we have 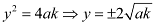
∴The respective coordinates of points A and B are 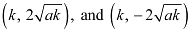
AB = CA+ CB = 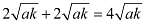
Since OAB is an equilateral triangle, OA2 = AB2.
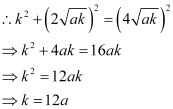
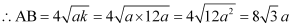
Thus, the side of the equilateral triangle inscribed in parabola y2 = 4 ax is 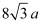 .
.
|
75 videos|238 docs|91 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 10 - Conic Sections
| 1. What are conic sections? |  |
| 2. How are conic sections used in real life? |  |
| 3. What is the equation of a circle in conic sections? |  |
| 4. How do conic sections relate to algebraic equations? |  |
| 5. How can one identify the type of conic section from its equation? |  |

|
Explore Courses for Commerce exam
|

|

















