Tips and Tricks for Cubes & Cuboids | IPMAT Mock Test Series - Commerce PDF Download
Any cube has the following characteristic:
- 6 faces
- 12 edges
- 8 corners
Unpainted CUBE
- Equal Cuts: When each side of a cube is divided into n parts, each side of the resulting smaller cubes is 1/n of the original side. This method creates n3 smaller cubes.
- Unequal Cuts: If the cube's sides are cut unequally, with L cuts along the length, 'L+1' parts along the breadth, and H cuts along the height, the total number of pieces formed is (L+1)(B+1)(H+1).
Painted CUBE
A cube painted on all its faces yields three types of cubes when cut along the length, breadth, and height.
- Zero Painted Face: At the center of the larger cube.
- Single Painted Face: On the face of the larger cube.
- Two Painted Face: Along the edge of the larger cube.
- Three Painted Face: At the corner of the larger cube.
Single Painted Face
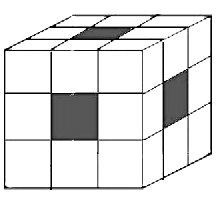
Two Painted Face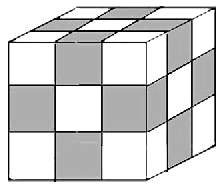
Three Painted Face
In addition, we have to note that there can be no smaller cube which has all the face painted.
Cube( n x n x n ) Cut into Cubes :
- Total Number of Cubes: n3
- Zero Painted Face : (n-2)3
- Single Painted Face : 6(n-2)^3
- Two Painted Face: 12(n-2)
- Three Painted Face: 8
Cuboid( p x q x r ) Cut into Cubes :
- Total Number of Cubes: p x q x r
- Zero Painted Face: (p-2) x (q-2) x (r-2)
- Single Painted Face: 2(p-2)(q-2)+ 2(q-2)(r-2)+2(r-2)p-2)
- Two Painted Face: 4(p-2) +4(q-2)+4(r-2)
- Three Painted Face: 8
So, the above results represent the number of cubes which can be formed by making the equal length cutting. The table below mentions direct results which can come handy in Cube Questions for CAT Exam.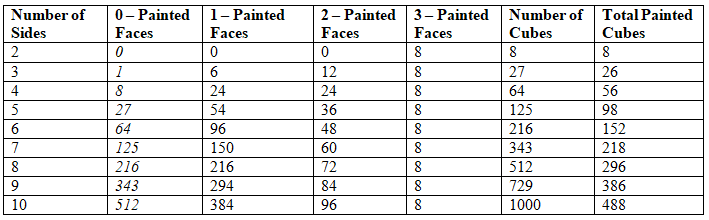
Examples
Example 1: Find the maximum number of smaller pieces with 19 cuts on a cube?
Sol: Since, equal number of cuts in each direction gives the maximum number of pieces. So, we can split 19 cuts into 6,6 and 7.
Therefore, by the number of pieces formed = (6 + 1)(6 + 1)(7 + 1) pieces = 7 * 7 * 8 = 392 pieces
Example 2: Find the least number of cuts required which can cut a cube into 24 identical pieces?
Sol: First of all, if we have 24 pieces, factorize the number it into three numbers such that all the factors are greater than 1.
⇒ 24 = 2 x 2 x 2 x 3
⇒ 24 = 2 x 3 x 4
Therefore, by using the above mentioned formulas, the number of pieces along different lengths leads to formation of (L+1)(B+1)(H+1) cubes. Hence, by comparing we get L = 1 , B = 2 and H = 3. Therefore, number of cuts is equal to (1 + 2 + 3) cuts or 6 cuts
Example 3: A cube of side 20 cm is of blue color with a 4 cm wide yellow strip along all the sides on all the faces. The cube is then cut into 125 smaller equal size cubes
(1) How many cubes have three yellow faces each?
(2) How many cubes have one face blue and an adjacent face yellow?
(3) How many cubes have at least one face colored?
(4) How many cubes have at least two yellow faces each?
First of all, the cube is cut into 125 smaller cubes of equal size. So, we get a stack of cubes in the figure below: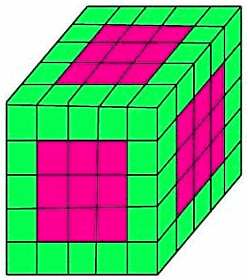
Hence, we start by analyzing the figure. 5 horizontal stacked layers are present in the figure
(1): Cubes with corners painted yellow.
Since, all the cubes with painted yellow face are at corner. Therefore, 3 Yellow Painted Face Cubes are 8 in number
(2): One face blue and an adjacent face yellow
Since, there would be no cube having one face blue and an adjacent face yellow as all the yellow painted cubes got paint on at least 2 faces. Therefore, the answer is zero
(3): At least one face colored
Because, the number of cubes with no painted face, (n-2)3 = (5-2)3 = 27
Therefore, there are (125 – 27) = 98 cubes which have at least one face colored.
(4): At least two yellow faces
So, by subtracting the cubes with blue painted face and cubes with no painted face from total number of cubes
Therefore, number of cubes of such types = 125 – (9 x 6) – 27 = 44
|
9 videos|39 docs|10 tests
|
FAQs on Tips and Tricks for Cubes & Cuboids - IPMAT Mock Test Series - Commerce
| 1. What is the difference between a cube and a cuboid? |  |
| 2. How can I calculate the volume of a cube? |  |
| 3. Can a cube and a cuboid have the same volume? |  |
| 4. How do I find the surface area of a cuboid? |  |
| 5. Can a cube and a cuboid have the same surface area? |  |





















