Practice Questions: Games and Tournaments- 1 | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
Direction
Pulak, Qasim, Ritesh, and Suresh participated in a tournament comprising of eight rounds. In each round, they formed two pairs, with each of them being in exactly one pair. The only restriction in the pairing was that the pairs would change in successive rounds. For example, if Pulak formed a pair with Qasim in the first round, then he would have to form a pair with Ritesh or Suresh in the second round. He would be free to pair with Qasim again in the third round. In each round, each pair decided whether to play the game in that round or not. If they decided not to play, then no money was exchanged between them. If they decided to play, they had to bet either ₹1 or ₹2 in that round. For example, if they chose to bet ₹2, then the player winning the game got ₹2 from the one losing the game.
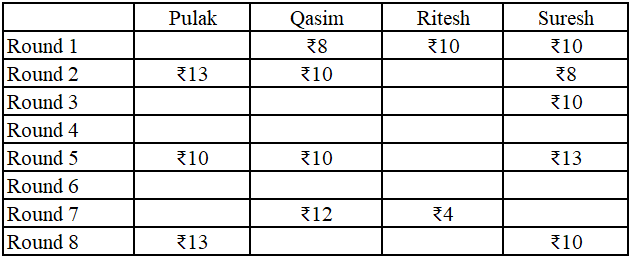
At the beginning of the tournament, the players had ₹10 each. The following table shows partial information about the amounts that the players had at the end of each of the eightrounds. It shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds. For example, Suresh had ₹10 at the end of Rounds 1, 3 and 8 and not after any of the other rounds. The maximum amount that he had at the end of any round was ₹13 (at the end of Round 5), and the minimum amount he had at the end of any round was ₹8 (at the end of Round 2). At the end of all other rounds, he must have had either ₹9, ₹11, or ₹12.
It was also known that Pulak and Qasim had the same amount of money with them at the end of Round 4.
Q1: What BEST can be said about the amount of money that Ritesh had with him at the end of Round 8?
(a) ₹4 or ₹5
(b) Exactly ₹5
(c) ₹5 or ₹6
(d) Exactly ₹6
Ans: (d)
Sol:
Its given that the table shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds, which means that in Pulak's column the numbers possible are 11 or 12 only, similarly in Qasim's column numbers possible are only 9 or 11 only, similarly in Ritesh's column numbers possible are 5,6,7,8 or 9 only and in Suresh's column numbers possible are 9,11 or 12 only.
Everyone started with 10 rupees and the total amount,i.e., 40 in each round remains the same. So we get the following table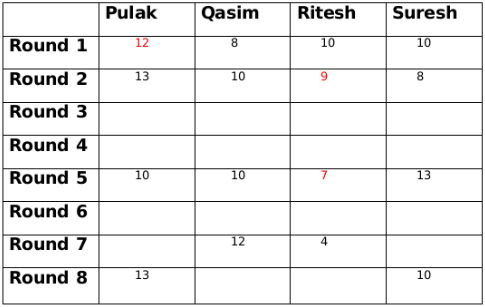 We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
As per the information given in the set the only possible amount with Qasim at the end of round 6 is 11.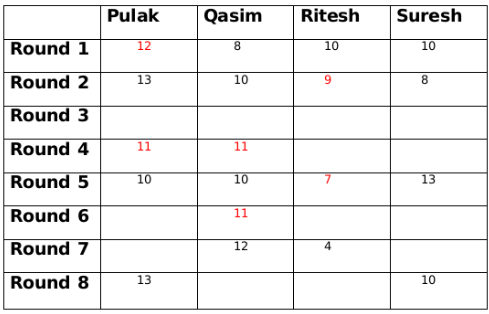 Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.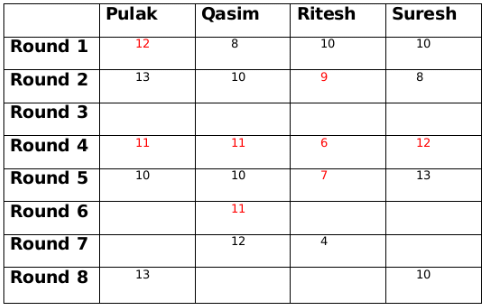 Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Qasim at the end of round 3 is either 9 or 11. If the amount is 9 then either amount with Ritesh has to be 10 or amount with Pulak has to to be 14, both of which is not possible. Therefore, amount with Qasim at the end of round 3 is 11.
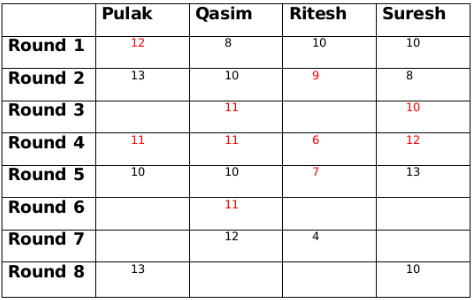
Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
The only possible amount with Qasim at the end of round 8 can be 11 and therefore the amount at the end of round 8 with Ritesh will be 6.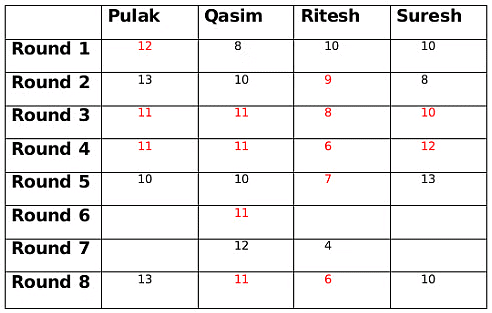 The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.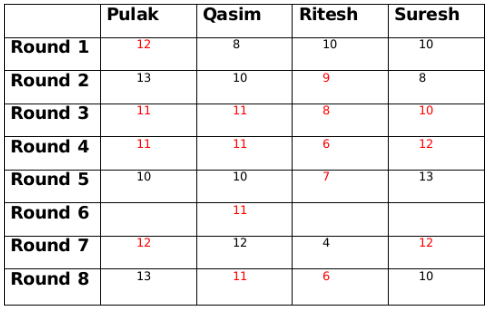 The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
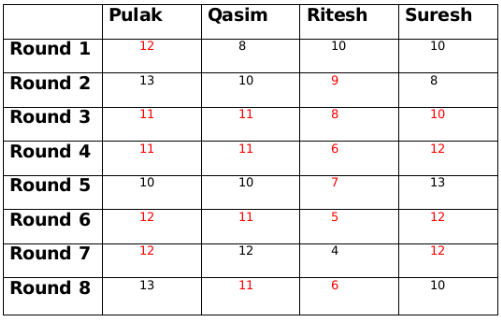
If the amount with Suresh at the end of round 6 is 11 then the amount with Pulak at the end of round 6 will be 13 which is not possible. Therefore the amount with Suresh at the end of round 6 is 12 and the amount with Pulak at the end of round 6 is 12.
Q2: What BEST can be said about the amount of money that Pulak had with him at the end of Round 6?
(a) Exactly ₹12
(b) Exactly ₹11
(c) ₹12 or ₹13
(d) ₹11 or ₹12
Ans: (a)
Sol:
Its given that the table shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds, which means that in Pulak's column the numbers possible are 11 or 12 only, similarly in Qasim's column numbers possible are only 9 or 11 only, similarly in Ritesh's column numbers possible are 5,6,7,8 or 9 only and in Suresh's column numbers possible are 9,11 or 12 only.
Everyone started with 10 rupees and the total amount,i.e., 40 in each round remains the same. So we get the following table We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
As per the information given in the set the only possible amount with Qasim at the end of round 6 is 11. Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4. Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Qasim at the end of round 3 is either 9 or 11. If the amount is 9 then either amount with Ritesh has to be 10 or amount with Pulak has to to be 14, both of which is not possible. Therefore, amount with Qasim at the end of round 3 is 11.

Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
The only possible amount with Qasim at the end of round 8 can be 11 and therefore the amount at the end of round 8 with Ritesh will be 6. The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7. The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
If the amount with Suresh at the end of round 6 is 11 then the amount with Pulak at the end of round 6 will be 13 which is not possible. Therefore the amount with Suresh at the end of round 6 is 12 and the amount with Pulak at the end of round 6 is 12.

Q3: How much money (in ₹) did Ritesh have at the end of Round 4?
Ans: 6
Sol:
Its given that the table shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds, which means that in Pulak's column the numbers possible are 11 or 12 only, similarly in Qasim's column numbers possible are only 9 or 11 only, similarly in Ritesh's column numbers possible are 5,6,7,8 or 9 only and in Suresh's column numbers possible are 9,11 or 12 only.
Everyone started with 10 rupees and the total amount,i.e., 40 in each round remains the same. So we get the following table We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
As per the information given in the set the only possible amount with Qasim at the end of round 6 is 11. Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4. Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Qasim at the end of round 3 is either 9 or 11. If the amount is 9 then either amount with Ritesh has to be 10 or amount with Pulak has to to be 14, both of which is not possible. Therefore, amount with Qasim at the end of round 3 is 11.

Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
The only possible amount with Qasim at the end of round 8 can be 11 and therefore the amount at the end of round 8 with Ritesh will be 6. The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7. The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
If the amount with Suresh at the end of round 6 is 11 then the amount with Pulak at the end of round 6 will be 13 which is not possible. Therefore the amount with Suresh at the end of round 6 is 12 and the amount with Pulak at the end of round 6 is 12.

Q4: How many games were played with a bet of ₹2?
Ans: -6
Sol:
Its given that the table shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds, which means that in Pulak's column the numbers possible are 11 or 12 only, similarly in Qasim's column numbers possible are only 9 or 11 only, similarly in Ritesh's column numbers possible are 5,6,7,8 or 9 only and in Suresh's column numbers possible are 9,11 or 12 only.
Everyone started with 10 rupees and the total amount,i.e., 40 in each round remains the same. So we get the following table We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
As per the information given in the set the only possible amount with Qasim at the end of round 6 is 11. Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4. Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Qasim at the end of round 3 is either 9 or 11. If the amount is 9 then either amount with Ritesh has to be 10 or amount with Pulak has to to be 14, both of which is not possible. Therefore, amount with Qasim at the end of round 3 is 11.

Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
The only possible amount with Qasim at the end of round 8 can be 11 and therefore the amount at the end of round 8 with Ritesh will be 6. The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7. The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
If the amount with Suresh at the end of round 6 is 11 then the amount with Pulak at the end of round 6 will be 13 which is not possible. Therefore the amount with Suresh at the end of round 6 is 12 and the amount with Pulak at the end of round 6 is 12.
 The Games which had a bet of Rs.2 are as following
The Games which had a bet of Rs.2 are as following
Round 1 - Palak vs Qasim
Round 2 - Qasim vs Suresh
Round 3 - Palak vs Suresh
Round 4 - Ritesh vs Suresh
Round 5 - None
Round 6 - Palak vs Ritesh
Round 7 - None
Round 8 - Ritesh vs Suresh
Hence total number of games that were played with a bet of 2 is 6
Q5: Which of the following pairings was made in Round 5?
(a) Qasim and Suresh
(b) Pulak and Ritesh
(c) Pulak and Qasim
(d) Pulak and Suresh
Ans: (d)
Sol:
Its given that the table shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds, which means that in Pulak's column the numbers possible are 11 or 12 only, similarly in Qasim's column numbers possible are only 9 or 11 only, similarly in Ritesh's column numbers possible are 5,6,7,8 or 9 only and in Suresh's column numbers possible are 9,11 or 12 only.
Everyone started with 10 rupees and the total amount,i.e., 40 in each round remains the same. So we get the following table We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
We are given that at the end of 4th round both Pulak and Qasim had the same amount with them and that amount possible is only 11.
As per the information given in the set the only possible amount with Qasim at the end of round 6 is 11. Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4.
Amounts with Pulak and Qasim at the end of round 5 is decreased by 1 from the amounts which they had at the end of round 4, since the total amount will be same at the end of every round, so amounts with Ritesh and Suresh at the end of round 5 is increased by 1 from the amounts which they had at the end of round 4. Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Suresh at the end of round 2 is 8 and at the end of round 4 is 12, therefore, amount with Suresh at the end of round 3 is 10.
Amount with Qasim at the end of round 3 is either 9 or 11. If the amount is 9 then either amount with Ritesh has to be 10 or amount with Pulak has to to be 14, both of which is not possible. Therefore, amount with Qasim at the end of round 3 is 11.

Now Qasim has the same amount at the end of round 3 and round 4 so there must be another person whose amount is also same at the end of round 3 and round 4. This person can only be Pulak. So at the end of round 3 Pulak has 11 rupees and Ritesh has 8 rupees.
The only possible amount with Qasim at the end of round 8 can be 11 and therefore the amount at the end of round 8 with Ritesh will be 6. The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7.
The amount with Ritesh at the end of round 8 is 2 more than the amount with him at the end of round 7, so the amount with either Pulak or Suresh at the end of round 7 has to be 2 more than the amount at the end of round 8. This is only possible for Suresh who must have 12 rupees at the end of round 7 as Pulak cannot have rupees 15 at the end of round 7. The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
The amount with Qasim at the end of round 7 is 1 more than the amount with him at the end of round 6. So there must be another person whose amount at the end of round 7 is 1 less than the amount him at the end of round 6. This only possible person can be Ritesh. So amount with Ritesh at the end of round 6 will be 5.
If the amount with Suresh at the end of round 6 is 11 then the amount with Pulak at the end of round 6 will be 13 which is not possible. Therefore the amount with Suresh at the end of round 6 is 12 and the amount with Pulak at the end of round 6 is 12.

Direction: The following facts are known about the goals scored by these four players only. All the questions refer only to the goals scored by these four players.
The management of a university hockey team was evaluating performance of four women players - Amla, Bimla, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals.
- Only one goal was scored in every even numbered match.
- Harita scored more goals than Bimla.
- The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
- Bimla scored a goal in Match 1 and one each in three other consecutive matches.
- An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goals scored in either Match 1 or Match 5.
- The match in which the highest number of goals was scored was unique and it was not Match 5.
Q6: How many goals were scored in Match 7?
(a) 3
(b) 2
(c) 1
(d) Cannot be determined
Ans: (c)
Sol:
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:
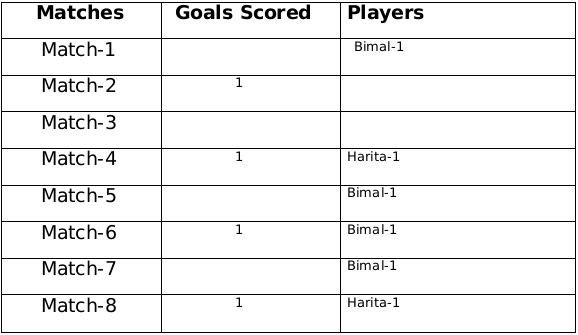
From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively. Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a=1, b=4 and c=2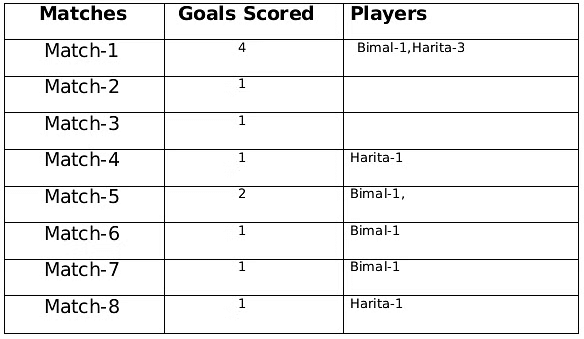 The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.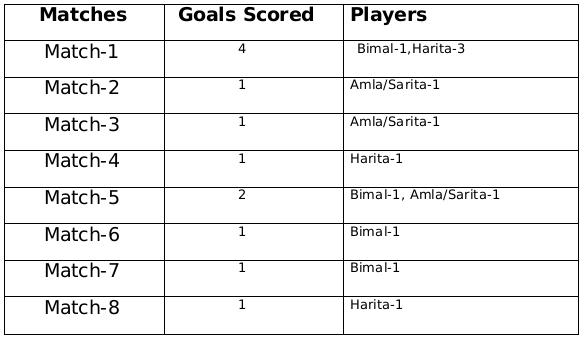
Q7: Which of the following is the correct sequence of goals scored in matches 1, 3, 5 and 7?
(a) 5, 1, 0, 1
(b) 3, 1, 2, 1
(c) 3, 2, 1, 2
(d) 4, 1, 2, 1
Ans: (d)
Sol:
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively. Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a=1, b=4 and c=2 The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
Q8: Which of the following statement(s) is/are true?
Statement-1: Amla and Sarita never scored goals in the same match.
Statement-2: Harita and Sarita never scored goals in the same match.
(a) Statement-1 only
(b) Statement-2 only
(c) Both the statements
(d) None of the statements
Ans: (c)
Sol:
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively. Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a=1, b=4 and c=2 The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
Q9: Which of the following statement(s) is/are false?
Statement-1: In every match at least one player scored a goal.
Statement-2: No two players scored goals in the same number of matches.
(a) Statement-1 only
(b) Both the statements
(c) Statement-2 only
(a) None of the statements
Ans: (b)
Sol:
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively. Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a=1, b=4 and c=2 The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
Q10: If Harita scored goals in one more match as compared to Sarita, which of the following statement(s) is/are necessarily true?
Statement-1: Amla scored goals in consecutive matches.
Statement-2: Sarita scored goals in consecutive matches.
(a) Statement-2 only
(b) None of the statements
(c) Statement-1 only
(d) Both the statements
Ans: (b)
Sol:
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively. Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a=1, b=4 and c=2 The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
|
77 videos|180 docs|96 tests
|
FAQs on Practice Questions: Games and Tournaments- 1 - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are games and tournaments? |  |
| 2. How are games and tournaments organized? |  |
| 3. What is the purpose of games and tournaments? |  |
| 4. How are winners determined in tournaments? |  |
| 5. What are the benefits of participating in games and tournaments? |  |
















