Practice Questions: Games and Tournaments- 2 | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
Direction for Question (1-4):
The game of Chango is a game where two people play against each other; one of them wins and the other loses, i.e., there are no drawn Chango games. 12 players participated in a Chango championship. They were divided into four groups: Group A consisted of Aruna, Azul, and Arif; Group B consisted of Brinda, Brij, and Biju; Group C consisted of Chitra, Chetan, and Chhavi; and Group D consisted of Dipen, Donna, and Deb.
Players within each group had a distinct rank going into the championship. The players have NOT been listed necessarily according to their ranks. In the group stage of the game, the second and third ranked players play against each other, and the winner of that game plays against the first ranked player of the group. The winner of this second game is considered as the winner of the group and enters a semi-final.
The winners from Groups A and B play against each other in one semi-final, while the winners from Groups C and D play against each other in the other semi-final. The winners of the two semi-finals play against each other in the final to decide the winner of the championship.
It is known that:
- Chitra did not win the championship.
- Aruna did not play against Arif. Brij did not play against Brinda.
- Aruna, Biju, Chitra, and Dipen played three games each, Azul and Chetan played two games each, and the remaining players played one game each.
Q1: Who won the championship?
(a) Chitra
(b) Aruna
(c) Brij
(d) Cannot be determined
Ans: (b)
Sol:
Group A:
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B:
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.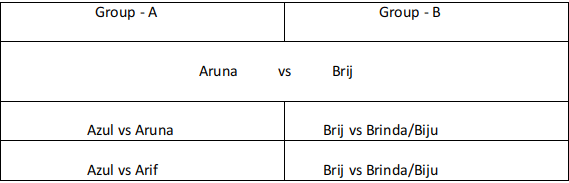
Group - C:
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.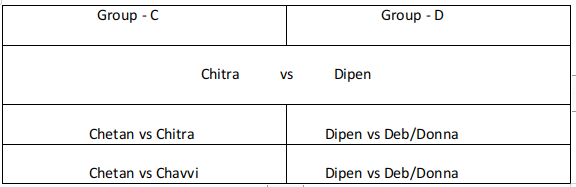
Aruna plays Chitra in the finals and wins the final round.
Aruna is the winner.
Q2: Who among the following was DEFINITELY NOT ranked first in his/her group?
(a) Dipen
(b) Aruna
(c) Brij
(d) Chitra
Ans: (a)
Sol:
Group A:
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B:
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.
Group - C:
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.
Aruna plays Chitra in the finals and wins the final round.
Dipen was ranked 2 or 3 in his group
Q3: Who among the following did NOT play against Chitra in the championship?
(a) Aruna
(b) Chetan
(c) Dipen
(d) Biju
Ans: (d)
Sol:
Group A:
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B:
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.
Group - C:
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round. Aruna plays Chitra in the finals and wins the final round.
Aruna plays Chitra in the finals and wins the final round.
Brij was the player from group B who played Chitra. Aruna played in finals, Chetan in round 2, and Dipen in semi finals
Q4: Which of the following pairs must have played against each other in the championship?
(a) Deb, Donna
(b) Azul, Biju
(c) Donna, Chetan
(d) Chitra, Dipen
Ans: (d)
Sol:
Group A:
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B:
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.
Group - C:
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.
Aruna plays Chitra in the finals and wins the final round.
Chitra and Dipen played in the semifinals
Direction for Question (5-10): 10 players - P1, P2, … , P10 - competed in an international javelin throw event. The number (after P) of a player reflects his rank at the beginning of the event, with rank 1 going to the topmost player. There were two phases in the event with the first phase consisting of rounds 1, 2, and 3, and the second phase consisting of rounds 4, 5, and 6. A throw is measured in terms of the distance it covers (in meters, up to one decimal point accuracy), only if the throw is a ‘valid’ one. For an invalid throw, the distance is taken as zero. A player’s score at the end of a round is the maximum distance of all his throws up to that round. Players are re-ranked after every round based on their current scores. In case of a tie in scores, the player with a prevailing higher rank retains the higher rank. This ranking determines the order in which the players go for their throws in the next round.
In each of the rounds in the first phase, the players throw in increasing order of their latest rank, i.e. the player ranked 1 at that point throws first, followed by the player ranked 2 at that point and so on. The top six players at the end of the first phase qualify for the second phase. In each of the rounds in the second phase, the players throw in decreasing order of their latest rank i.e. the player ranked 6 at that point throws first, followed by the player ranked 5 at that point and so on. The players ranked 1, 2, and 3 at the end of the sixth round receive gold, silver, and bronze medals respectively.
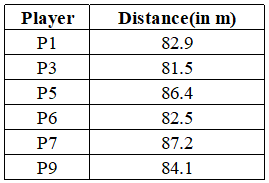
All the valid throws of the event were of distinct distances (as per stated measurement accuracy). The tables below show distances (in meters) covered by all valid throws in the first and the third round in the event.
Distances covered by all the valid throws in the first round
 Distances covered by all the valid throws in the third round
Distances covered by all the valid throws in the third round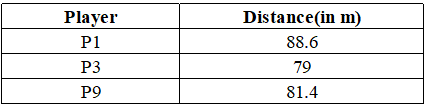 The following facts are also known.
The following facts are also known.
i. Among the throws in the second round, only the last two were valid. Both the throws enabled these players to qualify for the second phase, with one of them qualifying with the least score. None of these players won any medal.
ii. If a player throws first in a round AND he was also the last (among the players in the current round) to throw in the previous round, then the player is said to get a double. Two players got a double.
iii. In each round of the second phase, exactly one player improved his score. Each of these improvements was by the same amount.
iv. The gold and bronze medalists improved their scores in the fifth and the sixth rounds respectively. One medal winner improved his score in the fourth round.
v. The difference between the final scores of the gold medalist and the silver medalist, as well as the difference between the final scores of the silver medalist and the bronze medalist was 1.0 m.
Q5: Which two players got the double?
(a) P1, P8
(b) P2, P4
(c) P8, P10
(d) P1, P10
Ans: (c)
Sol:
Let us arrange the players in the order in which they throw in each round.
Round 1: Here the players throw in order of their initial seeds so the order is as follows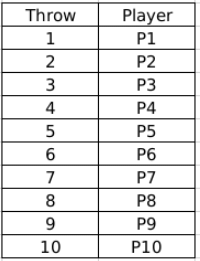 So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
Round 2: P2, P4, P8, P10 had the same relative rankings since they all have invalid throws, that is, 0 metres. Rest are arranged as per their throw distances.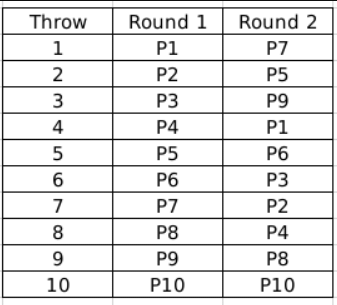 Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Round 3: In Round 3, we can see that P1 improved his score from 82.9 to 88.6. The other 2 participants did not improve their scores. Also after Round 3, P8 and P10 qualify, where one of P8 or P10 is at the sixth position. So at the end of Round 3, we can say that P6, P3, P2, and P4 are at the bottom 4 positions(ranks). One of P8 or P10 is at the sixth position. P1 > P7 > P5 > P9.
So at the end of round 3, the ranks are as follows: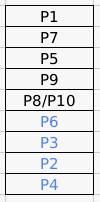 The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
Now let us consider the two players who got a double. Doubles happen in the transition between rounds.
1 -> 2 - Not possible
2 -> 3 - Possible if P10 reaches Rank 1 after round 2.
3 -> 4 - P8/P10 who is the last among qualifying will be the first to throw. So, here it definitely happens.
4 - > 5 AND 5 - > 6 not possible.
So, after Round 2, definitely, P10 reaches the top of the ranking. P8 is at the bottom. Hence, after Round 3, P10 either retains rank 1 or P1 surpasses him and P10 becomes Rank 2.
So, two combinations are possible at the end of Round 3: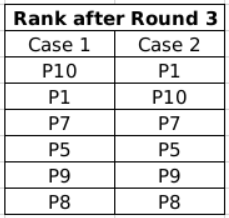 Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
P1 - 88.6 + x
P7 - 87.2 + x
P5 - 86.4 + x
P9 - 84.1 + x
The differences do not satisfy the condition. Hence, case 1 is invalidated.
Case 2: Here, P1 definitely wins a medal, and P10 does not. So, two of P7, P5 and P9 jumps above P10. Now, if we have three different people increasing their scores or distances in each of the three rounds, again we would not get a difference of 1 among the Gold, Silver and Bronze medallists. Hence, one of them increases his score twice and the other increases his score twice and none of them is P1.
Let us take the cases where P1 is individually the G, S and B medallists.
Case 1: P1 is a G medallist.
P1 - 88.6
The silver medallist is 87.6 and the bronze medallist is 86.6 metres. However, P10 has thrown for a distance that is greater than 87.2 metres. Hence, in this case, he would be the B medallist. Hence, this is not the right case.
Case 2: P1 is the S medallist.
P1 - 88.6
G - 89.6
B - 87.6
Now, if we see the differences
89.6 - 87.2 = 2.4
87.6 - 86.4 = 1.2
This satisfies the condition that P7 has increased his score twice to become the gold winner and P5 has increased it once to become the bronze winner.
Hence, P1 - Silver
P7 - Gold
P5 - Bronze
Hence, P8 and P10 got the doubles.
Q6: Which of the following can be the final score (in m) of P8?
(a) 81.9
(b) 0
(c) 82.7
(d) 85.1
Ans: (c)
Sol:
Let us arrange the players in the order in which they throw in each round.
Round 1: Here the players throw in order of their initial seeds so the order is as follows So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
Round 2: P2, P4, P8, P10 had the same relative rankings since they all have invalid throws, that is, 0 metres. Rest are arranged as per their throw distances. Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Round 3: In Round 3, we can see that P1 improved his score from 82.9 to 88.6. The other 2 participants did not improve their scores. Also after Round 3, P8 and P10 qualify, where one of P8 or P10 is at the sixth position. So at the end of Round 3, we can say that P6, P3, P2, and P4 are at the bottom 4 positions(ranks). One of P8 or P10 is at the sixth position. P1 > P7 > P5 > P9.
So at the end of round 3, the ranks are as follows: The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
Now let us consider the two players who got a double. Doubles happen in the transition between rounds.
1 -> 2 - Not possible
2 -> 3 - Possible if P10 reaches Rank 1 after round 2.
3 -> 4 - P8/P10 who is the last among qualifying will be the first to throw. So, here it definitely happens.
4 - > 5 AND 5 - > 6 not possible.
So, after Round 2, definitely, P10 reaches the top of the ranking. P8 is at the bottom. Hence, after Round 3, P10 either retains rank 1 or P1 surpasses him and P10 becomes Rank 2.
So, two combinations are possible at the end of Round 3: Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
P1 - 88.6 + x
P7 - 87.2 + x
P5 - 86.4 + x
P9 - 84.1 + x
The differences do not satisfy the condition. Hence, case 1 is invalidated.
Case 2: Here, P1 definitely wins a medal, and P10 does not. So, two of P7, P5 and P9 jumps above P10. Now, if we have three different people increasing their scores or distances in each of the three rounds, again we would not get a difference of 1 among the Gold, Silver and Bronze medallists. Hence, one of them increases his score twice and the other increases his score twice and none of them is P1.
Let us take the cases where P1 is individually the G, S and B medallists.
Case 1: P1 is a G medallist.
P1 - 88.6
The silver medallist is 87.6 and the bronze medallist is 86.6 metres. However, P10 has thrown for a distance that is greater than 87.2 metres. Hence, in this case, he would be the B medallist. Hence, this is not the right case.
Case 2: P1 is the S medallist.
P1 - 88.6
G - 89.6
B - 87.6
Now, if we see the differences
89.6 - 87.2 = 2.4
87.6 - 86.4 = 1.2
This satisfies the condition that P7 has increased his score twice to become the gold winner and P5 has increased it once to become the bronze winner.
Hence, P1 - Silver
P7 - Gold
P5 - Bronze
P8 comes between P9 and P6.
Hence, 82. 5 < P8 < 84.1
P8 = 82.7
Q7: Who threw the last javelin in the event?
(a) P7
(b) P1
(c) P9
(d) P10
Ans: (a)
Sol:
Let us arrange the players in the order in which they throw in each round.
Round 1: Here the players throw in order of their initial seeds so the order is as follows So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
Round 2: P2, P4, P8, P10 had the same relative rankings since they all have invalid throws, that is, 0 metres. Rest are arranged as per their throw distances. Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Round 3: In Round 3, we can see that P1 improved his score from 82.9 to 88.6. The other 2 participants did not improve their scores. Also after Round 3, P8 and P10 qualify, where one of P8 or P10 is at the sixth position. So at the end of Round 3, we can say that P6, P3, P2, and P4 are at the bottom 4 positions(ranks). One of P8 or P10 is at the sixth position. P1 > P7 > P5 > P9.
So at the end of round 3, the ranks are as follows: The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
Now let us consider the two players who got a double. Doubles happen in the transition between rounds.
1 -> 2 - Not possible
2 -> 3 - Possible if P10 reaches Rank 1 after round 2.
3 -> 4 - P8/P10 who is the last among qualifying will be the first to throw. So, here it definitely happens.
4 - > 5 AND 5 - > 6 not possible.
So, after Round 2, definitely, P10 reaches the top of the ranking. P8 is at the bottom. Hence, after Round 3, P10 either retains rank 1 or P1 surpasses him and P10 becomes Rank 2.
So, two combinations are possible at the end of Round 3: Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
P1 - 88.6 + x
P7 - 87.2 + x
P5 - 86.4 + x
P9 - 84.1 + x
The differences do not satisfy the condition. Hence, case 1 is invalidated.
Case 2: Here, P1 definitely wins a medal, and P10 does not. So, two of P7, P5 and P9 jumps above P10. Now, if we have three different people increasing their scores or distances in each of the three rounds, again we would not get a difference of 1 among the Gold, Silver and Bronze medallists. Hence, one of them increases his score twice and the other increases his score twice and none of them is P1.
Let us take the cases where P1 is individually the G, S and B medallists.
Case 1: P1 is a G medallist.
P1 - 88.6
The silver medallist is 87.6 and the bronze medallist is 86.6 metres. However, P10 has thrown for a distance that is greater than 87.2 metres. Hence, in this case, he would be the B medallist. Hence, this is not the right case.
Case 2: P1 is the S medallist.
P1 - 88.6
G - 89.6
B - 87.6
Now, if we see the differences
89.6 - 87.2 = 2.4
87.6 - 86.4 = 1.2
This satisfies the condition that P7 has increased his score twice to become the gold winner and P5 has increased it once to become the bronze winner.
Hence, P1 - Silver
P7 - Gold
P5 - Bronze
P7 the gold winner had already received rank 1 at the end of Round 5. Hence, he was the last one to throw in the tournament.
Q8: Who won the silver medal?
(a) P5
(b) P7
(c) P9
(d) P1
Ans: (c)
Sol:
Let us arrange the players in the order in which they throw in each round.
Round 1: Here the players throw in order of their initial seeds so the order is as follows So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
Round 2: P2, P4, P8, P10 had the same relative rankings since they all have invalid throws, that is, 0 metres. Rest are arranged as per their throw distances. Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Round 3: In Round 3, we can see that P1 improved his score from 82.9 to 88.6. The other 2 participants did not improve their scores. Also after Round 3, P8 and P10 qualify, where one of P8 or P10 is at the sixth position. So at the end of Round 3, we can say that P6, P3, P2, and P4 are at the bottom 4 positions(ranks). One of P8 or P10 is at the sixth position. P1 > P7 > P5 > P9.
So at the end of round 3, the ranks are as follows: The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
Now let us consider the two players who got a double. Doubles happen in the transition between rounds.
1 -> 2 - Not possible
2 -> 3 - Possible if P10 reaches Rank 1 after round 2.
3 -> 4 - P8/P10 who is the last among qualifying will be the first to throw. So, here it definitely happens.
4 - > 5 AND 5 - > 6 not possible.
So, after Round 2, definitely, P10 reaches the top of the ranking. P8 is at the bottom. Hence, after Round 3, P10 either retains rank 1 or P1 surpasses him and P10 becomes Rank 2.
So, two combinations are possible at the end of Round 3: Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
P1 - 88.6 + x
P7 - 87.2 + x
P5 - 86.4 + x
P9 - 84.1 + x
The differences do not satisfy the condition. Hence, case 1 is invalidated.
Case 2: Here, P1 definitely wins a medal, and P10 does not. So, two of P7, P5 and P9 jumps above P10. Now, if we have three different people increasing their scores or distances in each of the three rounds, again we would not get a difference of 1 among the Gold, Silver and Bronze medallists. Hence, one of them increases his score twice and the other increases his score twice and none of them is P1.
Let us take the cases where P1 is individually the G, S and B medallists.
Case 1: P1 is a G medallist.
P1 - 88.6
The silver medallist is 87.6 and the bronze medallist is 86.6 metres. However, P10 has thrown for a distance that is greater than 87.2 metres. Hence, in this case, he would be the B medallist. Hence, this is not the right case.
Case 2: P1 is the S medallist.
P1 - 88.6
G - 89.6
B - 87.6
Now, if we see the differences
89.6 - 87.2 = 2.4
87.6 - 86.4 = 1.2
This satisfies the condition that P7 has increased his score twice to become the gold winner and P5 has increased it once to become the bronze winner.
Hence, P1 - Silver
P7 - Gold
P5 - Bronze
Hence, P1 won the silver medal.
Q9: By how much did the gold medalist improve his score (in m) in the second phase?
(a) 1.0
(b) 2.0
(c) 2.4
(d) 1.2
Ans: (c) 2.4
Sol:
Let us arrange the players in the order in which they throw in each round.
Round 1: Here the players throw in order of their initial seeds so the order is as follows So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
Round 2: P2, P4, P8, P10 had the same relative rankings since they all have invalid throws, that is, 0 metres. Rest are arranged as per their throw distances. Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Round 3: In Round 3, we can see that P1 improved his score from 82.9 to 88.6. The other 2 participants did not improve their scores. Also after Round 3, P8 and P10 qualify, where one of P8 or P10 is at the sixth position. So at the end of Round 3, we can say that P6, P3, P2, and P4 are at the bottom 4 positions(ranks). One of P8 or P10 is at the sixth position. P1 > P7 > P5 > P9.
So at the end of round 3, the ranks are as follows: The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
Now let us consider the two players who got a double. Doubles happen in the transition between rounds.
1 -> 2 - Not possible
2 -> 3 - Possible if P10 reaches Rank 1 after round 2.
3 -> 4 - P8/P10 who is the last among qualifying will be the first to throw. So, here it definitely happens.
4 - > 5 AND 5 - > 6 not possible.
So, after Round 2, definitely, P10 reaches the top of the ranking. P8 is at the bottom. Hence, after Round 3, P10 either retains rank 1 or P1 surpasses him and P10 becomes Rank 2.
So, two combinations are possible at the end of Round 3: Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
P1 - 88.6 + x
P7 - 87.2 + x
P5 - 86.4 + x
P9 - 84.1 + x
The differences do not satisfy the condition. Hence, case 1 is invalidated.
Case 2: Here, P1 definitely wins a medal, and P10 does not. So, two of P7, P5 and P9 jumps above P10. Now, if we have three different people increasing their scores or distances in each of the three rounds, again we would not get a difference of 1 among the Gold, Silver and Bronze medallists. Hence, one of them increases his score twice and the other increases his score twice and none of them is P1.
Let us take the cases where P1 is individually the G, S and B medallists.
Case 1: P1 is a G medallist.
P1 - 88.6
The silver medallist is 87.6 and the bronze medallist is 86.6 metres. However, P10 has thrown for a distance that is greater than 87.2 metres. Hence, in this case, he would be the B medallist. Hence, this is not the right case.
Case 2: P1 is the S medallist.
P1 - 88.6
G - 89.6
B - 87.6
Now, if we see the differences
89.6 - 87.2 = 2.4
87.6 - 86.4 = 1.2
This satisfies the condition that P7 has increased his score twice to become the gold winner and P5 has increased it once to become the bronze winner.
Hence, P1 - Silver
P7 - Gold
P5 - Bronze
P7 improved by a total of 2.4.
Q10: What was the final score (in m) of the silver medalist?
(a) 89.6
(b) 88.4
(c) 88.6
(d) 87.2
Ans: (b)
Sol:
Let us arrange the players in the order in which they throw in each round.
Round 1: Here the players throw in order of their initial seeds so the order is as follows So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
Round 2: P2, P4, P8, P10 had the same relative rankings since they all have invalid throws, that is, 0 metres. Rest are arranged as per their throw distances. Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Round 3: In Round 3, we can see that P1 improved his score from 82.9 to 88.6. The other 2 participants did not improve their scores. Also after Round 3, P8 and P10 qualify, where one of P8 or P10 is at the sixth position. So at the end of Round 3, we can say that P6, P3, P2, and P4 are at the bottom 4 positions(ranks). One of P8 or P10 is at the sixth position. P1 > P7 > P5 > P9.
So at the end of round 3, the ranks are as follows: The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
Now let us consider the two players who got a double. Doubles happen in the transition between rounds.
1 -> 2 - Not possible
2 -> 3 - Possible if P10 reaches Rank 1 after round 2.
3 -> 4 - P8/P10 who is the last among qualifying will be the first to throw. So, here it definitely happens.
4 - > 5 AND 5 - > 6 not possible.
So, after Round 2, definitely, P10 reaches the top of the ranking. P8 is at the bottom. Hence, after Round 3, P10 either retains rank 1 or P1 surpasses him and P10 becomes Rank 2.
So, two combinations are possible at the end of Round 3: Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions' distances are in AP.
P1 - 88.6 + x
P7 - 87.2 + x
P5 - 86.4 + x
P9 - 84.1 + x
The differences do not satisfy the condition. Hence, case 1 is invalidated.
Case 2: Here, P1 definitely wins a medal, and P10 does not. So, two of P7, P5 and P9 jumps above P10. Now, if we have three different people increasing their scores or distances in each of the three rounds, again we would not get a difference of 1 among the Gold, Silver and Bronze medallists. Hence, one of them increases his score twice and the other increases his score twice and none of them is P1.
Let us take the cases where P1 is individually the G, S and B medallists.
Case 1: P1 is a G medallist.
P1 - 88.6
The silver medallist is 87.6 and the bronze medallist is 86.6 metres. However, P10 has thrown for a distance that is greater than 87.2 metres. Hence, in this case, he would be the B medallist. Hence, this is not the right case.
Case 2: P1 is the S medallist.
P1 - 88.6
G - 89.6
B - 87.6
Now, if we see the differences
89.6 - 87.2 = 2.4
87.6 - 86.4 = 1.2
This satisfies the condition that P7 has increased his score twice to become the gold winner and P5 has increased it once to become the bronze winner.
Hence, P1 - Silver
P7 - Gold
P5 - Bronze
P1 - 88.6 m.
|
77 videos|180 docs|96 tests
|
FAQs on Practice Questions: Games and Tournaments- 2 - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What is the importance of practice in games and tournaments? |  |
| 2. How can practice sessions be structured for games and tournaments? |  |
| 3. What strategies can be used to enhance performance in games and tournaments? |  |
| 4. How can players overcome nervousness and anxiety during games and tournaments? |  |
| 5. What are some common challenges faced by players in games and tournaments? |  |





















