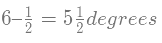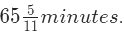Important Formulas: Clock and Calendar | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
| Table of contents |

|
| Clock |

|
| Calendar |

|
| Important Observations and Formulas of Clock |

|
| Important Observations and Formulas for Calendars |

|
| Sample Clock and Calendar Questions with Solution |

|
The number of questions related to the clock and calendar topic in competitive exams can vary greatly depending on the specific exam and its structure. Generally, these topics may constitute a small portion of the reasoning or quantitative section, with possibly 1-5 questions in a standard set, though this is not fixed and can change with each exam's format.
Clock
- Minute Spaces: The clock face or dial is a circular surface divided into 60 equal parts, known as minute spaces.
- Hour Hand and Minute Hand: The smaller hand on a clock is known as the hour hand or shorthand, while the larger hand (instead of one) is referred to as the minute hand or long hand.

Calendar
Ordinary & Leap Year
Ordinary Year: An ordinary year, which is not a leap year, consists of 365 days.
Leap Year: A leap year comprises 366 days, and it follows two conditions:
(a) Every year divisible by 4 is a leap year, except for centuries.
(b) Every 4th century is a leap year, while other centuries are not considered leap years.
Odd Days
When determining the day of the week for a given date, we employ the concept of 'odd days.' In a given timeframe, the days beyond complete weeks are referred to as odd days.

Important Observations and Formulas of Clock
- A clock is a complete circle having 360 degrees. It is divided into 12 equal parts i.e. each part:
360/12 = 30 - As the minute hand takes a complete round in one hour it covers 360 degrees in 60 min.

- Also, as the hour hand covers just one part out of the given 12 parts in one hour, this implies
Hour Hand covers 300 in 60 min. i.e. 1/2 degree per minute. - Therefore, the relative speed of the minute hand is

- Every hour, both the hands coincide once. In 12 hours, they will coincide 11 times.
It happens due to only one such incident between 12 and 1’o clock. - The hands are in the same straight line when they are coincident or opposite to each other.
- When the two hands are at a right angle, they are 15-minute spaces apart.
- In one hour, they will form two right angles and in 12 hours there are only 22 right angles. It happens due to right angles formed by the minute and hour hand at 3’o clock and 9’o clock.
- When the hands are in opposite directions, they are 30-minute spaces apart.
- If a clock indicates 9.15, when the correct time is 9, it is said to be 15 minutes too fast. On the other hand, if it indicates 8.45, when the correct time is 9, it is said to be 15 minutes too slow.
- If both the hour hand and minute hand move at their normal speeds, then both the hands meet after 65511

- 22 times in a day, the hands of a clock will be in a straight line but opposite in direction.
- 44 times in a day, the hands of a clock will be straight.
- 44 times in a day, the hands of a clock are at right angles.
- 22 times in a day, the hands of a clock coincide.
Clocks Formula 1:
If the minute hand lags behind the hour hand, the angle between the two hands at M minutes past H o'clock can be calculated using the following formula: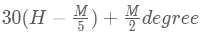
Clocks Formula 2:
If the minute hand is ahead of the hour hand, the angle between the two hands at M minutes past H o'clock can be determined using the following formula: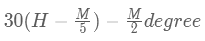
Important Observations and Formulas for Calendars
- A leap year has 366 days
- Every year divisible by 4 is a leap year, if it is not a century.
- Every 4th century is a leap year and no other century is a leap year.
- Counting odd days
1 ordinary year ≡ 365 days ≡ (52 weeks + 1 day)
Hence number of odd days in 1 ordinary year= 1.
1 leap year = 366 days = (52 weeks + 2 days)
Hence number of odd days in 1 leap year= 2.
100 years = (76 ordinary years + 24 leap years)
= (76 x 1 + 24 x 2) odd days
= 124 odd days.
= (17 weeks + 5 days)
= 5 odd days.
Hence number of odd days in 100 years = 5.
Number of odd days in 200 years = (5 x 2) = 10 = 3 odd days
Sample Clock and Calendar Questions with Solution
Q1: If your birthday falls on the third Monday of September 2023, on what date will your birthday fall in 2027?
Sol:
In 2023, September 1st is a Friday
The third Monday of September falls on the day after 14 days (2 weeks)
In 2027, September 1st will be a Wednesday (since the days advance by 2 days each year)
Adding 14 days (2 weeks) to Wednesday, we get Wednesday + 14 = Thursday
So, your birthday in 2027 will fall on a Thursday
Q2: Sarah set her clock to show 3 o’clock in the afternoon. How many degrees will the hour hand of the clock rotate when the clock shows 8 o’clock at night?
Sol:
From 3 o’clock in the afternoon to 8 o’clock at night is a total of 5 hours.
Since standard clock, the hour hand completes 360°- in 12 hours.
So in 1 hour, it moves 360° / 12 hours = 30° per hour.
Now, for 5 hours:
Degrees rotated by the hour hand = 5 hours × 30° per hour = 150°
So, the hour hand will rotate 150° from 3 o’clock in the afternoon to 8 o’clock at night.
Q3: Determine the year in which the calendar will repeat exactly as it was in the year 2015.
Sol:
2015 is a non-leap year.
To find a year with the same calendar, we need to look for a year that is 11 years after 2015
2015 + 11 = 2026
Therefore, the calendar for the year 2026 will be the same as the calendar for the year 2015
Q4: Thomas Miller, a curious individual, approaches his mathematics teacher with a question regarding the day on which the 1st of the month will occur, given that the 9th of the month falls on the day just before Sunday.
Sol:
When the 9th of the month falls on the day preceding Sunday, we establish that the 8th of the month is a Saturday.
To determine the day when the 1st of the same month will arrive, we proceed with the following sequence:
- Saturday (8th)
- Sunday (9th)
- Monday (10th)
- Tuesday (11th)
- Wednesday (12th)
- Thursday (13th)
- Friday (14th)
Therefore, if the 9th of the month is positioned just before Sunday, the 1st of the same month will fall on a Friday.
Q5: A wager was made between two friends, Harry and Ronald, to determine the probability of randomly selecting a leap year that has 53 Fridays.
Sol:
2/7 in a leap year there are 366 days means 52 weeks and 2days. So already we have 52 Fridays.
Now the rest two days can be:
- (Sunday, Monday)
- (Monday, Tuesday)
- (Tuesday, Wed)
- (Wednesday, Thursdays)
- (Thursday, Friday)
- (Friday, Sat)
- (Sat, Sun)
So, the probability of 53 Fridays = 2/7
|
1365 videos|1312 docs|1010 tests
|
|
1365 videos|1312 docs|1010 tests
|

|
Explore Courses for SSC CGL exam
|

|