Important Formulas: Permutations and Combinations | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
Permutation and Combination Formulas
- Number of all permutations of n things, taken r at a time, is given by

- Number of all combinations of n things, taken r at a time, is given by


Points to Remember
- Factorial of any negative quantity is not valid.
- If a particular thing can be done in m ways and another thing can be done in n ways, then
- Either one of the two can be done in m + n ways and
- Both of them can be done in m × n ways
- 0! = 1
- 1! = 1
- If from the total set of n objects and ‘p1’ are of one kind and ‘p2’ and ‘p3’ and so on …. till pr are others respectively then

- nPn = n!
- ncn = 1
- nc0 = 1
- ncr = nc(n-r)
- nc0+nc1+nc2+nc3+…ncn = 2n
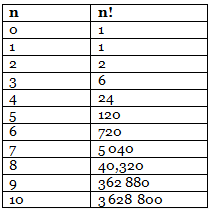
Permutation and Combination Formulas- Factorial
n ! = n(n-1)(n-2) …… 1 Eg. – 5! = 5(5-1)(5-2)(5-3)(5-4) = 5(4)(3)(2)(1)
Standard Truths
- 0! = 1
- n! only exists of n >= 0 and doesn’t exist for n < 0

Permutations Formulas
Number of ways in which Permutations out of n things r things can be SELECTED & ARRANGED (denoted by nPr).
nPr = number of permutations (arrangements) of n things taken r at a time.
Eg.
- Arrangement of Letters/Alphabets to form words with meaning or without meaning.
- Arrangements of balls on a table.
Formulas for Combinations
The number of ways in which r things at a time can be SELECTED from from n things is Combinations (represented by nCr).. nCr = Number of combinations (selections) of n things taken r at a time.
 ; where n ≥ r (n is greater than or equal to r).
; where n ≥ r (n is greater than or equal to r).
Eg.
- Selections for people from total numbers who want to go out on a picnic.
- Filling posts with people
- Selection for a sports team out of available players
- Selection of balls from a bag
Important Properties
Property 1
Number of permutations (or arrangements) of n different things taken all at a time = n!
Property 2
For Objects in which P1 are alike and are of one type, P2 are alike or other different type and P3 are alike or another different type and the rest must be all different, Number of permutations =
Property 3
When repetition is allowed number of permutations of n different things taken r at a time = n × n× n ×… (r times) = nr
Property 4
Here, we are counting the number of ways in which k balls can be distributed into n boxes under various conditions. The conditions which are generally asked are
- The balls are either distinct or identical.
- No box can contain more than one ball or any box may contain more than one ball.
- No box can be empty or any box can be empty.

Other Properties
- nPr = r! × nCr
- nCr + nCr-1 = n+1Cr
- nCx = nCy when x = y or x + y = n
- nCr = nPn-r
- r . nCr = n n-1Cr-1
- For nCr to be greatest
(a) if n is even, r = n/2
(b) if n is odd,
|
1365 videos|1312 docs|1010 tests
|
|
1365 videos|1312 docs|1010 tests
|

|
Explore Courses for SSC CGL exam
|

|



 ; where n ≥ r (n is greater than or equal to r).
; where n ≥ r (n is greater than or equal to r).

















