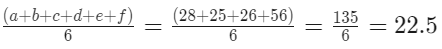Practice Questions: Number System | Quantitative Aptitude (Quant) - CAT PDF Download

This provides a focused set of practice questions on the Number System, designed to strengthen conceptual clarity and problem-solving skills. It includes both Multiple Choice Questions (MCQs) and Type in the Answer (TITA) formats, helping aspirants prepare effectively for competitive exams that test numerical aptitude.

MCQ Format Questions

Q1: Consider six distinct natural numbers such that the average of the two smallest numbers is 14, and the average of the two largest numbers is 28. Then, the maximum possible value of the average of these six numbers is
(a) 23
(b) 24
(c) 23.5
(d) 22.5

Ans: (d)
Sol: Let the six numbers be a, b, c, d, e, f in ascending order
(a + b)/2 = 14
(a + b) = 28
(e + f)/2 =  28
(e + f) = 56
If we want to maximise the average then we have to maximise the value of c and d and maximise e and minimise f
e + f = 56
As e and f are distinct natural numbers so possible values are 27 and 29
Therefore c and d will be 25 and 26 respecitively

Q2: For some natural number n, assume that (15,000)! is divisible by (n!)!. The largest possible value of n is
(a) 4
(b) 7
(c) 6
(d) 5

Ans: (b)
Sol: To find the largest possible value of n, we need to find the value of n such that n! is less than 15000.
7! = 5040
8! = 40320 > 15000
This implies 15000! is not divisible by 40320!
Therefore, maximum value n can take is 7.
The answer is option B.

Q3: A school has less than 5000 students and if the students are divided equally into teams of either 9 or 10 or 12 or 25 each, exactly 4 are always left out. However, if they are divided into teams of 11 each, no one is left out. The maximum number of teams of 12 each that can be formed out of the students in the school is

Sol: Since the total number of students, when divided by either 9 or 10 or 12 or 25 each, gives a remainder of 4, the number will be in the form of LCM(9,10,12,25)k + 4 = 900k + 4.
It is given that the value of 900k + 4 is less than 5000.
Also, it is given that 900k + 4 is divided by 11.
It is only possible when k = 2 and total students = 1804.
So, the number of 12 students group = 1800/12 = 150.

Q4: For a 4-digit number, the sum of its digits in the thousands, hundreds and tens places is 14, the sum of its digits in the hundreds, tens and units places is 15, and the tens place digit is 4 more than the units place digit. Then the highest possible 4-digit number satisfying the above conditions is

Sol: Given the 4 digit number:
Considering the number in thousands digit is a number in the hundredth digit is b, number in tens digit is c, number in the units digit is d.
Let the number be abcd.
Given that a+b+c = 14. (1)
b+c+d = 15. (2)
c = d+4. (3).
In order to find the maximum number which satisfies the condition, we need to have abcd such that a is maximum which is the digit in thousands place in order to maximize the value of the number. b, c, and d are less than 9 each as they are single-digit numbers.
Substituting (3) in (2) we have b + d + 4 + d = 15, b+2*d = 11.  (4)
Subtracting (2) and (1) : (2) - (1) = d = a + 1.   (5)
Since c cannot be greater than 9 considering c to be the maximum value 9 the value of d is 5.
If d = 5, using d = a + 1, a = 4.
Hence the maximum value of a = 4 when c = 9, d = 5.
Substituting b + 2*d = 11. b = 1.
The highest four-digit number satisfying the condition is 4195

Q5: How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7?

Sol: Let the number be 'abc'. Then, 2 < a × b × c < 7. The product can be 3, 4, 5, 6.
Thus a total of 12 + 3 + 6 = 21 such numbers can be formed.

Q6: How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3?

Sol: According to the question;
The 4 digit number having 7 before 3 can be formed

Case I: When 7 is thousand placed, then 3 may be hundred place, tens place and unit place
From the following 73xy, 7x3y, 7xy3 are formed
Total such number formed = 3 × (8 × 7) = 168

Case II: When 7 is hundred placed, then 3 may be tens place and unit place
From the following x73y, x7y3 are formed
Total such number formed = 2 × (7 × 7) = 98

Case III: When 7 is tens place and 3 is unit place
From the following xy73 is formed
Total such number formed = 7 × 7 = 49

The total such number formed = 168 + 98 + 49 = 315

∴ The 4 digit number greater than 1000 with 7 before 3 is 315.

Q7: How many integers in the set {100, 101, 102, ..., 999} have at least one digit repeated?

Sol: The total numbers of integers are
⇒ 999 - 100 + 1 = 900

Let N be the number of integers with no repeated digits
Total 10 digits we have (0, 1, ..., 9)
The first digit can't be 0, we have 9 digits
For the second digit, we have 9 digits
For the third digit, we have 8 digits

Total number of digits with no repetition
⇒ N = 9 × 9 × 8 = 648

Integers with at least one digit repeated
⇒ 900 - N
⇒ 900 - 648 = 252

Q8: In a six-digit number, the sixth, that is, the rightmost, digit is the sum of the first three digits, the fifth digit is the sum of first two digits, the third digit is equal to the first digit, the second digit is twice the first digit and the fourth digit is the sum of fifth and sixth digits. Then, the largest possible value of the fourth digit is

Sol: Let the first digit be 'a'
Now according to the question,
Third digit = The first digit⇒ a
The second digit = 2 × The first digit
⇒ 2 × a
⇒ 2a
The sixth digit = The sum of (first digit + second digit + third digit)
⇒ a + 2a + a
⇒ 4a
The fifth digit = The sum of first two digit
⇒ a + 2a
⇒ 3a
The fourth digit = The sum of (fifth digit + sixth digit)
⇒ 3a + 4a
⇒ 7a
So we can see our fourth digit should be a multiple of 7
And we can say that the largest possible value of the fourth digit will be 7 when the value of 'a' will be 1
Because if we put 'a' equal to 2 it will give the two-digit number equal to (7 × 2 = 14) for the fourth digit which is not possible.
∴ The largest possible value of the fourth digit is only 7.

Q9: Of 128 boxes of oranges, each box contains at least 120 and at most 144 oranges. X is the maximum number of boxes containing the same number of oranges. What is the minimum value of X?
(a) 5 
(b) 103 
(c) 6 
(d) Cannot be determined

Ans: (c)
Sol: Each box contains at least 120 and at most 144 oranges.
So boxes may contain 25 different numbers of oranges among 120, 121, 122, .... 144.
Lets start counting.
1st 25 boxes contain different numbers of oranges and this is repeated till 5 sets as 25*5=125.
Now we have accounted for 125 boxes. Still 3 boxes are remaining. These 3 boxes can have any number of oranges from 120 to 144.
Already every number is in 5 boxes. Even if these 3 boxes have different number of oranges, some number of oranges will be in 6 boxes.
Hence the number of boxes containing the same number of oranges is at least 6.

Q10: Anita had to do a multiplication. Instead of taking 35 as one of the multipliers, she took 53. As a result, the product went up by 540. What is the new product?
(a) 1050
(b) 540
(c) 1440
(d) 1590

Ans: (a)
Sol: Let the number be X.
From the given information, 53x - 35x = 540 => 18x = 540 => x = 30
So, new product = 35*30 = 1050

Q11: Convert the number 1982 from base 10 to base 12. The result is:
(a) 1182
(b) 1912
(c) 1192
(d) 1292

Ans: (c)
Sol: Quotient of 1982/12 = 165, remainder = 2
Quotient of 165/12 = 13, remainder = 9
Quotient of 13/12 = 1, remainder = 1
Remainder of 1/12 = 1
So, the required number in base 12 = 1192

Q12: A is the set of positive integers such that when divided by 2, 3, 4, 5, 6 leaves the remainders 1, 2, 3, 4, 5 respectively. How many integers between 0 and 100 belong to set A?
(a) 81
(b) 59
(c) 28
(d) None of these

Ans: (b)
Sol: Let the number 'n' belong to the set A.
Hence, the remainder when n is divided by 2 is 1
The remainder when n is divided by 3 is 2
The remainder when n is divided by 4 is 3
The remainder when n is divided by 5 is 4 and
The remainder when n is divided by 6 is 5
So, when (n+1) is divisible by 2,3,4,5 and 6.
Hence, (n+1) is of the form 60k for some natural number k.
And n is of the form 60k^-1
Between numbers 0 and 100, only 59 is of the form above.

Q13: How many five-digit numbers can be formed using the digits 2, 3, 8, 7, 5 exactly once such that the number is divisible by 125?
(a) 0
(b) 1
(c) 4
(d) 3

Ans: (c)
Sol: As we know for a number to be divisible by 125, its last three digits should be divisible by 125
So for a five digit number, with digits 2,3,8,7,5 its last three digits should be 875 and 375
Hence only 4 numbers are possible with its three digits as 875 and 375
I.e. 23875, 32875, 28375, 82375

Q14: A student instead of finding the value of 7/8 of a number, found the value of 7/18 of the number. If his answer differed from the actual one by 770, find the number.
(a) 1584
(b) 2520
(c) 1728
(d) 1656

Ans: (a)
Sol: let's say number is x.
So, 7x/8 - 7x/18 = 770
or x = 1584

Q15: P and Q are two positive integers such that PQ = 64. Which of the following cannot be the value of P + Q?
(a) 20
(b) 65
(c) 16
(d) 35

Ans: (d)
Sol: When PQ = 64
Possible values of P and Q are as follows:
64 x 1 ; 32 x 2 ; 16x4 ; 8 x 8
So possible sums are 65,34,20 and 16
Hence answer would be (d)

Q16: If a number 774958A96B is to be divisible by 8 and 9, the respective values of A and B will be
(a) 7 and 8
(b) 8 and 0
(c) 5 and 8
(d) None of these

Ans: (b)
Sol: According to the divisible rule of 9, the sum of all digits should be divisible by 9.
i.e. 55+A+B = 9k
So sum can be either 63 or 72.
For 63, A+B should be 8.
In given options, option B has values of A and B whose sum is 8 and by putting them we are having a number which divisible by both 9 and 8.
Hence answer will be B.

Q17: Three times the first of three consecutive odd integers is 3 more than twice the third. What is the third integer? 
(a) 15 
(b) 9 
(c) 11 
(d) 5

Ans: (a)
Sol: Suppose consecutive odd integers are: (a-2), a, (a+2)
Hence, 3a-6 = 2(a+2) + 3 => a=13
a+2 = 15

Q18: The sum of two integers is 10 and the sum of their reciprocals is 5/12. Then the larger of these integers is
(a) 2
(b) 4
(c) 6
(d) 8

Ans: (c)
Sol: let's say integers are x and y
so x + y = 10 ⇒ y = 10 - x
and 1/x + 1/y = 5/12
1/x + 1/10-x = 5/12
⇒ (10 - x + x)*12 = 5*x(10-x)
⇒ 120 = 50x - 5x²
⇒ 24 = 10x - x²
⇒ x = 4, 6
⇒ y = 6 or 4
The bigger of the two numbers is 6.

Q19: In Sivakasi, each boy's quota of match sticks to fill into boxes is not more than 200 per session. If he reduces the number of sticks per box by 25, he can fill 3 more boxes with the total number of sticks assigned to him. Which of the following is the possible number of sticks assigned to each boy?
(a) 200
(b) 150
(c) 125
(d) 175

Ans: (b)
Sol: Let the number of sticks assigned to each boy be N.
Let the number of boxes be M.
So, number of sticks per box = N/M
Now, if he reduces the number of sticks in each box, the equation becomes N/(M+3) = N/M - 25
So, 25 = N/M - N/(M+3)
From the options, if N = 150, then, we get 25 = 150 [ 1/M - 1/(M+3) ]
=> 1/6 = 1/M - 1/(M+3) => M = 3
So, the number of sticks assigned to each boy = 150

Q20: If 8 + 12 = 2, 7 + 14 = 3 then 10 + 18 = ? 
(a) 10 
(b) 4 
(c) 6 
(d) 18

Ans: (a)
Sol: 8+12 =( 20 = 2+0) = 2
7 + 14 =( 21 = 2+1) = 3
10 + 18= (28= 2+8) = 10

​TITA Format Questions

Q1: How many factors of 2 raised to the power 4 multiplied by 5 raised to the power 3 multiplied by 7 raised to the power 4 are odd numbers?

Ans: 

Given number:

2^4 × 5^3 × 7^4

To find how many odd factors this number has, we need to remove all powers of 2, because any factor containing 2 will be even.

So we are left with:

5^3 × 7^4

Now, to find the total number of factors of this part, we use the formula for counting factors:

For a number in the form a^m × b^n, the total number of factors is (m + 1) × (n + 1)

Here:

Exponent of 5 is 3 → (3 + 1) = 4

Exponent of 7 is 4 → (4 + 1) = 5

Multiply them: 4 × 5 = 20

Final Answer: 20

Q2: If a three-digit number ‘abc’ has 2 factors (where a, b, c are digits), how many factors does the 6-digit number ‘abcabc’ have?

Ans: 

We are given:

A 3-digit number 'abc' has exactly 2 factors.

We are to find how many factors the 6-digit number 'abcabc' has.

Step 1: Understand What It Means for a Number to Have Exactly 2 Factors

A number has exactly 2 positive factors only if it is a prime number.

So, 'abc' is a 3-digit prime number. Let's call this number N.

So:

N = abc

N is a prime number between 100 and 999

Hence, N has exactly 2 factors: 1 and itself

Step 2: Understand the Structure of the Number 'abcabc'

The number 'abcabc' can be written as:

abcabc = 1000 x abc + abc = abc(1000 + 1) = 1001 x abc

So: abcabc = 1001 x N

Step 3: Prime Factorisation of 1001

1001 = 7 x 11 x 13

So: abcabc = 1001 x N = 7 x 11 x 13 x N

Since N is a 3-digit prime number, and not equal to 7, 11, or 13 (as those are all less than 100), we now know that abcabc has 4 distinct prime factors:

7, 11, 13, and N

So the prime factorisation of abcabc is:

7^1 x 11^1 x 13^1 x N^1

Step 4: Use Formula to Find Total Number of Factors

To find the total number of positive factors of a number, use the formula:

If a number has prime factorisation:

p1^a1 x p2^a2 x ... x pk^ak

Then the total number of factors is:

(a1 + 1)(a2 + 1)...(ak + 1)

Here:

All exponents are 1

There are 4 prime factors

So:

Number of factors = (1+1)(1+1)(1+1)(1+1) = 2 x 2 x 2 x 2 = 16

Final Answer: 16

Q3: How many of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7?

Ans: 

Step 1: Total numbers

We are considering all integers from 1 to 120 → total = 120 numbers

We want to count how many of these are not divisible by 2, 5, or 7

This is a classic inclusion-exclusion problem.

Let’s define:

A = numbers divisible by 2

B = numbers divisible by 5

C = numbers divisible by 7

We will compute how many numbers are divisible by 2, 5, or 7, and subtract that from 120.

Step 2: Count multiples from 1 to 120

Numbers divisible by 2 → floor(120 / 2) = 60

Numbers divisible by 5 → floor(120 / 5) = 24

Numbers divisible by 7 → floor(120 / 7) = 17

Now count overlaps:

Divisible by both 2 and 5 (i.e. by 10) → floor(120 / 10) = 12

Divisible by both 2 and 7 (i.e. by 14) → floor(120 / 14) = 8

Divisible by both 5 and 7 (i.e. by 35) → floor(120 / 35) = 3

Divisible by 2, 5, and 7 (i.e. by 70) → floor(120 / 70) = 1

Step 3: Apply the inclusion-exclusion principle

Total numbers divisible by 2, 5, or 7 =

60 + 24 + 17 – 12 – 8 – 3 + 1

= 101 – 23 + 1

= 79

Step 4: Subtract from the total

Numbers not divisible by 2, 5, or 7 =

120 – 79 = 41

Final Answer: 41

Q4: If N and x are positive integers such that Nⁿ = 2¹⁶⁰ and N² + 2ⁿ is an integral multiple of 2ˣ, then the largest possible x is …

Ans:

We are given:

N raised to power N = 2 raised to power 160

N squared + 2 raised to power N is divisible by 2 raised to power x

N and x are positive integers

We are to find the largest possible value of x .

Step 1: Use the equation N^N = 2^160

This tells us that N must be a power of 2, since only powers of 2 raised to themselves can result in another power of 2.

Let’s assume:

N = 2^k

Then:

N^N = (2^k)^(2^k) = 2^(k * 2^k)

Set this equal to 2^160:

k * 2^k = 160

Try small values of k:

k = 1 → 1 * 2 = 2

k = 2 → 2 * 4 = 8

k = 3 → 3 * 8 = 24

k = 4 → 4 * 16 = 64

k = 5 → 5 * 32 = 160

So:

k = 5 → N = 2^5 = 32

Step 2: Plug into second condition

We are told: N^2 + 2^N is divisible by 2^x

Now we know:

N = 32

So N^2 = 32^2 = 1024

2^N = 2^32

So:

Expression = 1024 + 2^32

We want to find the highest power of 2 that divides this sum.

Let’s write both terms as powers of 2:

1024 = 2^10

2^32 = 2^32

So:

Expression = 2^10 + 2^32

Factor out the smaller power:

= 2^10 × (1 + 2^22)

Now analyse:

The term (1 + 2^22) is an odd number because it's 1 plus a large even number.

Therefore, the entire expression has exactly 10 factors of 2.

Final Answer: 10

Q5: N = (18n² + 9n + 8)/n; where N belongs to integer. How many integral solutions of N are possible?

Ans:

We are given:

N = (18n² + 9n + 8) / n, where N is an integer.

We are to find how many integral values of N are possible.

Step 1: Simplify the expression

Given:

N = (18n² + 9n + 8) / n

Split the numerator:

N = (18n²)/n + (9n)/n + 8/n

N = 18n + 9 + 8/n

So:

N = 18n + 9 + 8/n

We want N to be an integer.

This means that 8/n must be an integer, which implies that n must divide 8.

Step 2: Find all integer divisors of 8

The integer divisors of 8 are:

±1, ±2, ±4, ±8

That gives us 8 possible values for n .

Let’s compute N for each value of n:

Case 1: n = 1

N = 18(1) + 9 + 8/1 = 18 + 9 + 8 = 35

Case 2: n = -1

N = 18(-1) + 9 + 8/(-1) = -18 + 9 - 8 = -17

Case 3: n = 2

N = 18(2) + 9 + 8/2 = 36 + 9 + 4 = 49

Case 4: n = -2

N = 18(-2) + 9 + 8/(-2) = -36 + 9 - 4 = -31

Case 5: n = 4

N = 18(4) + 9 + 8/4 = 72 + 9 + 2 = 83

Case 6: n = -4

N = 18(-4) + 9 + 8/(-4) = -72 + 9 - 2 = -65

Case 7: n = 8

N = 18(8) + 9 + 8/8 = 144 + 9 + 1 = 154

Case 8: n = -8

N = 18(-8) + 9 + 8/(-8) = -144 + 9 - 1 = -136

Step 3: Count the distinct integral values of N

From above, the values of N are:

35, -17, 49, -31, 83, -65, 154, -136

All 8 values are distinct integers.

Final Answer: 8 integral solutions for N are possible.