Important Formula: Geometry | Quantitative Aptitude for SSC CGL PDF Download
Definition
Geometry revolves around shapes and their characteristics. It can be categorized into two main branches: Plane Geometry, which deals with flat shapes like lines, circles, and triangles—shapes drawable on a piece of paper; and Solid Geometry, which pertains to the geometry of three-dimensional space, the type of space we inhabit.
Perimeter
To elaborate, perimeter refers to the boundary that encloses or surrounds a two-dimensional shape.
Basic Geometry Formulas-Area, Volume and Perimeter
Largest Possible Sphere
In this type you will be given a cube of “a” cm and will be asked the volume of largest possible sphere which can be chiseled out from it.
Diagonal of the Sphere: a/2 = Radius
Remaining Empty Space of the Cube: a3 - πa3/6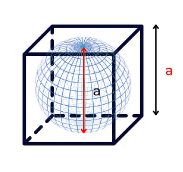
Largest possible cube
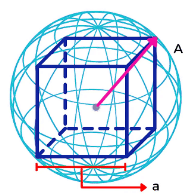
In this type you will be given a sphere of radius “A” cm and will be asked the volume of largest cube which can be chiseled out from it.
Here OA= radius of the sphere. So, diameter of the sphere = 2a
Diagonal of the cube = √3x
(If side of the Square is x)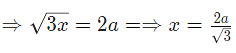
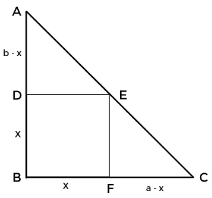
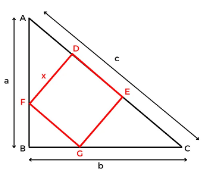
The largest square that can be inscribed in a right angled triangle
In this type you will be given a Square BDEF when one of its vertices coincide with the vertex of the right angle of the triangle ABC
Side of the Square: 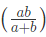
Area of the Square: 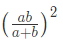
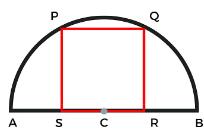
The largest square that can be inscribed in a semi circle
In this type you will be asked the area of the largest Square which can be inscribed in a Semicircle of radius “r”
Area of the Square: 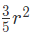
The largest square that can be inscribed in a Quadrant
In this type you can be asked the area or Side of the largest Square which can be inscribed in a Quadrant of Radius “r”
Side of the Square: r/√2
Area of Square: r2/2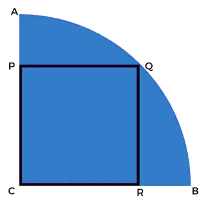
The largest square that can be inscribed in a right angled triangle
In this type you will be given a Square DEGF when one of its vertices coincide with the hypotenuse of the right angle of the triangle ABC and you can be asked for the side of the square.
Side of the Square: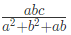
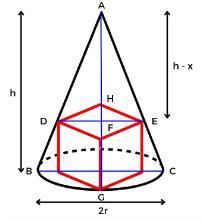
The largest cube that can be chiseled out from a cone
In this question you will be asked about the side of the largest cube which will be chiseled out of a cone of height ‘h’ cm and radius ‘r’ cm
Side of Cube: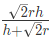
The maximum volume of cylinder
In this you will be asked about the volume of the largest cylinder which can be chiseled out from a right circular cone.
Maximum Volume of the Cylinder: 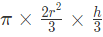

Examples
Q1: Ratan had a hard wooden board out of which he made an equilateral triangle with a side length of 10 cm. Find it’s area?
Ans: The formula to find the area of an equilateral triangle is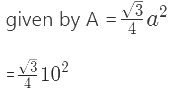
= 43.30cm2
Q2: Sam made a circle out of clay find it’s area in terms of pi given the diameter of circle is 18cm?
Ans: Given Diameter = 18 cm
Radius = 9 cm
Area of circle = πr2
Area = π92
Area= 81πcm2
Q3: The supplement of 90º is?
Ans: Supplementary angles means those angles whose sum is 180.
According to question:
90º + x = 180
= 180- 90 = x
= 90º
Q4: Raj bought a mirror for his room with a length of 12 meters and a diagonal of 15 meters, find the width of the rectangle.
Ans: The width of the rectangle is 9 meters.
In a rectangle, the diagonal divides the rectangle into two congruent right-angled triangles. We can use the Pythagorean Theorem to find the width (‘b’) of the rectangle using the length (‘a’) and the diagonal (‘c’):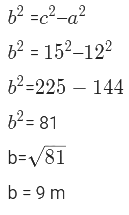
Q5: Find Volume of a ice-cream cone whose radius is 6 cm and height 7 cm?
Ans: We know Volume of cone 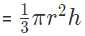
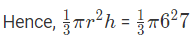
= 84πcm3
|
342 videos|298 docs|185 tests
|
FAQs on Important Formula: Geometry - Quantitative Aptitude for SSC CGL
| 1. What is the formula for finding the area of a triangle? |  |
| 2. How do you calculate the volume of a cube? |  |
| 3. What is the formula for finding the perimeter of a rectangle? |  |
| 4. How do you find the area of a circle? |  |
| 5. What is the formula for calculating the volume of a sphere? |  |






















