SSC CGL Exam > SSC CGL Notes > Quantitative Aptitude for SSC CGL > Important Formulas: Square Roots and Cube Roots
Important Formulas: Square Roots and Cube Roots | Quantitative Aptitude for SSC CGL PDF Download
Square Root
If x2 = y, we say that the square root of y is x and we write √y = x.
Thus, √4 = 2, √9 = 3, √196 = 14.
Cube Root
The cube root of a given number x is the number whose cube is x.
We, denote the cube root of x by x.
Thus, 8 = 2 x 2 x 2 = 2, 343 = 7 x 7 x 7 = 7 etc.
Note:
- √xy = √x x √y
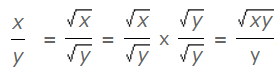
Examples
Example 1: (√625 x 14 x 11 is equal to: 11 √25 √196
(a) 5
(b) 6
(c) 8
(d) 11
Ans: (a)
Given Expression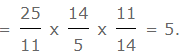
Example 2: How many two-digit numbers satisfy this property. The last digit (unit's digit) of the square of the two-digit number is 8?
(a) 1
(b) 2
(c) 3
(d) None of these
Ans: (d)
A number ending in 8 can never be a perfect square.
Example 3: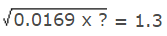 
(a) 10
(b) 100
(c) 1000
(d) None of these
Ans: (b)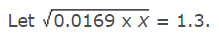
Then, 0.0169x = (1.3)2 = 1.69
⇒ x = 1.69/0.0169 = 100
Example 4: If √5 = 2.236;
Then the value of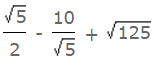 
is equal to:
(a) 5.59
(b) 7.826
(c) 8.944
(d) 10.062
Ans: (b)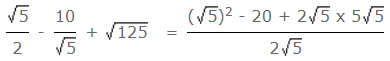
Example 5: The square root of (7 + 3√5) (7 - 3√5) is
(a) 2
(b) 4
(c) √5
(d) 3√5
Ans: (a)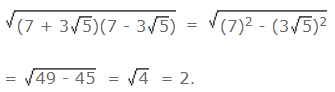
Example 6: What should come in place of both x in the equation:
(a) 12
(b) 14
(c) 144
(d) 196
Ans: (a)
= 8 x 6 x 3
= 144.
∴ x = √144 = 12.
Example 7: The cube root of .000216 is:
(a) .6
(b) .06
(c) 77
(d) 87
Ans: (b)
= 6/102
= 6/100
= 0.06
Example 8: The least perfect square, which is divisible by each of 21, 36 and 66 is:
(a) 213444
(b) 214344
(c) 214434
(d) 231444
Ans: (a)
L.C.M. of 21, 36, 66 = 2772.
Now, 2772 = 2 x 2 x 3 x 3 x 7 x 11
To make it a perfect square, it must be multiplied by 7 x 11.
So, required number = 22 x 32 x 72 x 112 = 213444.
Example 9: If a = 0.1039, then the value of 
is:
(a) 0.1039
(b) 0.2078
(c) 1.1039
(d) 2.1039
Ans: (c)
= (1 - 2a) + 3a
= (1 + a)
= (1 + 0.1039)
= 1.1039
Example 10: A group of students decided to collect as many paise from each member of group as is the number of members. If the total collection amounts to ₹ 59.29, the number of the member is the group is:
(a) 57
(b) 67
(c) 77
(d) 87
Ans: (c)
Money collected = (59.29 x 100) paise = 5929 paise.
Number of members = √5929 = 77.
The document Important Formulas: Square Roots and Cube Roots | Quantitative Aptitude for SSC CGL is a part of the SSC CGL Course Quantitative Aptitude for SSC CGL.
All you need of SSC CGL at this link: SSC CGL
|
315 videos|182 docs|185 tests
|
FAQs on Important Formulas: Square Roots and Cube Roots - Quantitative Aptitude for SSC CGL
| 1. What is a square root? |  |
Ans. A square root is a mathematical operation that calculates the value which, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9.
| 2. What is a cube root? | |
Ans. A cube root is a mathematical operation that calculates the value which, when multiplied by itself twice, gives the original number. For example, the cube root of 8 is 2 because 2 multiplied by 2 multiplied by 2 equals 8.
| 3. How can I find the square root of a number? | |
Ans. To find the square root of a number, you can use the square root symbol (√) or a calculator. If you want to calculate it manually, you can use methods like the long division method or the prime factorization method.
| 4. How can I find the cube root of a number? | |
Ans. To find the cube root of a number, you can use the cube root symbol (∛) or a calculator. If you want to calculate it manually, you can use methods like the estimation method or the prime factorization method.
| 5. What are some real-life applications of square roots and cube roots? | |
Ans. Square roots and cube roots have various applications in real-life scenarios. Some examples include calculating distances in geometry, determining the size of objects, calculating volumes of containers, analyzing growth rates in finance, and estimating probabilities in statistics.
About this Document
4.95/5
Rating
May 18, 2025
Last updated
Document Description: Important Formulas: Square Roots and Cube Roots for SSC CGL 2025 is part of Quantitative Aptitude for SSC CGL preparation.
The notes and questions for Important Formulas: Square Roots and Cube Roots have been prepared according to the SSC CGL exam syllabus. Information about Important Formulas: Square Roots and Cube Roots covers topics
like Square Root, Cube Root and Important Formulas: Square Roots and Cube Roots Example, for SSC CGL 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Formulas: Square Roots and Cube Roots.
Introduction of Important Formulas: Square Roots and Cube Roots in English is available as part of our Quantitative Aptitude for SSC CGL
for SSC CGL & Important Formulas: Square Roots and Cube Roots in Hindi for Quantitative Aptitude for SSC CGL course.
Download more important topics related with notes, lectures and mock test series for SSC CGL
Exam by signing up for free. SSC CGL: Important Formulas: Square Roots and Cube Roots | Quantitative Aptitude for SSC CGL
Description
Full syllabus notes, lecture & questions for Important Formulas: Square Roots and Cube Roots | Quantitative Aptitude for SSC CGL - SSC CGL | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude for SSC CGL | Best notes, free PDF download
Information about Important Formulas: Square Roots and Cube Roots
In this doc you can find the meaning of Important Formulas: Square Roots and Cube Roots defined & explained in the simplest way possible. Besides explaining types of
Important Formulas: Square Roots and Cube Roots theory, EduRev gives you an ample number of questions to practice Important Formulas: Square Roots and Cube Roots tests, examples and also practice SSC CGL
tests
Related Searches
practice quizzes
,Extra Questions
,Exam
,Objective type Questions
,mock tests for examination
,shortcuts and tricks
,Viva Questions
,Important Formulas: Square Roots and Cube Roots | Quantitative Aptitude for SSC CGL
,MCQs
,past year papers
,Important Formulas: Square Roots and Cube Roots | Quantitative Aptitude for SSC CGL
,video lectures
,ppt
,Free
,Summary
,study material
,Semester Notes
,Previous Year Questions with Solutions
,Sample Paper
,Important questions
,Important Formulas: Square Roots and Cube Roots | Quantitative Aptitude for SSC CGL
;
Additional Information about Important Formulas: Square Roots and Cube Roots for SSC CGL Preparation
Important Formulas: Square Roots and Cube Roots Free PDF Download
The Important Formulas: Square Roots and Cube Roots is an invaluable resource that delves deep into the core of the SSC CGL exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Formulas: Square Roots and Cube Roots now and kickstart your journey towards success in the SSC CGL exam.
Importance of Important Formulas: Square Roots and Cube Roots
The importance of Important Formulas: Square Roots and Cube Roots cannot be overstated, especially for SSC CGL aspirants.
This document holds the key to success in the SSC CGL exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Formulas: Square Roots and Cube Roots Notes
Important Formulas: Square Roots and Cube Roots Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Formulas: Square Roots and Cube Roots.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Formulas: Square Roots and Cube Roots Notes on EduRev are your ultimate resource for success.
Important Formulas: Square Roots and Cube Roots SSC CGL Questions
The "Important Formulas: Square Roots and Cube Roots SSC CGL Questions" guide is a valuable resource for all aspiring students preparing for the
SSC CGL exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Formulas: Square Roots and Cube Roots on the App
Students of SSC CGL can study Important Formulas: Square Roots and Cube Roots alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Formulas: Square Roots and Cube Roots,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Formulas: Square Roots and Cube Roots is prepared as per the latest SSC CGL syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup