Important Formula: Fractions & Decimals | Quantitative Aptitude for SSC CGL PDF Download
Number, Decimal and Fraction Formulas
1. (a + b)(a – b) = (a² – b²)
2. (a + b)² = (a² + b² + 2ab)
3. (a – b)² = (a² + b² – 2ab)
4. (a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
5. (a³ + b³) = (a + b)(a² – ab + b²)
6. (a³ – b³) = (a – b)(a² + ab + b²)
7. (a³ + b³ + c³ – 3abc) = (a + b + c)(a² + b² + c² – ab – bc – ac)
8. when a + b + c = 0, then a³ + b³ + c³ = 3abc
Conversion of a Decimal into Vulgar Fraction
Place the digit 1 in the denominator beneath the decimal point and add a corresponding number of zeros to it, equal to the count of digits following the decimal point.
Now, remove the decimal point and reduce the fraction to its lowest terms.
For Ex- 0.45 = 45/100 = 9/25
Annexing Zeros and Removing Decimal Signs
Applying zeros to the extreme right of a decimal fraction does not change its value. Thus, 0.5 = 0.50 = 0.500, etc.
If numerator and denominator of a fraction contain the same number of decimal places, then we remove the decimal sign.
For Ex- 5.879/4.856 = 5879/4856.
Operations Formulas For Number, Decimals and Fractions
- Addition and Subtraction of Decimal Fractions: The given numbers are placed under each other that the decimal points lies in one column. The numbers are so arranged that can now be added or subtracted in the usual way.
Multiplication of a Decimal Fraction By a Power of 10: Shift the decimal point to the right by as many places as is the power of 10.
Thus, 5.9632 x 100 = 596.32; 0.073 x 10000 = 730. - Multiplication of Decimal Fractions: Multiply the given numbers considering them without decimal point. Now, in the product, the decimal point is marked off to obtain as many places of decimal as is the sum of the number of decimal places in the given numbers.
Suppose we have to find the product (.2 x 0.02 x .002).
Now, 2 x 2 x 2 = 8. Sum of decimal places = (1 + 2 + 3) = 6.
.2 x .02 x .002 = .000008 - Dividing a Decimal Fraction By a Counting Number: Divide the given number without considering the decimal point, by the given counting number. Now, in the quotient, put the decimal point to give as many places of decimal as there are in the dividend.
Suppose we have to find the quotient (0.0204 ÷ 17). Now, 204 ÷ 17 = 12.
Dividend contains 4 places of decimal. So, 0.0204 ÷ 17 = 0.0012 - Dividing a Decimal Fraction By a Decimal Fraction: Multiply both the dividend and the divisor by a suitable power of 10 to make divisor a whole number.
For Ex-
Number, Decimal and Fraction Formulas
Suppose some fractions are to be arranged in ascending or descending order of magnitude, then convert each one of the given fractions in the decimal form, and arrange them accordingly.
For Ex- Arrange the fractions, in descending order.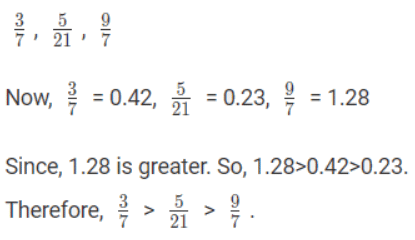
Recurring Decimal
A decimal fraction is termed a recurring decimal when a digit or a group of digits is consistently repeated. In the case of a recurring decimal, a single digit repetition is denoted by placing a dot on it, while a repeated set of digits is represented by placing a bar over the set.
Pure Recurring Decimal
A pure recurring decimal is a decimal fraction where every digit following the decimal point is repeated.
Converting a Pure Recurring Decimal into Vulgar Fraction
Express the recurring digits by writing them once in the numerator, and use a corresponding number of nines in the denominator equal to the count of repeating figures.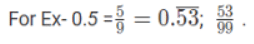
Mixed Recurring Decimal
A decimal fraction in which some figures do not repeat and some of them are repeated, is called a mixed recurring decimal.
Number, Decimal and Fraction Formulas to solve Questions
- Decimal Fractions: Fractions in which denominators are powers of 10 are known as decimal fractions.
Thus, 1/10 = 1 tenth = .1; 1/100 = 1 hundredth = .01;
99 = 99/100 hundredths = .99; 7/1000 = 7 thousandths = .007. - Conversion of a Decimal into Vulgar Fraction: Put 1 in the denominator under the decimal point and annex with it as many zeros as is the number of digits after the decimal point. Now, remove the decimal point and reduce the fraction to its lowest terms.
Thus, 0.25 = 25/100 = 1/4 ; 2.008 = 2008/1000 = 251/125. - Multiplication and Division of Decimal and Fraction: Suppose we have to find the product (.3 x 0.03 x .003).
Now, 3 x 3 x 3 = 27. Sum of decimal places = (1 + 2 + 3) = 6.
.3 x .03 x .003 = .000027
Dividing a Decimal Fraction By a Decimal Fraction:
= 0.00066/0.11
= 0.00066 x 100 /0.11 x 100
= 0.066/11
= .006
Examples
Example 1: √196 × √144 × 20% of 700 = ? + 1265
(a) 22255
(b) 22266
(c) 22588
(d) 25874
Ans: (a)
√196 × √144 × 20% of 700 = ? + 1265
14 × 12 × 140 = ? + 1265
168 × 140 = ? + 1265
23520 = ? + 1265
? = 23520 – 1265
? = 22255
Example 2: 25% of 30% of 850 + 5 × 76 = ?
(a) 441.75
(b) 443.75
(c) 441.57
(d) 443.57
Ans: (b)
25% of 30% of 850 + 5 × 76
= 25/100 * 30/100 * 850 + 5 * 76
= 443.75
Example 3: (32/100) × 750 – ? = (14/100) × 540
(a) 152.6
(b) 132.6
(c) 146.6
(d) 164.4
Ans: (d)
(32/100) × 750 – ? = (14/100) × 540
240 – x = 75.6
x = 240 – 75.6
x = 164.4
Example 4: 4100 + 13.952 – ? = 3764.002
(a) 747.095
(b) 247.752
(c) 347.932
(d) 349.95
Ans: (d)
Let 4100 + 13.952 – x = 3764.002.
Then x = (4100 + 13.952) – 3764.002
= 4113.952 – 3764.002 = 349.95.
Example 5: What is the sum of the decimal fractions 25/100 and 30/100?
(a) 55/100
(b) 65/100
(c) 75/100
(d) 85/100
Ans: (a)
Given decimal fractions: 25/100 and 30/100.
As the denominators are the same in both decimal fractions, we can directly add the numerators.
Thus,
(25/100) + (30/100) = (25 + 30)/100
(25/100) + (30/100) = 55/100.
Hence, the sum of the decimal fractions 25/100 and 30/100 is 55/100.
|
317 videos|299 docs|156 tests
|
FAQs on Important Formula: Fractions & Decimals - Quantitative Aptitude for SSC CGL
| 1. What are some important formulas for numbers, decimals, and fractions? |  |
| 2. How do you convert decimals to fractions? |  |
| 3. What is the difference between a fraction and a decimal? |  |
| 4. How do you add or subtract fractions? |  |
| 5. How do you multiply or divide fractions? |  |
















