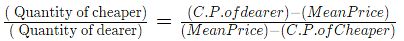Solved Examples: Mixtures & Alligations | Quantitative Aptitude for SSC CGL PDF Download
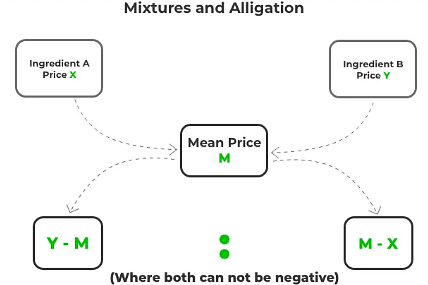
Alligation Methods
Alligation Medial is employed to compute the quantity of a mixture, while Alligation Alternate is utilized to determine the quantity of each ingredient necessary for creating a mixture.
Alligation and Mixture Rules
- If two different ingredients are assorted in a proportion, then

- Furthermore, it can be presented as:

- (Cheaper quantity): (dearer quantity) = (d – m): (m – c)
- Repeated Dilution: If a barrel contains ‘a’ units of liquid out of which ‘b’ units are removed and substituted by water. Then, after ‘n’ processes, the amount of liquid,
=[x(1–y/x)n]units - Furthermore, it is used to analyze the quantity of pure liquid left after ‘n’ number of procedures of constant substitution is prepared on the pure quantity.
Examples
Example 1: A cheater shopkeeper confesses to sell his pulses at cost price but he mixes it with pebbles and thereby gains 25%. The percentage of pebbles in the mixture is:
(a) 14%
(b) 16%
(c) 20%
(d) 25%
Ans: (c)
As per the formula if two materials are mixed, then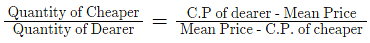
Let C.P. of 1 kg pulse be Re. 1
Then, Selling Price of 1 kg of mixture = Re. 1, Gain = 25%.
C.P of 1kg mixture 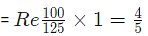
By the rule of allegation, we have:
Ratio of pulse to pebble 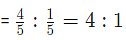
Therefor, % of pebble in the mixture 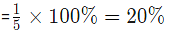
Example 2: Sugar cost INR 130 per kilogram and INR 139 per kilogram are combined along a new type in the ratio 1 : 1 : 2. If the combination is cost Rs. 163 kilogram, then find out the price of the new type per kilogram ?
(a) 170.50
(b) 179.50
(c) 185.50
(d) 191.50
Ans: (d)
Since first and second types are mixed in equal proportions.
So, their average price 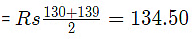
So, the combination is made by mixing two types, one at Rs. 134.50 per kg and another one at INR x in the ratio 1 : 1. We have to find x.
As per the law of allegation:
x−163=28.50
x=191.50
Example 3: A vessel is filled with liquid, 3 parts of which are water and 5 parts syrup. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup?
(a) 1/6
(b) 2/5
(c) 1/5
(d) 3/5
Ans: (c)
Given:
A vessel is filled with liquid, 3 parts of which are water and 5 parts syrup.
3 parts water and 5 parts syrup.
So water = 3/8 and syrup = 5/8
To make them equal,
Skill Academy
4/8 of water and syrup should be there
Let x be the amount of liquid we replace by water,
Water = 3x/8 and Syrup = 5x/8
Now,
Water before replacement + 5x/8= syrup before replacement - 5x/8
⇒ syrup-water(before replacement) = 10x/8 5x/4
⇒ 5/8 part-3/8 part = 5x/4
⇒1/4 part = 5x/4
⇒ x =1/5
So, 1/5 of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup.
Example 4: In what proportion must kerosene be mixed with petrol to earn 16(2/3)% if we sell the combination at cost price?
(a) 2: 7
(b) 6: 1
(c) 2: 3
(d) 1: 6
Ans: (d)
Assume price of 1 litre petrol= INR 1
Selling price of 1 litre mix=1 rs.
Profit= 5/3percent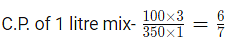
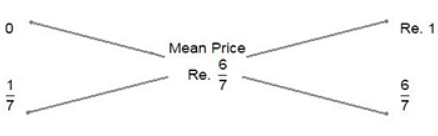
Thus proportion of kerosene and petrol = 1/7 : 6/7 = 1 : 6
Example 5: A pot contains 40 litres of Mint juice. 4 litres of Mint juice is replaced with Honey. This is done two times more. Find out the quantity of Mint juice which is in the pot now?
(a) 29.16
(b) 30.15
(c) 32.43
(d) 33.19
Ans: (a)
As per the allegation formula
=x(1−y/x)n = x(1−y/x)n units.
So, milk in the pot now =40(1−4/40)3 = 40(1−1/10)3 =29.16
Example 6: A vessel comprises 100 litres of fresh juice. Out of this vessel 12 litres of juice was pulled out and changed by water. This whole process was done two more times. Now calculate the quantity of fresh juice contained by the vessel?
(a) 64.12
(b) 65.87
(c) 68.14
(d) 69.54
Ans: (c)
Amount of fresh juice left after 3 times 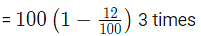
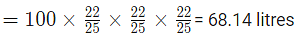
Example 7: A deals in two types of black-eyed peas. Each costing INR 14 and INR 21 per kg. What ratio should the both types be mixed to get a combination worth INR18.50 per kg.
(a) 5:9
(b) 5:7
(c) 7:5
(d) 5:3
Ans: (a)
According to the rule of allegation:
Required rate = (21 - 18.50) : (18.50 - 14)
Price of second black-eyed peas-mean price: Mean price-cost of first black-eyed peas
2.50 : 4.50 = 5 : 9.
Example 8: Two jugs X and Y having coca cola and water mixed in the proportion 5: 2 and 7: 6 respectively. Now if we want a new mixture in jug Z having coca cola and water in the proportion of 8:5 then what will be the ratio?
(a) 5:6
(b) 3: 4
(c) 6: 7
(d) 7: 9
Ans: (d)
Let P unit of the first mixture is added to Q unit of the second mixture.
So, in P unit of first mixture,
Amount of milk present = 5/7 * P = 5P/7
Amount of water present = 2/7 * P = 2P/7
So, in Q unit of second mixture,
Amount of milk present = 7/13 * Q = 7Q/13
Amount of water present = 6/13 * Q = 5Q/13
According to the question,
(5P/7 + 7Q/13) ÷ (2P/7 + 6Q/13) = 8/5
⇒ 325P + 245Q = 208P + 336Q
⇒ 117P = 91Q
⇒P: Q = 91:117 = 7:9
Example 9: A fixed amount of water is mixed with Sangria costing Rs 12 per litre. The rate of mixture is Rs 8 per litre. Find out the proportion of water and Sangria in the new combination.
(a) 3:2
(b) 4:3
(c) 1:2
(d) None of the above
Ans: (c)
1 litre of water C.P. = Rs 0.
1 litre of Sangria C.P. = Rs 12.
Mean Price = Rs 8.
As per the Allegation formula: (Amount of Cheaper):(Amount of Dearer) = (CP of dearer - Mean Price):(Mean Price - CP of cheaper)
Therefore, Water: Sangria = (12-8):(8-0) = 4:8 = 1:2.
Example 10: A sells 3 types of mustard seeds at the price of INR 126 per kg and INR 135 per kg and 3rd variety in the ratio of 3 : 2 : 5. If the cost of the final mix is INR 155 per kg, find the rate of third type of mustard seeds.
(a) 170.54
(b) 195.43
(c) 180.40
(d) 190.76
Ans: (c)
Assume that the Third type of mustard seed quantity is X.
Then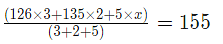
on solving
648 + 5x = 10 x 155
5x = 1550-648
x=902/5
X= 180.40
|
314 videos|170 docs|185 tests
|
FAQs on Solved Examples: Mixtures & Alligations - Quantitative Aptitude for SSC CGL
| 1. What is a mixture? |  |
| 2. How is the concentration of a mixture calculated using alligation? |  |
| 3. Can alligation be used to solve problems involving medications or solutions? |  |
| 4. What is the purpose of using alligation in industries? |  |
| 5. Can alligation be applied to solve problems related to cost or price mixtures? |  |
|
314 videos|170 docs|185 tests
|

|
Explore Courses for SSC CGL exam
|

|