Solved Examples: Probability | Quantitative Aptitude for SSC CGL PDF Download
Formula of Probability
 Probability is a way of understanding and quantifying how likely or unlikely something is to happen based on the information we have.
Probability is a way of understanding and quantifying how likely or unlikely something is to happen based on the information we have.
Important points related to Solving Probability Questions
- Probability ranges from 0 to 1: The probability of an event can never be less than 0 (impossible event) or greater than 1 (certain event).
- Sample Event: The sample space is the set of all possible outcomes of an experiment or random event.
- Event: An event is a subset of the sample space, representing a specific outcome or a combination of outcomes.
The total of the chances of all regular actions should be 1.
If the action’s possibility is near to 1, the probabilities of an action to happen will be more.
If the chances of the event is near to 0, the probabilities of an incident to happen will be lesser in number. - Addition rule: The probability of the union of two events A and B (A or B) is calculated by adding their individual probabilities and subtracting the probability of their intersection (A and B).
- Multiplication rule: The probability of the intersection of two independent events A and B (A and B) is calculated by multiplying their individual probabilities.
Examples
Example 1: In a group of 80 men and 40 women, half of total men and half of total women know basketball. Find the probability of choosing one man or woman who knows basketball?
(a) 2/3
(b) 1/2
(c) 14/7
(d) 16/9
Ans: (b)
Total men and women in group = 80 + 40 = 120
Let X be the event that the chosen person is men and Y be the event that the chosen person is women knowing basketball.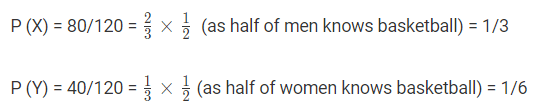
Therefore, P (X or Y) = P (X) + P (Y)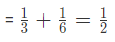
Example 2: What is the probability of choosing either a heart or a face card from a 52 card deck?
(a) 11/13
(b) 10/26
(c) 11/26
(d) 14/29
Ans: (c)
Probability of drawing a heart (E) = 13/52 =1/4
The probability of drawing a face card (4 kings, 4 queens, 4 jacks) (F) = 12/52 = 3/13
The probability of either a face card or a heart required to be added separately. However, do not forget to subtract three face cards of heart in order not to count them two times.
The probability of drawing (face card and heart) = 3/52
Probability of selecting either a heart or a face P (E or F)
= P (E or F) = P (E) + P (F) - P (E and F)
= 1/4 + 3/13 - 3/52 = 22/52 = 11/26
Example 3: A girl has a bag filled with five green, three pink, and four purple chocolates. If one chocolate is taken out randomly from the bag, substituted, and the procedure is continued two more times. Then find the probability of taking out two green chocolates and one purple chocolate?
(a) 16/243
(b) 25/432
(c) 19/240
(d) 21/241
Ans: (b)
Total chocolates = 5 green + 3 pink + 4 purple = 12
The probability of taking out one green chocolate = 5/12
The probability of taking out another green chocolate = 5/12
The probability of taking out one purple chocolate = 4/12
The probability of taking out two green chocolates and one purple chocolate = 5/12 × 5/12 × 4/12
= 100/1728
= 25/432
Example 4: Two dice are turned together. Find the probability that the total is equals to one, seven, and less than twelve?
(a) 0, 6/36, 35/36
(b) 1/6, 5/36, 33/36
(c) 2/5, 4/5, 9/11
(d) None of the above
Ans: (a)
The sample space of two dice rolled together is:
S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }
Therefore, it is clear that there are no outcomes in which the total of two dices are 1. Thus the probability = P(E) = n(E) / n(S) = 0 / 36 = 0
The probability of having the sum as seven = {(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}, hence,
P(E) = n(E) / n(S) = 6 / 36
Except one outcome, which is { (6,6) } all other are equals to less than twelve.
P(E) = n(E) / n(S) = 35 / 36
Therefore, the probabilities are: 0, 6/36, 35/36
Example 5: A bag comprises of eight white balls and twelve blue balls. If a ball is chosen randomly from the bag. Find the probability of receiving a blue ball and no blue ball?
(a) 6/5 and 2/5
(b) 5/9 and 3/5
(c) 10/11 and 2/3
(d) 3/5 and 2/5
Ans: (d)
White balls = 8
Blue balls = 12
Total = 8 white + 12 blue = 20 balls
The probability of receiving a blue ball = 12/20 or 3/5
The probability of not receiving blue ball = 1 - Probability of receiving the blue ball
= 1 - 3/5
= 2/5
Example 6: A bag has some green balls and 40 orange balls. If the probability for taking out the green balls is 7/10 of the orange ball, then find out how many green balls are there in the bag?
(a) 28
(b) 12
(c) 29
(d) 40
Ans: (a)
Let us assume the green balls as z
Orange ball = 40
Total balls= z + 40
P (green balls) = z/z +40
P (orange balls) = 40/z+40
According to the question,
P (green balls) = 7/10 P (orange ball)
z/z + 40 = 7/10 × 40/z + 40
z = 7/10 × 40
z = 28
Example 7: A packet contains 15 identical tube lights. Among them, 6 are defective, and 9 are not. Find the probability that a tube light selected from 15 randomly is the defective one?
(a) 2/3
(b) 1/3
(c) 2/5
(d) 1/5
Ans: (c)
P (S) = Total lights
P(S) = 15
P(E) = Defective light
P(E) = 6
Therefore, the probability of selecting a defective light = P(S)/P(E)
= 6/15 = 2/5
Example 8: A group of 6 players is selected randomly among a group of 12 men and 6 women. Determine the probability of exactly 3 women in the group?
(a) 400/999
(b) 1100/4641
(c) 312/1251
(d) 550/1983
Ans: (b)
There are overall 18 players = 12 men and 6 women.
Therefore three women can be selected from 6 in 6C3 ways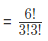
= 20 ways.
Three men can be selected in 12C3
= 220 ways.
Thus total selections for the favorable cases = 20 x 220 = 4400 ways.
The sample space will cover total cases of 6 people chosen from 12 men and 6 women = (12 + 6 = 18) people that is 18C6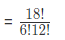
= 18564
So probability = (favourable cases)/(Sample space)
= 4400/18564
= 1100/4641
Example 9: If two dices are rolled together, then find the probability that the total of two dice will be greater than 8 if the first dice is rolled is a 6?
(a) 1/2
(b) 2/5
(c) 2/3
(d) 1/9
Ans: (c)
Given first dice = 6 means Sample Space Now = {(6, 1)(6,2), (6, 3) (6, 4) (6, 5) (6, 6)}
Total of two dice > 8 = ((6, 3) (6, 4) (6, 5) (6, 6))
Required Probability = 4/6 = 2/3
Example 10: In a team of 50 boys and 18 girls, half of the boys and half of the girls know the volleyball. What is the probability of selecting one person who is either boy or girl knowing volleyball?
(a) 353/289
(b) 153/289
(c) 253/289
(d) None of the above
Ans: (d)
Total number of boys and girls = 50 + 18 = 68
Let B be the event that the selected person is a boy and G be the event that the selected person is a girl knows the cricket.
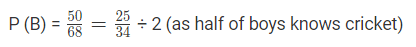

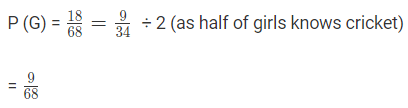
Therefore, P (B or G) = P (B) + P (G)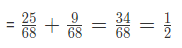
|
342 videos|298 docs|185 tests
|





















