Understanding Important Concepts in Logical Reasoning - Italian PDF Download
| Table of contents |

|
| Introduction |

|
| Logic and Language |

|
| Symbolic Logic |

|
| Notes on Interpretation |

|
| Tips and Tricks |

|
Introduction
In logical reasoning, there are key principles that help in solving problems. The main objectives include learning essential rules for solving logical reasoning questions, thinking in a structured manner, dealing with complexities in problem-solving, and organizing information visually to better understand the problem.

Logic and Language
Logic is a fundamental aspect of our lives, present in both human and natural activities. It ranges from everyday logical thinking to advanced forms that operate machinery. Our actions, studies, creations, and activities are all guided by inherent logic.

The Roots of Logic and Language: The ancient Greeks were the first to deeply study logic. Initially, the lack of a systematic notation led them to rely on language to explain logic. Even today, we instinctively use language to convey logical ideas. Examples include providing directions, explaining locations of items, or describing cause-and-effect relationships.
Everyday Logic: In daily life, we constantly apply logic, such as when starting a car or using household appliances. Logical language is used to explain these actions. The Greeks primarily focused on documenting logical language in their study of logic. However, using language to understand complex logical processes became challenging, leading to difficulties in comprehending Aristotle's Treatise on Logic in the 4th century BC.
Symbolic Logic
What is Symbolic Logic?
Symbolic logic is a way of expressing logical ideas using symbols and variables instead of regular language.
Unlike English, which can be imprecise and lead to multiple interpretations, symbolic logic uses specific symbols to convey statements with a clear truth value – either true or false.
Instead of relying on potentially ambiguous sentences, symbolic logic provides a more structured and accurate means of expressing logical concepts.
It helps avoid confusion and ensures a definite understanding of the intended meaning.
List of Symbolic Logic Symbols
Symbolic logic uses several symbolic logic symbols, called operators, each with its own unique meaning.
These include the following:
- ∀, the universal quantifier, read as for all
- ∃, the existential quantifier, read as there exists
- ∧, denoting conjunction, read as and
- ∨, denoting disjunction, read as or
- →, denoting implication, read as implies, or when written in the form P→Q, read if P, then Q
- ⇔, denoting biconditional, read as if and only if
 Operators and their meanings
Operators and their meanings - ¬, denoting negation, read as not
- ⊕ XOR operator
- ~ NOT operator
- + AND operator
Note:- Proper nouns should always be denoted by capitals.
- Create your own set of symbols for standard relational sentence structures.
- Where the gender of proper noun is is important to solve the questions, denote the female by underlining the capital letter used.
Symbolic Logic Examples
Learning how to solve symbolic logic problems requires practice, so the following worked-out examples are presented:
Example 1
The goal is to convert the following sentence into symbols: ''Michelle will make dinner if Jack does not, and only if Jack does not.'' First, symbolize ''Michelle makes dinner'' as M and ''Jack makes dinner'' as J. Then, write M⇔¬J, since the ''only if'' part of the sentence indicates a biconditional.
Example 2
The goal is to convert the following sentence into symbols, just as before: ''The economy will improve if the deficit is reduced, but the deficit will be reduced only if government spending does not increase and taxes are raised.'' If G denotes ''the deficit will be reduced,'' D denotes ''the economy improves,'' E denotes ''government spending increases,'' and G denotes ''taxes are raised,'' then the sentence can be converted into symbols. The major component of this complex sentence is the ''but,'' which can be logically expressed as ∧. It is then written as (D → E) ∧ (D → (¬G ∧ T)).
(1) If, Then
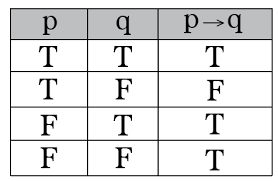 If then Truth Table
If then Truth Table
The condition If A, then B leads to the following valid conclusions.
- Valid Reasoning 1: A therefore B.
- Valid Reasoning 2: Not B, therefore not A.
At the same time If A then B also throws up the following invalid conclusions.
- Invalid Reasoning 1: B, therefore A.
- Invalid Reasoning 2: Not A, therefore not B.
The above structures of logical thought can be illustrated through the following examples:
If A teaches, B will go to the movies.
- Valid Reasoning 1: A teaches, therefore B will go to the movies.
- Valid Reasoning 2: B has not gone to the movies, therefore A did not teach.
- Invalid Reasoning 1: B went to the movies, therefore A must have taught. This is an invalid line of reasoning.
- Invalid Reasoning 2: A did not teach, therefore B did not go to the movies. This too is invalid.
(2) If and Only If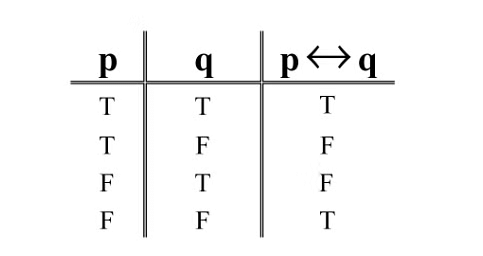 If and Only If Truth TableThe condition If and Only If A, then B leads to the following valid conclusions.
If and Only If Truth TableThe condition If and Only If A, then B leads to the following valid conclusions.
- Valid Reasoning 1: A, therefore B.
- Valid Reasoning 2: Not B, therefore not A.
- Valid Reasoning 3: B therefore A.
- Valid Reasoning 4: Not A therefore not B.
The above structures of logical thought can be illustrated through the following examples:
If and only if A teaches, B will go to the movies.
- Valid Reasoning 1: A teaches, therefore B will go to the movies.
- Valid Reasoning 2: B has not gone to the movies, therefore A did not teach.
- Valid Reasoning 3: B went to the movies, therefore A must have taught.
- Valid Reasoning 4: A did not teach, therefore B did not go to the movies.
(3) Either Or
Either A or B
- Valid Reasoning 1: Not A then B
- Valid Reasoning 2: Not B then A
- Valid Reasoning 3: A then Not B
- Valid Reasoning 4: B then Not A
The above structures of logical thought can be illustrated through the following examples:
Either A teaches or B goes to the movies.
- Valid Reasoning 1: A does not teach, therefore B will go to the movies.
- Valid Reasoning 2: B has not gone to the movies, therefore A must have taught.
- Valid Reasoning 3: A taught, then B did not go to the movies.
- Valid Reasoning 4: B went to the movies, then A did not teach.
(4) If, Then Not
If A then Not B:
- Valid Reasoning 1: A then not B
- Invalid Reasoning 1: Not B then A Valid Reasoning 2: B then Not A
The above structures of logical thought can be illustrated through the following examples:
If A teaches, then B will not go to the movies.
- Valid Reasoning 1: A teaches, therefore B will not go to the movies.
- Invalid Reasoning 1: B has not gone to the movies, therefore A taught.
- Valid Reasoning 2: B went to the movies, therefore A did not teach.
As a student, it's crucial to follow specific steps when tackling logical questions:
- Begin by thoroughly understanding the context through a complete preview of the situation.
- Read each part of the question attentively, concentrating on every word. This focus is essential, especially in lengthy sentences, where individual words can significantly impact the meaning. Ignoring these words may lead to errors in logic and deduction.
- Let us now proceed to understand how all this applies to real life problem solving through examining questions which have been asked in different competitive exams and CAT.
Example 1: A party was held at the house of the Mehtas. There were five other couples present (besides Mr and Mrs Mehta), and many, but not all, pairs of people shook hands. Nobody shook hands with anyone twice, and nobody shook hands with his/her spouse. Both the host and hostess shook some hands.
At the end of the party, Mr Mehta polled each person present to see how many hands each person (other than himself) shook. Each person gave a different answer.
Determine how many hands Mrs Mehta must have shaken.
Can we prove that it was not Mrs Mehta who shook 10 hands?
Solution: Let there be 5 couples:
A - A
B - B
C - C
D - D
E - E
and M - M
Deduction 1: From the condition that nobody shook hands with his/her spouse, it is clear that none of the twelve people in the party shook more than 10 hands.
(Since, nobody shakes hands with himself or his/her spouse, it leaves a maximum of 10 people to shake hands with).
Deduction 2: Mr Mehta has asked the question to eleven different people and each of them has given a different answer. Also, the highest answer anyone could have possibly given is 10. Hence, the only way to distribute different numbers of hand shakes amongst the 11 people is:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. [Note: somebody shook 0 hands and somebody shook 10].
Deduction 3: Since the host and hostess have both shaken some hands, the person who shook "O' hands cannot be either M or M. It has to be one of the other 10 people in the party.
[At this point you need to realise that in the context of this problem A, A. B, B, C, C, D, D, E and E are alike, i.e. there is no logical difference amongst these 10 and you have exactly the same information about each of these 10 people. However, Mrs Mehta is different because she stands out as the hostess as well as the wife of the person who has asked the question].
Since all ten guests are the same, assume "A' shook no hands. This leads us to the following deduction.
Deduction 4: Take any one person apart from A and A; say B. B will not shake hands with himself and his wife.
Besides, B will also not shake hands with A (who has shaken no hands). Thus, B can shake a maximum of 9 hands and will thus not be the person to shake 10 hands.
What applies to B, applies to B, C, C, D, D, E, E and M.
Hence, A is the only person who could have shaken 10 hands. Hence, amongst the couple A and A, if we suppose that A had shaken 0 hands, then A must have shaken 10 hands.
Note: The main result here is that, out of the people to whom M has asked the question, and amongst whom we have to distribute the numbers 0 to 10, there has to be a couple who has had 0 and 10 handshakes. It could be any of the five couples, but it cannot be M who has either 0 or 10 handshakes.
We now proceed, using the same line of reason as follows.
Deduction 5: Suppose B has l handshake — he must have shaken hands with A (who has shaken everybody's hands she can).
Then, B wouldn't have shaken hands with anyone out of A, B,C,C, D, D, E, E and M. At this point the following picture emerges: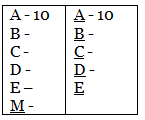
Numbers left to be allocated — 2, 3, 4, 5, 6, 7,8, 9.
Considering C, as a general case, he cannot shake hands with C, A (who shook no hands) and B (who shook hands only with A. This is mandatory since A has shaken hands with 10 people).
Thus, C can shake hands with a maximum of 8 people and this deduction will be true for C, D, D, E, E and M too.
Hence, the only person who could get 9 handshakes is B.
Thus, we conclude that just like 0 and 10 handshakes were in one pair, similarly 1 and 9 handshakes too have to be part of one pair of husband and wife.
Similar deductions will lead to the realisation that 2 and 8, 3 and 7 and 4 and 6 handshakes will also occur for couples amongst the 11 people questioned.
Hence, M must have shaken 5 hands.
Notes on Interpretation
When it comes to solving reasoning-based questions, Trial and Error is a highly useful method. There are three main ways to conduct a trial and error search:

- Complete trial and error.
- Directed trial and error.
- Blind trial and error.
Many students often use blind trial and error, which hinders their ability to solve logical questions. By not applying deductive logic for a more focused search, they find themselves going in circles while attempting to solve such questions. In contrast, directed trial and error, as well as comprehensive trial and error, are more effective problem-solving approaches and therefore, are preferable over the
complete trial and error method.
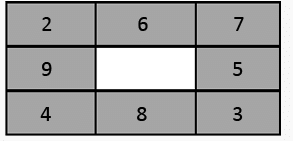
Example 2: 44 people live in eight houses (3 on each side of the Albert Square). Each house has a different number of people living in it. Each line of three houses has 15 people living in it. How many people live in each house?
Solution: Simplifying, we have to get 4 sets of numbers, each of which add up to 15. So start guessing.
The average number of people in a house is 44/8 is roughly 4.5. So what numbers should we take? 2, 3, 4, 5, 6, 7, 8, 9. Now, we should also have an average close to 5 for each set.
Let's start:
- Set 1: 3, 5, 7
- Set 3: 2, 4, 9
- Now, the other two sets will have an overlap. So let's guess the overlaps:
- Set 2: Overlaps are 2 and 7. So the third number will be 6. That's great! Because we have not used 6 yet.
- Set 4: Overlaps are 3 and 9. Then the third number ends up to 3 again. Wrong guess! So we need to try again. Overlaps are 3 and 4. In this case third number works out to be 8, which we have not used. Wonderful!
- So here is the answer
Example 3: Let us now consider another question, which is a classic case of complete or comprehensive trial and error method.
Two people A and B are playing a game. Both A and B are logical people. There are two boxes on the table. One of them contains 9 balls, the other contains 4 balls. In this game, the players are supposed to take alternate turns of picking up balls according to the following rules:
(a) Pick up as many balls as you want to from any box.
(b) Pick up an equal number of balls from both boxes. (if you pick from both boxes).
The person who picks up the last ball wins the game.
In his/her turn, it is mandatory to pick up at least one ball.
A has to play first. What should he do to ensure a win?
Solution:
Deduction 1: The rules of the game define that there are two legal moves:
Picking up an equal number from each box or picking up any number from either box (at least 1).
Deduction 2: A has 17 possible moves to make and since the question asks for one particular move that will ensure a win, one of these 17 must be the winning move. It is at this stage that you should realise that the question calls for a comprehensive trial and error which should result in the elimination of 16 possibilities.
The starting position is 9, 4.
A's options at the start of the game can be basically divided into three options:
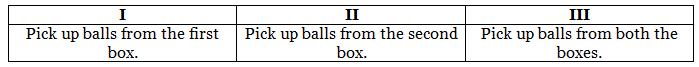
The position after A plays his move can be documented as follows (in terms of the number of balls B has in front of him.):
[There are 9 moves in option I.] (Balls from first box are picked by A.) If
- A picks up 1 ball, B will be left with 8, 4.
- A picks up 2 balls, B will be left with 7, 4
- A picks up 3 balls, B will be left with 6, 4
- A picks up 4 balls, B will be left with 5, 4
- A picks up 5 balls, B will be left with 4, 4
- A picks up 6 balls, B will be left with 3, 4
- A picks up 7 balls, B will be left with 2, 4
- A picks up 8 balls, B will be left with 1, 4
- A picks up 9 balls, B will be left with 0, 4
Similarly, if he picks up balls from the second box (option II) he will have an end result of: If
- A picks up 1 ball, B will be left with 9, 3
- A picks up 2 balls, B will be left with 9, 2
- A picks up 3 balls, B will be left with 9, 1
- A picks up 4 balls, B will be left with 9, 0 And for option III, If:
- A picks up 1 ball each from both boxes, B is left with 8, 3
- A picks up 2 balls each from both boxes, B is left with 7, 2
- A picks up 3 balls each from both boxes, B is left with 6, 1
- A picks up 4 balls each from both boxes, B is left with 5, 0
Out of these 17 options, the options of leaving (0, 4), (9, 0) and (5, 0) are infeasible, since it will result in an immedi-ate win for B who can clean up the board in one move.
Similarly, leaving (4, 4) will also cause an immediate win for B. This leaves A with 13 options which he needs to consider. These are:
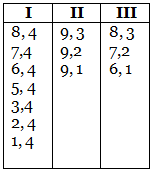
From these 13, the easiest option to check is (1, 4). If B gets (1, 4) he has the following options:

Obviously, he cannot play (0, 4), (1, 0), (1, 1) or (0, 3).
This means he can leave A with (1, 2) or (1, 3). These need to be further investigated.
If B leaves (1, 2), A has the following options to leave for B:
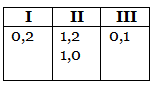
Obviously, if he plays any of this, A will lose. Hence, if B leaves A with (1, 2), A will definitely lose.
Deduction 3 A cannot leave B with a situation in which
B can make into (1, 2) or (2, 1).
Evaluating the 13 options left for A, we get that (1, 4), (2,4), (3, 4), (5, 4), (9, 1), (9, 2), (6, 1) and (1, 2) are situations from which B can reach (2, 1) or (1, 2) in one move.
This means B will win if A leaves him with any of these eight situations.
Thus, A will eliminate these eight options from his list of 13 and come down to five options which need further checking. These are: (6, 4), (7, 4), (8, 4), (9, 3) and (8, 3).
At this stage we further need to eliminate four of these five options to come to the correct answer.
Now let us start our investigation with (6, 4). If B is left with (6, 4) he has the following options:
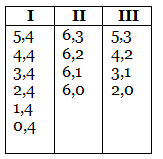
Of this, B cannot play (0,4), (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 0), (6, 1), (6, 2), (2, 0), (3, 1) and (4, 2) [since these lead to a (2, 1) or a clean win in one move]. Thus, B can either leave (6, 3) or (5, 3).
If B leaves (5, 3) for A, A's options are:
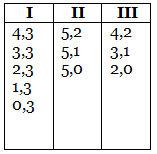
In each of these cases, B will either win in one move or get to (2, 1) in one move. Thus, A cannot do anything if B leaves (5, 3) in return for A leaving (6, 4).
Deduction 4 Just like being left with (2, 1) means a definite loss, so does being left with (5, 3).
Hence, A cannot allow a situation in which B can make it (5, 3) in one move.
Thus, A cannot leave B with (6, 4), (9, 3) or (8, 3) since, each of these will result in B giving back (5, 3) in
one move.
Thus, A's option are down to (7, 4) or (8, 4). These need to be further investigated now:
Let us consider A leaving (7, 4) for B.
B's options are:
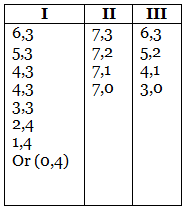
After closely evaluating each of these, all possible options will get eliminated because in one move they lead to either a straight win or a (2, 1) situation or a (5, 3) situation.
If A does any of this, then B cannot do anything to stop from losing the game.
The above question obviously is extremely long and complicated. However, what needs to be noticed is that even for this extremely long question, at no point of time is there any big logical jump, i.e., from one logic emerges the next one and so on.
Tips and Tricks

- Tip #1: Know the type of question you're dealing with, like deduction, inference, assumption, or pattern recognition. This understanding helps you approach the problem more strategically.
- Tip #2: Break down the information into smaller parts and analyze it. Identify main points, assumptions, and conclusions to better grasp the problem.
- Tip #3: For certain question types, like sequencing or spatial reasoning, draw diagrams to visualize and solve non-verbal reasoning problems more easily.
- Tip #4: Use the process of elimination to narrow down options. Eliminate clearly incorrect choices to focus on finding the correct answer more quickly.
- Tip #5: Watch out for common logical mistakes, like ad hominem attacks or hasty generalizations. Recognizing these errors helps you avoid falling into traps.
- Tip #6: Manage your time wisely. Logical reasoning questions can be time-consuming, so allocate your time effectively and don't dwell too long on a single question.
- Tip #7: Regular practice is essential. Attempt various types of reasoning questions to build confidence. Use online resources, books, or mock tests for practice.
- Tip #8: Stay calm and focused during a test. Overthinking or stressing can impact logical thinking. Trust your preparation and stay confident.
- Tip #9: If time allows, review your answers. Double-check your reasoning to avoid calculation or assumption errors.
- Tip #10: Learn from mistakes. Analyze errors after practice tests to understand and avoid repeating them, ultimately improving your logical reasoning skills.
FAQs on Understanding Important Concepts in Logical Reasoning - Italian
| 1. Cos'è la logica simbolica e qual è il suo ruolo nel ragionamento logico? |  |
| 2. Quali sono alcune delle principali regole di interpretazione nella logica simbolica? |  |
| 3. Quali sono alcuni suggerimenti e trucchi utili per affrontare concetti importanti nel ragionamento logico? |  |
| 4. Qual è l'importanza di comprendere concetti chiave nella logica e nel linguaggio per il successo nell'esame? |  |
| 5. Qual è il ruolo della logica nel processo decisionale e nella risoluzione dei problemi? |  |



















