Tips and Tricks: Quadratic Equations | Quantitative Aptitude for SSC CGL PDF Download
Tips and shortcuts to solve the Quadratic Equation questions
In order to find the sign of roots we use sign given in the equation.

For example: x2 + 3x – 4 = 0
The factors are 4 and 1
Now will find the sign of roots. According to the table, if sign given in the equation is + and – then their sign of roots is – and +. Therefore, the roots of the equation are -4 and 1

Type 1: Tricks and Shortcuts for Quadratic Questions
When one equation has positive roots while the other has negative roots, or when both equations have roots of the same sign, compare the roots to determine the relationship between them.
Q1: Find the correct option given below by solving the following equation x2 – 7x + 10 = 0 and y2 + 8y + 15 = 0
(a) x < y
(b) x > y
(c) x ≤ y
(d) x ≥ y
Ans: (b)
x2 – 7x + 10 = 0…. (1)
Roots of first equation are 5 and 2
Using the table above, we will find the sign of roots. If sign given in the equation is – and + then their sign of roots is + and +
Therefore, the roots of the equation are 5 and 2
Now, y2 + 8y + 15 = 0 ……. (2)
Roots of second equation are 3 and 5
If sign given in the equation is + and + then their sign of roots is – and –
Therefore, the roots of the equation are -3 and – 2
Now, here roots are +x1, + x2, – y1, and – y2
This clearly shows that X roots are positive and Y roots are negative. So, x> y
Type 2: Tips and Tricks To Solve Quadratic Equations Questions
When roots of the equation are positive and negative and we cannot find the relation between them.
Q2: Find the correct option given below by solving the following equation 6x2 + 11x – 35 = 0 and 6y2 + 5y – 6 = 0
(a) x < y
(b) x > y
(c) x ≤ y
(d) cannot be determined
Ans: (d)
6x2 + 11x – 35 = 0…. (1)
Roots of first equation are 3.5 and 1.66
Using the table above, we will find the sign of roots. If sign given in the equation is + and – then their sign of roots is – and +
Therefore, the roots of the equation are – 3.5 and 1.66
Now, 6y2 + 5y – 6 = 0 ……. (2)
Roots of second equation are 1.5 and 0.66
If sign given in the equation is + and – then their sign of roots is – and +
Therefore, the roots of the equation are – 1.5 and 0.66
Now, here roots are -x1, + x2, – y1, and + y2
It means x2> – y1 and –x1< + y2
So, we cannot determine which roots are greater.
Type 3: Tips and Tricks and Shortcuts for Quadratic Questions
When we can find a equation where x is a variable and a, b, and c represent constants and D, i.e., Discriminant.
The discriminant is the part of the quadratic formula underneath the square root symbol: b²-4ac.
Q3: Find the Discriminant and roots of the following equation: 3x2 − 5x − 7 = 0.
Sol:
Let us find Discriminant, 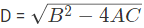
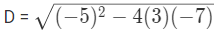
D = 109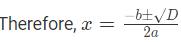
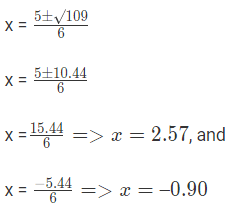
So the two roots are 2.57 and -0.90
Q4: Which method is used to solve quadratic equations that cannot be easily factored or involve complex coefficients?
(a) Factoring
(b) Quadratic Formula
(c) Completing the Square
(d) Estimation
Ans: (b)
The quadratic formula is a universal method used to solve any quadratic equation, regardless of its coefficients or factorability. It provides precise solutions by directly calculating the roots.
Q5: For the quadratic equation 3x² + 6x – 9 = 0, what are the roots?
(a) x = 1
(b) x = -1
(c) x = -3
(d) x = 3
Ans: (c)
Divide the entire equation by 3 to simplify it: x² + 2x – 3 = 0. This equation can be factored as (x – 1)(x + 3) = 0. Setting each factor to zero gives x – 1 = 0 and x + 3 = 0. Solving for “x” in both equations yields x = 1 and x = -3. Therefore, the roots are x = -3 and x = 1.
|
342 videos|310 docs|185 tests
|
FAQs on Tips and Tricks: Quadratic Equations - Quantitative Aptitude for SSC CGL
| 1. What is a quadratic equation? |  |
| 2. How do you solve a quadratic equation using the quadratic formula? |  |
| 3. Are there any shortcuts to solve quadratic equations? |  |
| 4. Can all quadratic equations be solved using shortcuts? |  |
| 5. What are some tips for solving quadratic equations efficiently? |  |
















