Introduction: Routes & Network | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
Introduction
- Recent trends in MBA entrance and aptitude exams indicate a frequent inclusion of questions related to routes and network diagrams.
- It is crucial to grasp these question types and develop effective problem-solving skills within this context.
- Typically, questions on routes and network diagrams revolve around travel or transport scenarios involving multiple nodes.
- The scenarios often depict a journey between two specific nodes, with several intermediate nodes forming a network.
- These questions require a systematic understanding of the relationships and connections between the nodes within the network.
- Problem-solving in this context involves navigating the network to determine optimal routes, distances, or other relevant information.
- Familiarity with these question types is essential for success in MBA entrance exams, as they assess the candidate's ability to analyze and strategize within complex network scenarios.

What are Routes and Networks?
- Examining the logic behind the number of routes in a diagram is essential for problem-solving in scenarios involving travel between specific points.
- Consider a given figure illustrating various routes between points A and G, and the task is to determine the total number of routes available.
- The objective is to navigate through the network of routes, considering the paths and connections between the starting point (A) and the destination (G).
- Understanding the possible combinations and variations in the routes is crucial for accurately counting the total number of routes available.
- Analyzing the given diagram involves assessing the branching points, intersections, and alternative paths that contribute to the overall network of routes.
- The logic behind determining the number of routes requires considering all possible ways to traverse from point A to G, taking into account the various paths and nodes in the network.
- Developing a systematic approach to count the routes ensures a comprehensive understanding of the travel possibilities within the given diagram.
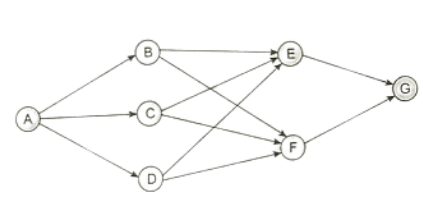
- To count the number of routes efficiently, consider the example where you need to travel from node A to node G through various routes: ABEG, ABFG, ACEG, ACFG, ADEG, and ADFG.
- Adopt the concept of stages for nodes: Node A is Stage 0; Nodes B, C, and D are Stage 1; Nodes E and F are Stage 2, and Node G is Stage 3.
- The movement from one stage to the next determines the number of routes. Going from Stage 0 to Stage 1 (A to B/C/D) involves 3 routes.
- Moving from Stage 1 to Stage 2 has 2 routes, as there are symmetrical options for each node in Stage 1. This results in 2 routes from B, 2 from C, and 2 from D.
- Transitioning from Stage 2 to Stage 3 offers 1 route, as there is only one way to move forward from E to G or from F to G.
- Combining the stages, the overall journey consists of: Stage 0 - Stage 1 - Stage 2 - Stage 3, resulting in 3 × 2 = 6 ways.
- In the case of asymmetry, such as if the route from B to E is closed, divide Stage 1 into Stage 1A (symmetrical nodes C/D) and Stage 1B (asymmetrical node B).
- Journeys can then be calculated as follows:
- Stage 0 - Stage 1A - Stage 2 - Stage 3 = 2 × 2 = 4 ways
- Stage 0 - Stage 1B - Stage 2 - Stage 3 = 1 × 1 = 1 way (since B to E is closed).
- The total number of ways to go from A to G in this scenario is 5.
- Understanding this logic allows for handling asymmetry in route networks effectively.
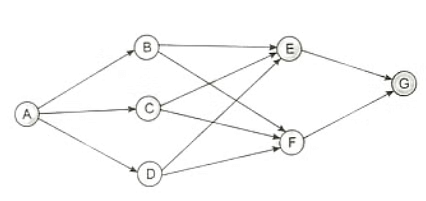
Examine the given figure, where nodes C and D are symmetrical, offering the same number of routes going forward. It is crucial not to disrupt symmetrical thinking through A-C or A-D.
Identify nodes B, E as asymmetrical. To handle this asymmetry, divide the stages into:
Stage 0 (A): Starting point.
Stage 1A (C/D): Symmetrical nodes.
Stage 1B (B): Asymmetrical node.
Stage 1C (E): Asymmetrical node.
Stage 2: Intermediate stage.
Stage 3 (G): Destination.
Consider the routes from A to G through the divided stages:
Stage 0 - Stage 1A - Stage 2 - Stage 3: Symmetrical nodes C/D provide 2 routes each, resulting in 2 × 2 = 4 ways.
Stage 0 - Stage 1B - Stage 2 - Stage 3: Asymmetrical node B offers 1 route.
Stage 0 - Stage 1C - Stage 2 - Stage 3: Asymmetrical node E offers 1 route.
Calculate the total number of ways to go from A to G, factoring in asymmetry: 4 (Stage 1A) + 1 (Stage 1B) + 1 (Stage 1C) = 6 ways.
Understanding and adapting to asymmetry allows for accurate calculation of route networks in complex scenarios.
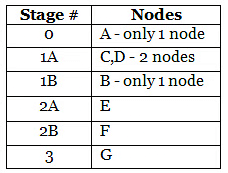
Consider alternate route structures in the given scenario:
Route 1: 0-1A-2A-3
Route 2: 0-1A-2B-3
Route 3: 0-1B-2A-3
Route 4: 0-1B-2B-3.
The following table will clarify the thinking required to count these.

Analyze the routes based on the division of stages:
Route 1 (0-1A-2A-3): Symmetrical nodes C/D in Stage 1A provide 2 routes each, resulting in 2 × 2 = 4 ways.
Route 2 (0-1A-2B-3): Asymmetrical node B in Stage 1B offers 1 route.
Route 3 (0-1B-2A-3): Asymmetrical node B in Stage 1B provides 1 route.
Route 4 (0-1B-2B-3): Asymmetrical node E in Stage 1C offers 1 route.
Calculate the total number of ways considering alternate route structures: 4 (Route 1) + 1 (Route 2) + 1 (Route 3) + 1 (Route 4) = 7 ways.
Utilizing a structured table facilitates clear thinking and accurate counting of alternate routes in a network diagram.
When subdividing route structures, consider the following possibilities based on the given scenario:
Route 1 (0-1A-2A-3): Symmetrical nodes C/D in Stage 1A provide 2 routes each, resulting in 2 × 2 = 4 ways.
Route 2 (0-1A-2A-2B-3): Subdivide Stage 2A into 2A1 and 2A2. Symmetrical nodes C/D in 2A1 offer 2 routes each, resulting in 2 × 2 = 4 ways. Asymmetrical node B in 2A2 provides 1 route. Combine the results for a total of 5 ways.
Route 3 (0-1A-2B-3): Asymmetrical node B in Stage 1B offers 1 route.
Route 4 (0-1B-2A-3): Asymmetrical node B in Stage 1B provides 1 route.
Route 5 (0-1B-2A-2B-3): Subdivide Stage 2A into 2A1 and 2A2. Asymmetrical node B in 2A1 offers 1 route. Asymmetrical node E in 2A2 provides 1 route. Combine the results for a total of 2 ways.
Route 6 (0-1B-1A-2A-3): Subdivide Stage 1B into 1B1 and 1B2. Symmetrical nodes C/D in 1B1 provide 2 routes each, resulting in 2 × 2 = 4 ways. Combine the results for a total of 4 ways.
Route 7 (0-1B-1A-2A-2B-3): Subdivide Stage 2A into 2A1 and 2A2. Symmetrical nodes C/D in 2A1 offer 2 routes each, resulting in 2 × 2 = 4 ways. Asymmetrical node B in 2A2 provides 1 route. Combine the results for a total of 5 ways.
The structured approach allows for the proper counting of routes, and subdividing is used judiciously only when required to avoid confusion.
Additional data about time taken, capacity, or cost for routes may be present in some questions, but the ability to count routes remains crucial for solving problems related to network diagrams.
Solved examples provide insights into various patterns of questions on routes and network diagrams. Practice using the exercise with a comprehensive question bank, and refer to past years' CAT question papers for more examples.
Solved Examples
Illustration 1
Directions for Questions 1 to 3: Answer these questions based on the pipeline diagram below.
The following sketch shows the pipelines carrying material from one location to another. Each location has a demand for material. The demand at Tumkar is 400, at Bangalore is 400, at Kolar is 700 and at Mysore is 200. Each arrow indicates the direction of material flow through the pipeline. The flow from Tumkar to Bangalore is 300. The quantity of material flow is such that the demands at all these locations are exactly met. The capacity of each pipeline is 1000.
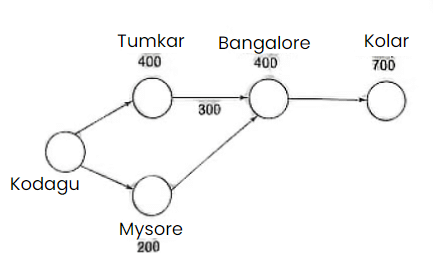
Q1: What is the free capacity available in the Kodagu-Mysore pipeline?
(a) 300
(b) 200
(c) 100
(d) 0
Q2: What is the free capacity available from Kodagu to Tumkar?
(b) 100
(a) 0
(c) 200
(d) 300
Q3: The quantity moved from Kodagu to Mysore is:
(b) 800
(a) 200
(c) 700
(d) 1000
Solution: Since 700 is required at Kolar, the requirement at Bangalore must be 1100, which has to be supplied from the two pipelines coming into Bangalore.
It is clear that since Tumkar to Bangalore is only 300, the Mysore-Bangalore pipeline should carry 800. Hence, Kodagu-Mysore should have 1000.
1. There is no free capacity in the Kodagu Mysore pipeline. Option (d) is correct.
2. Kodagu-Tumkar flow should be 700 and hence, the free capacity is
3. 1000. Option (d) is correct.
Illustration 2
Direction: Seventy percent of the employees in ENY office have IPods, 75 percent have Apple watch, 80 percent have Air purifiers and 85 percent have TV. At least what percentage of employees has all four gadgets?
(a) 15
(b) 5
(c) 10
(d) Cannot be determined
Solution: The least percentage of people with all 4 gadgets would happen if all the employees who are not having any one of the four objects is mutually exclusive.
Thus, 100 - 30 - 25 - 20 - 15 = 10.
Option (c) is correct.
Illustration 3
Directions for Questions: Answer the questions on the basis of the following information.
Shown below is the layout of major streets in a city.
Two days (Thursday and Friday) are left for campaigning before a major election, and the city administration has received requests from five political parties to take out their processions along the following routes.
- All India Party: A-C-D-E
- BMP: A-B-D-E
- Bolo Bharat: A-B-C-E
- Manki Baat: B-C-E
- PCM: A-C-D
Street B-D cannot be used for a political procession on Thursday due to a religious procession. The district administration has a policy of not allowing more than one precession to pass along the same street on the same day. However, the administration must allow all parties to take out their processions during these two days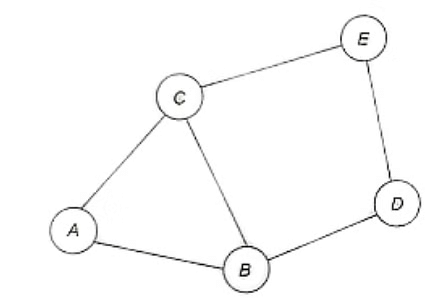
Q4: All India Party procession can be allowed:
(a) Only on Thursday
(b) Only on Friday
(c) On either day
(d) Only if the religious procession is cancelled.
Solution: The BJP procession must be allowed on Friday - since the BJP procession uses BD and that road is not free for a political procession on Thursday due to the religious procession. Also, we can see that the BJP and All India Party procession cannot be on the same day (since they have a common street usage viz: street DE). Thus, if BJP is going on Friday, All India Party cannot be allowed on Friday. Thus, the All India Party procession would only be allowed on Thursday. Option (a) is correct.
Q5: Which of the following is not true?
(a) All India Party and Bolo Bharat can take out their processions on the same day.
(b) The PCM procession cannot be allowed on Thursday.
(c) The BJP procession can only take place on Friday.
(d) All India Party and Manki Baat can take out their processions on the same day.
Solution: From the previous question, we know that BJP is Friday and All India Party is Thursday. Since street AD is used by both BJP and Bolo Bharat, Bolo Bharat must also be on Thursday. The Manki Baat and Bolo Bharat use the same street CE.
So, they should be on different days and hence, the Manki Baat is on Friday. Also, the PCM should be on Friday as it cannot be on the same day as the All India Party procession. Looking through the options, we have to spot the option that is false. Option (a), (b) and (c) can be seen to be true. Only option (d) is not true as we can see that the All India Party and Manki Baat procession cannot be on the same day. Hence, option(d) is correct.
|
77 videos|180 docs|96 tests
|
FAQs on Introduction: Routes & Network - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What is the definition of routes and networks? |  |
| 2. How are routes determined in a network? |  |
| 3. What are the different types of network routes? |  |
| 4. Can a network have multiple routes to the same destination? |  |
| 5. How does a network choose the best route for data packets? |  |
















