Tips and Tricks: Geometric Progressions | Quantitative Aptitude for SSC CGL PDF Download
Geometric Progression Tricks
In a geometric progression (GP), each successive term is obtained by multiplying a constant number with its preceding term. If we divide any succeeding term by its preceding term, we obtain a value equal to the common ratio.

Geometric Progression Tips and Tricks and Shortcuts
- Three non-zero terms a, b, c are in GP if and only if b2 = ac.
- In a GP, three consecutive terms can be taken as a/r, a, ar….
- If a, b and c are three quantities in GP, then their reciprocals (b/a), (c/b), and (c/a) are also in GP.
- If we multiply or divide each term of the GP by a non-zero quantity, then resulting sequence remains a GP with the same common ratio.
Type 1: Find nth term of the series
Example 1: Find 11th term in the series 2,4,8,16 …
(a) 2042
(b) 2200
(c) 1024
(d) 2048
Ans: (d)
We know that,
an = arn-1
where
r(common ratio) = 4/2 = 2
a1= first term = 2
an-1 = the term before the nth term,
n = number of terms
In the given series,
r (common ratio) = 4/2 = 2
Therefore, 11th term = a11
a11 = 2 x 211-1
a11 = 2 x 210
a11 = 2 x 1024
a11 = 2048
Example 2: Find last term in the series if there are 7 term in this series 3,15,75,375 …
(a) 46875
(b) 44875
(c) 42875
(d) 40875
Ans: (a)
We know that,
an = arn-1
where
r(common ratio) = 15/3 = 5
a1= first term = 3
an-1= the term before the nth term,
n = number of terms
In the given series,
r (common ratio) = 15/3 = 5
Therefore, 7th term = a7
a7 = 3 x 57-1
a7 = 46875
Type 2: Find number of terms in the series
(a) 6
(b) 7
(c) 9
(d) 8
Ans: (c)
We know that,
In the given series,
a1 = 6,
a2 = 12,
r = 12/6 = 2
an = 1536
an = arn-1
1536 = 6 x 2n-1 (divide both side by 6)
256 = 2n-1
28 = 2n-1
8 = n – 1
n = 9
Therefore, there are 9 terms in the series.
(a) 10
(b) 7
(c) 9
(d) 6
Ans: (d)
We know that,
In the given series,
a1 = 10,
a2 = 40,
r = 40/10 = 4
an = 10240
an = arn-1
10240 = 10 x 4n-1 (divide both side by 10)
1024 = 4n-1
45 = 4n-1
5 = n – 1
n = 6
Therefore, there are 6 terms in the series.
Type 3: Related to sum of first ‘n’ terms of the Geometric series
Example 1: How many terms of the series 1 + 3 + 9 +….sum to 121
(a) 18
(b)19
(c) 13
(d) 5
Ans: (d)
We know that,
In the given series,
a = 1,
r = 3/1 = 3,
Sn = 121
242 = (3n – 1)
243 = 3n
35 = 3n
n = 5
Example 2: Find Sum of given Geometric Series upto 9th term 7,14,28,56……
(a) 3177
(b) 3577
(c) 1377
(d) 5377
Ans: (b)
We know that,
In the given series,
a = 7,
r = 14/7 = 2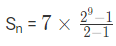
= 3577
Type 4: Find the Geometric Mean (GM) of the series.
Example 1: What is the geometric mean of 2, 3, and 6?
(a) 4.5
(b) 6.5
(c) 3.30
(d) 6.4
Ans: (c)
We know that,
GM = (abc)1/3
Therefore, there Geometric Mean (GM) = (2 x 3 x 6)1/3
= 3.30
Example 2: What is the geometric mean of 36 and 9?
(a) 24
(b) 16
(c) 18
(d) 14
Ans: (c)
We know that,
GM = (ab)1/2
Therefore, there Geometric Mean (GM) = (36 x 9)1/2
= 18
|
314 videos|170 docs|185 tests
|
FAQs on Tips and Tricks: Geometric Progressions - Quantitative Aptitude for SSC CGL
| 1. What is a geometric progression? |  |
| 2. How do you find the nth term of a geometric progression? |  |
| 3. Can the common ratio in a geometric progression be negative? |  |
| 4. How can geometric progressions be used in real-life situations? |  |
| 5. What is the sum of a geometric progression? |  |
|
314 videos|170 docs|185 tests
|

|
Explore Courses for SSC CGL exam
|

|

















