Solved Examples: Geometric Progressions | Quantitative Aptitude for SSC CGL PDF Download
Definition
A geometric progression is a type of sequence characterized by an ordered and infinite collection of real numbers, where each term is obtained by multiplying its preceding term by a constant value.
General form of Geometric Progression
a, ar, ar2, ar3, ……..
where,
The first term is denoted as = a
The common ratio is denoted as = r
Types of Geometric Progression
Geometric progression can be classified based on the number of terms in the sequence.
- Finite Geometric Progression: A finite geometric progression is a sequence of numbers that has a fixed number of terms. The general form of a finite geometric progression is:
a, ar, ar2, ar3, ar4, …, ar(n-1)
For example: 2, 4, 8,16 - Infinite Geometric Progression: An infinite geometric progression is a sequence of numbers that goes on forever. The general form of an infinite geometric progression is :
a, ar, ar2, ar3, ar4, …,
For example: 2, 4, 8, …………
Geometric Progression finds application in physics, engineering, biology, economics, computer science, queueing theory, and finance. This underscores the importance of understanding Geometric Progression questions and answers.
Examples
Example 1: How do you find S7 for the geometric series 1 + 9 + 81 + 729 +…?
(a) 6,94,765
(b) 5,97,871
(c) 2,44,406
(d) None of the above
Ans: (b)
First term a = 1 and r = 9.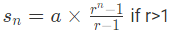
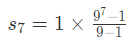
= 5,97,871
Example 2: Find the sum of the geometric series 8, − 4, + 2, − 1,. . . where there are 7 terms in the series.
(a) 5.37
(b) 5.50
(c) 6.34
(d) None of the above
Ans: (a)
For this series, we have a = 8, r = -1/2 and n = 7
Thus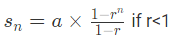
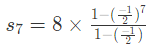
S7 =5.37.
Example 3: If Product of 3 successive terms of Geometric Progression is 8 then mid of those 3 successive terms will be
(a) 2
(b) 12
(c) 4
(d)13
Ans: (a)
Let x/r , x, xr be three terms ,then 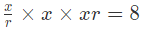
x = 2
Example 4: What is the sum of below given infinite g.p.?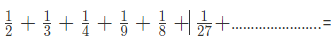
(a) 1/2
(b) 2/3
(c) 2/5
(d) 3/2
Ans: (d)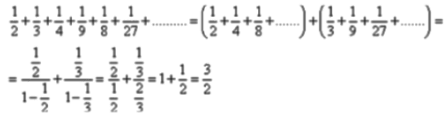
Example 5: How do you find the sum of the first 6 terms of the geometric series: 6+ 36 + 216…?
(a) 33454
(b) 55986
(c) 43659
(d) 76463
Ans: (b)
Common ratio = 6 and First term = 6
As per the formula: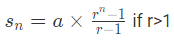
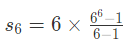
= 55986
Example 6: Find the sum of the geometric series 3 + 9 + 27 + 81 + . . . where there are 5 terms in the series.
(a) 363
(b) 362
(c) 242
(d) 243
Ans: (a)
For this series, we have a = 3, r = 3 and n = 5.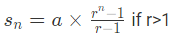

Example 7: How many terms are there in the geometric progression 4, 8, 16, . . ., 512?
(a) 5
(b) 6
(c) 7
(d) 8
Ans: (d)
Here a = 4 and r = 2. nth term = 512. But the formula for the nth term is arn−1
So
512 = 4 × 2n−1
128 = 2n−1
27 = 2n−1
7 = n − 1
n = 8.
Example 8: How do you find S₁₀ for the geometric series 1 + 5 + 25 + 125 +…?
(a) 25,00,000
(b) 23,87,463
(c) 24,41,406
(d) None of the above
Ans: (c)
As we know first term a=1 and r=5.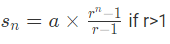
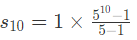
= 24,41,406
Example 9: How do you find s17 for the geometric series 5 + 15 + 45 + 135 + …?
(a) 32,28,50,405
(b) 12,91,40,631
(c) 34,2154,214
(d) None of the above
Ans: (a)
As we know first term a=5 and r=3.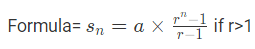
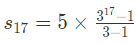
=32,28,50,405
Example 10: Find out the sum of the next infinite geometric series, if it exists? 3 + 2.25 + 1.6875 + 1.265625+…?
(a) 10
(b) 11
(c) 12
(d) 13
Ans: (c)
Here a = 3
r = 0.75
Since |r|<1
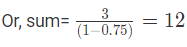
|
314 videos|170 docs|185 tests
|
FAQs on Solved Examples: Geometric Progressions - Quantitative Aptitude for SSC CGL
| 1. What is a geometric progression? |  |
| 2. How is a geometric progression different from an arithmetic progression? |  |
| 3. Can a geometric progression have a negative common ratio? |  |
| 4. What is the formula to find the nth term of a geometric progression? |  |
| 5. How can geometric progressions be applied in real-life situations? |  |
|
314 videos|170 docs|185 tests
|

|
Explore Courses for SSC CGL exam
|

|

















