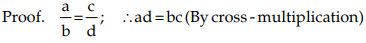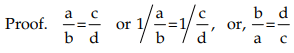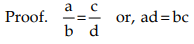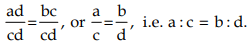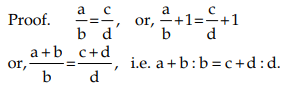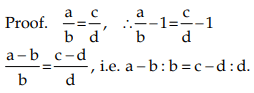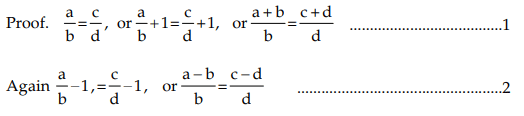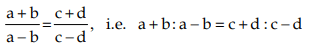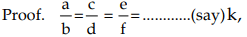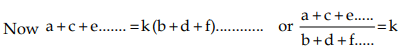Proportion Chapter Notes | Quantitative Aptitude for CA Foundation PDF Download
Overview

Proportions
If a man's income increases in a specified ratio and the amount of increase is known, we can determine his new income using proportion principles. Similarly, if two men's ages are in a given ratio and the age of one man is known, we can calculate the age of the other man through proportion. An equality of two ratios is defined as a proportion. Four quantities a, b, c, and d are in proportion if a : b = c : d (also expressed as a : b :: c : d), meaning a/b = c/d or ad = bc. The quantities a, b, c, and d are referred to as the terms of the proportion, with a, b, c, and d identified as the first, second, third, and fourth terms, respectively. The first and fourth terms are known as extremes (or extreme terms), while the second and third terms are called means (or middle terms).If a : b = c : d then d is called fourth proportional.
If a : b = c : d are in proportion then a/b = c/d i.e. ad = bc
i.e. product of extremes = product of means.
This is called cross product rule.
Three quantities a, b, c of the same kind (in same units) are said to be in continuous proportion
if a : b = b : c i.e. a/b = b/c i.e. b2 = ac
If a, b, c are in continuous proportion, then the middle term b is called the mean proportional between a and c, a is the first proportional and c is the third proportional.
Thus, if b is mean proportional between a and c, then b2 = ac i.e. b = √ac.
When three or more numbers are so related that the ratio of the first to the second, the ratio of the second to the third, third to the fourth etc. are all equal, the numbers are said to be in continued proportion. We write it as
x/y = y/z = z/w = w/p = p/q = ................................................. when
x, y, z, w, p and q are in continued proportion. If a ratio is equal to the reciprocal of the other, then either of them is in inverse (or reciprocal) proportion of the other. For example 5/4 is in inverse proportion of 4/5 and vice-versa.
Note:
In a ratio a : b, both elements must be of the same type, whereas in a proportion a : b = c : d, the four elements do not all need to be of the same type. The first two elements should be of one kind, and the last two should be of another kind.
Applications:
Illustration I: ₹ 6 : ₹ 8 = 12 toffees : 16 toffees are in a proportion.
Here 1st two quantities are of same kind and last two are of same kind.
Example 1: The numbers 2.4, 3.2, 1.5, 2 are in proportion because these numbers satisfy the property the product of extremes = product of means.
Here 2.4 × 2 = 4.8 and 3.2 × 1.5 = 4.8
Example 2: Find the value of x if 10/3 : x : : 5/2 : 5/4.
Sol: 10/3 : x = 5/2 : 5/4 Using cross product rule, x × 5/2 = (10/3) × 5/4 Or, x = (10/3) × (5/4) × (2/5) = 5/3
Example 3: Find the fourth proportional to 2/3, 3/7, 4.
Sol: If the fourth proportional be x, then 2/3, 3/7, 4, x are in proportion. Using cross product rule, (2/3) × x = (3 × 4)/7 or, x = (3 × 4 × 3)/(7 × 2) = 18/7.
Example 4: Find the third proportion to 2.4 kg, 9.6 kg.
Sol: Let the third proportion to 2.4 kg, 9.6 kg be x kg.
Then 2.4 kg, 9.6 kg and x kg are in continued proportion since b2 = ac
So, 2.4/9.6 = 9.6/x or, x = (9.6 × 9.6)/2.4 = 38.4
Hence the third proportional is 38.4 kg.
Example 5: Find the mean proportion between 1.25 and 1.8.
Sol: Mean proportion between 1.25 and 1.8 is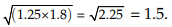
Properties of Proportion
- If a : b = c : d, then ad = bc

- If a : b = c : d, then b : a = d : c (Invertendo)

Hence, b : a = d : c. - If a : b = c : d, then a : c = b : d (Alternendo)

Dividing both sides by cd, we get
- If a : b = c : d, then a + b : b = c + d : d (Componendo)

If a : b = c : d, then a – b : b = c – d : d (Dividendo)

If a : b = c : d, then a + b : a – b = c + d : c – d (Componendo and Dividendo)

Dividing (1) by (2) we get
If a : b = c : d = e : f = ………………..….., then each of these ratios (Addendo) is equal (a + c + e + ……..) : (b + d + f + …….)

∴ a = bk, c = dk, e = fk, .............
Hence, (a + c + e + ……..) : (b + d + f + …….) is equal to each ratioSubtrahendo: If a : b = c : d = e : f = ………………..….., then each of these ratios is equal
(a – c – e – ……..) : (b – d – f – …….)
Example 1: If a : b = c : d = 2.5 : 1.5, what are the values of ad : bc and a + c : b + d?
Sol: We have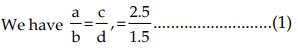
From (1) ad = bc, or, ad/bc = 1 , i.e. ad : bc = 1 : 1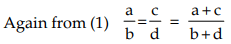 (By addendo property)
(By addendo property)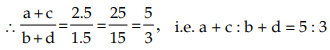
Hence, the values of ad : bc and a + c : b + d are 1 : 1 and 5 : 3 respectively.
Example 2: 
Sol: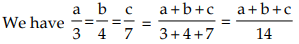 (By addendo property)
(By addendo property)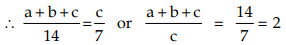
Example 3: A dealer mixes tea costing ₹ 6.92 per kg. with tea costing ₹ 7.77 per kg and sells the mixture at ₹ 8.80 per kg and earns a profit of 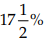 on his sale price. In what proportion does he mix them?
on his sale price. In what proportion does he mix them?
Sol: Let us first find the cost price (C.P.) of the mixture. If S.P. is ₹ 100, profit is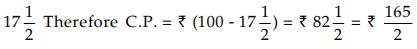
If S.P. is ₹ 8.80, C.P. is (165 × 8.80)/(2 × 100) = ₹ 7.26
C.P. of the mixture per kg = ₹ 7.26
2nd difference = Profit by selling 1 kg. of 2nd kind @ ₹ 7.26
= ₹ 7.77 – ₹ 7.26 = 51 Paise
1st difference = ₹ 7.26 – ₹ 6.92 = 34 Paise
We have to mix the two kinds in such a ratio that the amount of profit in the first case must balance the amount of loss in the second case.
Hence, the required ratio = (2nd diff) : (1st diff.) = 51 : 34 = 3 : 2.
|
114 videos|164 docs|98 tests
|
FAQs on Proportion Chapter Notes - Quantitative Aptitude for CA Foundation
| 1. What are the basic concepts of proportions in mathematics? |  |
| 2. How can I solve problems involving proportions in the CA Foundation exam? |  |
| 3. What are some common types of proportion problems I should prepare for in the CA Foundation exam? |  |
| 4. Are there any shortcuts or tips for solving proportion questions quickly? |  |
| 5. How important is understanding proportions for the CA Foundation exam overall? |  |
|
114 videos|164 docs|98 tests
|

|
Explore Courses for CA Foundation exam
|

|