ICAI Notes- Proportion | Quantitative Aptitude for CA Foundation PDF Download

Overview

Proportions

If the income of a man is increased in the given ratio and if the increase in his income is given then to find out his new income, in a Proportion problem is used. Again if the ages of two men are in the given ratio and if the age of one man is given, we can find out the age of the another man by Proportion. An equality of two ratios is called a proportion. Four quantities a, b, c, d are said to be in proportion if a : b = c : d (also written as a : b :: c : d) i.e. if a/b = c/d i.e. if ad = bc. The quantities a, b, c, d are called terms of the proportion; a, b, c and d are called its first, second, third and fourth terms respectively. First and fourth terms are called extremes (or extreme terms). Second and third terms are called means (or middle terms).
If a : b = c : d then d is called fourth proportional.
If a : b = c : d are in proportion then a/b = c/d i.e. ad = bc
i.e. product of extremes = product of means.
This is called cross product rule.
Three quantities a, b, c of the same kind (in same units) are said to be in continuous proportion
if a : b = b : c i.e. a/b = b/c i.e. b² = ac
If a, b, c are in continuous proportion, then the middle term b is called the mean proportional between a and c, a is the first proportional and c is the third proportional.
Thus, if b is mean proportional between a and c, then b² = ac i.e. b = √ac.

When three or more numbers are so related that the ratio of the first to the second, the ratio of the second to the third, third to the fourth etc. are all equal, the numbers are said to be in continued proportion. We write it as
x/y = y/z = z/w = w/p = p/q = ................................................. when
x, y, z, w, p and q are in continued proportion. If a ratio is equal to the reciprocal of the other, then either of them is in inverse (or reciprocal) proportion of the other. For example 5/4 is in inverse proportion of 4/5 and vice-versa. 

Note: In a ratio a : b, both quantities must be of the same kind while in a proportion a : b = c : d, all the four quantities need not be of the same type. The first two quantities should be of the same kind and last two quantities should be of the same kind. 

Applications:
Illustration I: ₹ 6 : ₹ 8 = 12 toffees : 16 toffees are in a proportion.
Here 1st two quantities are of same kind and last two are of same kind. 

Example 1: The numbers 2.4, 3.2, 1.5, 2 are in proportion because these numbers satisfy the property the product of extremes = product of means.
Here 2.4 × 2 = 4.8 and 3.2 × 1.5 = 4.8 

Example 2: Find the value of x if 10/3 : x : : 5/2 : 5/4.
Sol: 10/3 : x = 5/2 : 5/4 Using cross product rule, x × 5/2 = (10/3) × 5/4 Or, x = (10/3) × (5/4) × (2/5) = 5/3

Example 3: Find the fourth proportional to 2/3, 3/7, 4.
Sol: If the fourth proportional be x, then 2/3, 3/7, 4, x are in proportion. Using cross product rule, (2/3) × x = (3 × 4)/7 or, x = (3 × 4 × 3)/(7 × 2) = 18/7. 

Example 4: Find the third proportion to 2.4 kg, 9.6 kg.
Sol: Let the third proportion to 2.4 kg, 9.6 kg be x kg.
Then 2.4 kg, 9.6 kg and x kg are in continued proportion since b² = ac
So, 2.4/9.6 = 9.6/x or, x = (9.6 × 9.6)/2.4 = 38.4
Hence the third proportional is 38.4 kg.

Example 5: Find the mean proportion between 1.25 and 1.8.
Sol: Mean proportion between 1.25 and 1.8 is

Properties of Proportion

1. If a : b = c : d, then ad = bc
   
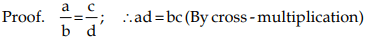
2. If a : b = c : d, then b : a = d : c (Invertendo)
   
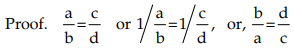
   Hence, b : a = d : c.
3.  If a : b = c : d, then a : c = b : d (Alternendo)
   
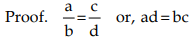
   Dividing both sides by cd, we get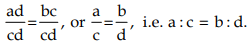
   
4.  If a : b = c : d, then a + b : b = c + d : d (Componendo)
   

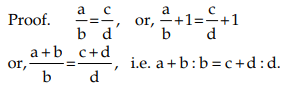
5. If a : b = c : d, then a – b : b = c – d : d (Dividendo)
   

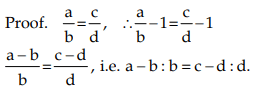
6.  If a : b = c : d, then a + b : a – b = c + d : c – d (Componendo and Dividendo)
   
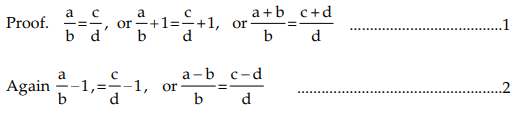
   Dividing (1) by (2) we get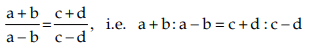
   

7. If a : b = c : d = e : f = ………………..….., then each of these ratios (Addendo) is equal (a + c + e + ……..) : (b + d + f + …….)
   
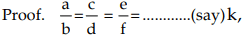
   ∴ a = bk, c = dk, e = fk, .............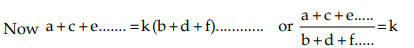
   
   Hence, (a + c + e + ……..) : (b + d + f + …….) is equal to each ratio

8. Subtrahendo: If a : b = c : d = e : f = ………………..….., then each of these ratios is equal
   (a – c – e – ……..) : (b – d – f – …….)

Example 1: If a : b = c : d = 2.5 : 1.5, what are the values of ad : bc and a + c : b + d?
Sol: We have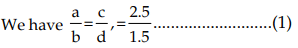

From (1) ad = bc, or, ad/bc = 1 , i.e. ad : bc = 1 : 1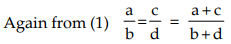
 (By addendo property)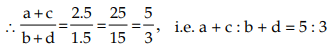

Hence, the values of ad : bc and a + c : b + d are 1 : 1 and 5 : 3 respectively.

Example 2:
Sol: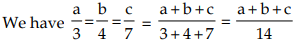
 (By addendo property)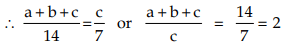

Example 3: A dealer mixes tea costing ₹ 6.92 per kg. with tea costing ₹ 7.77 per kg and sells the mixture at ₹ 8.80 per kg and earns a profit of 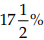 on his sale price. In what proportion does he mix them?
Sol: Let us first find the cost price (C.P.) of the mixture. If S.P. is ₹ 100, profit is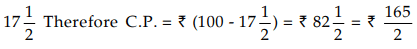

If S.P. is ₹ 8.80, C.P. is (165 × 8.80)/(2 × 100) = ₹ 7.26
 C.P. of the mixture per kg = ₹ 7.26
2nd difference = Profit by selling 1 kg. of 2nd kind @ ₹ 7.26
 = ₹ 7.77 – ₹ 7.26 = 51 Paise
1st difference = ₹ 7.26 – ₹ 6.92 = 34 Paise
We have to mix the two kinds in such a ratio that the amount of profit in the first case must balance the amount of loss in the second case.
Hence, the required ratio = (2nd diff) : (1st diff.) = 51 : 34 = 3 : 2.