Important Derivations: Waves | Physics for SSS 3 PDF Download

Step-By-Step Derivation of Doppler Effect

In order to derive the Doppler effect, there are two situations that needs to considered, and they are:

Moving Source and Stationary Observer Where the Wave Travels with the Source

Where,
c: wave velocity
λs: wavelength of the source
T: time taken by the wave

Where,
v_s: velocity with which source is moving towards a stationary observer
d: distance covered by the source

Moving Observer and a Stationary Source

Where,
f₀: observed frequency
v₀: observer velocity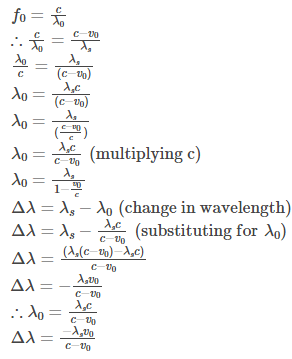

One Dimensional Wave Equation Derivation

The wave equation in classical physics is considered to be an important second-order linear partial differential equation to describe the waves. The wave equation arises in fields like fluid dynamics, electromagnetics, and acoustics. D’Alembert discovered the one-dimensional wave equation in 1746, after ten years Euler discovered the three-dimensional wave equation.

One Dimensional Wave Equation Derivation

Consider the relation between Newton’s law that is applied to the volume ΔV in the direction x:

Where,
F: force acting on the element with volume ΔV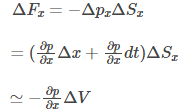


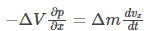
(as dt is small, it is not considered and ΔSx is in x direction so ΔyΔz and from Newton Law.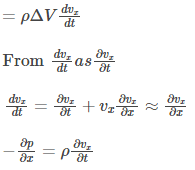

Above equation is known as the equation of motion.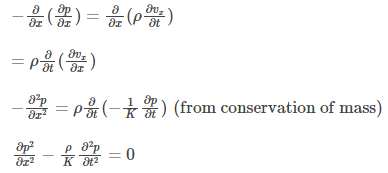

Where,
K: bulk modulus
Rewriting the above equation: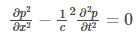

Where,
K: bulk modulus
Rewriting the above equation: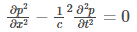

Where,
c: velocity of sound given as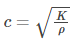

Thus, above is the one-dimensional wave equation derivation.