Overview: Divisibility | Quantitative for GMAT PDF Download
| Table of contents |

|
| Arithmetic Rules |

|
| Rules of Divisibility |

|
| Using Divisibility Rules for Prime Factorization Questions |

|
| Using Divisibility Rules to Determine What Numbers Divide Other Numbers |

|
Integers are ‘whole” numbers, such as 0, 1, 2, and 3, that have no fractional part. Integers can be positive (1, 2, 3...), negative (-1, -2, -3.. .), or the number 0.
Arithmetic Rules
- Most arithmetic operations on integers will always result in an integer. For instance, when you add or subtract integers, like 4 + 5 or (-2) + 1, the answer is always an integer. The same goes for multiplication; if you multiply integers, such as 4 × 5 or (-2) × 3, the result is always an integer.
- However, division is a bit different. Sometimes, when you divide two integers, you get an integer as a result, and sometimes you don't.
- For example, 8 ÷ 2 equals 4, which is an integer, but 2 ÷ 8 results in 0.25, which is not an integer.
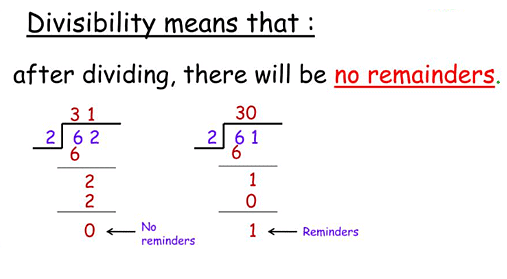
- An integer is said to be divisible by another number if you can divide it by that number and get an integer result (meaning there's no remainder).
 For instance, 21 is divisible by 3 because when you divide 21 by 3, you get an integer (21 ÷ 3 = 7). However, 21 is not divisible by 4 because when you divide 21 by 4, you get a non-integer result (21 ÷ 4 = 5.25).
For instance, 21 is divisible by 3 because when you divide 21 by 3, you get an integer (21 ÷ 3 = 7). However, 21 is not divisible by 4 because when you divide 21 by 4, you get a non-integer result (21 ÷ 4 = 5.25). - In simpler terms, if you can divide a number by another number and get a whole number without any leftover bit, then the first number is divisible by the second. For example, 8 is divisible by 2 because when you divide 8 by 2, you get 4 with no remainder.
- Examples:
8 ÷ 2 equals 4, so 8 is divisible by 2.
2 ÷ 8 equals 0.25, so 2 is not divisible by 8.
(-6) ÷ 2 equals -3, so -6 is divisible by 2.
(-6) ÷ (-4) equals 1.5, so -6 is not divisible by -4.
In essence, divisibility means you can divide one number by another and get a whole number without any leftover bits. If you can do that, the first number is divisible by the second. If there's a leftover bit, then it's not divisible.
Rules of Divisibility
- Divisibility Rules can be helpful in simplifying numbers and prime factorization
- These rules can be helpful in determining whether a number is a multiple of another number.

1. Number Divisible by 0
- No number is divisible by 0.
2. Number Divisible by 2
- A number is divisible by 2 if the ones digit is 0, 2, 4, 6, or 8 – that is, if the units digit is even.
- For example, 30, 42, 54, 66, and 78 are divisible by 2.
3. Number Divisible by 3
- A number is divisible by 3 if the sum of all the digits is divisible by 3.
- For example, 472,071 is divisible by 3 because the sum of its digits (4 + 7 + 2 + 0 + 7 + 1 = 21) is divisible by 3.
4. Number Divisible by 4
- If the last two digits of a number are divisible by 4, then the number is divisible by 4.
- For example, the last two digits of 244 are 44, which is divisible by 4. Students sometimes fail to see that a number that ends in 00 is divisible by 4. Just remember that all multiples of 100 are divisible by 4, since 100 = 25 x 4.
5. Number Divisible by 5
- A number is divisible by 5 if the last (ones) digit is 0 or 5.
- For example, the numbers 55 and 70 are divisible by 5.
6. Number Divisible by 6
- A number is divisible by 6 if the number in question is an even number whose digits sum to a multiple of 3 (and therefore the number is divisible by both 2 and 3, the factors of 6).
- For example, 18 is an even number, and its digits, 1 and 8, sum to 9, a multiple of 3.
7. Number Divisible by 7
- There are tricky formulas for this, but their logic is complicated. So, if you are asked whether a number is divisible by 7, just do the division.
8. Number Divisible by 8
- If the number is even, divide the last three digits by 8. If there is no remainder, then the original number is divisible by 8.
- For example, the number 1,160 is divisible by 8 because 160/8 = 20, which is an integer. Students often fail to see that if a number ends in 000, the number is divisible by 8. Just remember that all multiples of 1,000 are divisible by 8 because 1000 = 125 x 8.
9. Number Divisible by 9
- A number is divisible by 9 if the sum of all the digits is divisible by 9.
- For example, 479,655 is divisible by 9 because the sum of the digits (4 + 7 + 9 + 6 + 5 + 5 = 36) is divisible by 9.
10. Number Divisible by 10
- If the ones digit is 0, then the number is divisible by 10.
- For example, 10, 80, 90, 100, 1,120, and 10,000 are all divisible by 10.
11. Number Divisible by 11
- A number is divisible by 11 if the sum of the odd-numbered place digits minus the sum of the even-numbered place digits is divisible by 11.
- The odd-numbered place digits are the 1st, 3rd, 5th, and so on digits to the left of the decimal point.
- Hence, they are the ones, hundreds, ten-thousands, and so on digits. Similarly, the even-numbered place digits are the 2nd, 4th, 6th, and so on digits to the left of the decimal point.
- Hence, they are the tens, thousands, hundred-thousands, and so on digits.
- For example, 253 is divisible by 11 because (2 + 3) – 5 = 0, which is divisible by 11 (remember, 0 is divisible by any number except itself). Likewise, 2,915 is divisible by 11 because (9 + 5) – (2 + 1) = 11, which is divisible by 11.
12. Number Divisible by 12
- If a number is divisible by both 3 and 4, the number is also divisible by 12.
- For example, since 24 is divisible by both 3 and 4, 24 is also divisible by 12.
Now that we’ve reviewed the divisibility rules, let’s discuss two scenarios in which the divisibility rules could be helpful.
Using Divisibility Rules for Prime Factorization Questions
- Let’s say, for example, that we were given the number 288 and needed to break 288 into prime factors.
- While we quickly see that 288 is an even number and thus divisible by 2, in order to most efficiently break 288 into prime factors, it is helpful to find a number larger than 2 (if applicable) that divides 288.
- Since the digits of 288 add up to 2 + 8 + 8 = 18, we see that 288 is divisible by 9, so we can begin the prime factorization by dividing 288 by 9. 288 = 9 * 32 = 3 * 3 * 8 * 4 = 3^2 * 2^3 * 2^2 = 3^2 * 2^5
- Although what we did may seem insignificant, beginning your prime factorization by dividing by a large number allows you to take fewer steps when breaking numbers into prime factors, thus saving you time.
- If you are able to save even 10 seconds on every question, you will save 31 * 10 = 310 seconds, or almost 5 minutes, on the Quant section.
Next, let’s discuss using divisibility rules when answering GMAT questions that directly involve divisibility.
Using Divisibility Rules to Determine What Numbers Divide Other Numbers
We just discussed how we can use divisibility rules in questions that don’t directly ask about divisibility, but, of course, these rules also can be helpful in answering divisibility questions. Consider the following example:
Q. If T = 213, 425, 212, then T + 2 must be divisible by which of the following?
I. 3
II. 6
III. 12
(a) I only
(b) I and II
(c) I and III
(d) II and III
(e) I, II, and III
Ans: (b)
Explanation: T + 2 = 213, 425, 214. It would be time-prohibitive to divide each of the answer choices into T + 2. Instead, we’ll use the rules of divisibility. Because T + 2 ends in 4, which is an even number, it’s divisible by 2. In addition, the digits of T + 2 sum as follows: 2 + 1 + 3 + 4 + 2 + 5+ 2 + 1 + 4 = 24, which is a multiple of 3; thus, T + 2 is divisible by 3. So, we know that T + 2 is divisible by 2 and by 3. This also means that T + 2 is divisible by 6 because the prime factorization of 6 is 3 × 2. Thus, T + 2 is divisible by 3 and by 6. Finally, we’ve learned that if a number is divisible by 3 and 4, it is also divisible by 12. Since we know that T + 2 is divisible by 3, we only need to determine whether it is also divisible by 4. We divide 14, the last two digits of T + 2, by 4. Since 14 is not divisible by 4, T + 2 is not divisible by 4, and thus is not divisible by 12.
|
115 videos|106 docs|113 tests
|
FAQs on Overview: Divisibility - Quantitative for GMAT
| 1. What are the arithmetic rules of divisibility? |  |
| 2. What is the rule of divisibility for 2? |  |
| 3. How can I determine if a number is divisible by 3? |  |
| 4. What is the rule of divisibility for 5? |  |
| 5. How can I determine if a number is divisible by 9? |  |

|
Explore Courses for GMAT exam
|

|
 For instance, 21 is divisible by 3 because when you divide 21 by 3, you get an integer (21 ÷ 3 = 7). However, 21 is not divisible by 4 because when you divide 21 by 4, you get a non-integer result (21 ÷ 4 = 5.25).
For instance, 21 is divisible by 3 because when you divide 21 by 3, you get an integer (21 ÷ 3 = 7). However, 21 is not divisible by 4 because when you divide 21 by 4, you get a non-integer result (21 ÷ 4 = 5.25).
















