Important Derivations: Kinetic Theory of Gases | Physics for Grade 12 PDF Download
What Is Kinetic Theory of Gases?
The kinetic theory of gases describes a gas as a large number of submicroscopic particles such as atoms and molecules, all of which are in random and constant motion. The randomness arises from the particles’ collisions with each other and with the walls of the container.
Derivation of Kinetic Gas Equation
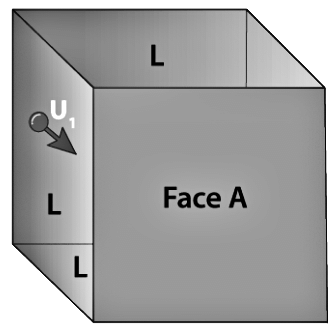
Consider a cubical container of length ‘l ’ filled with gas molecules each having mass ‘m’ and let N be the total number of gas molecules in the container. Due to the influence of temperature, the gas molecules move in random directions with a velocity ‘v.’
The pressure of the gas molecules is the force exerted by the gas molecule per unit area of the wall of the container and is given by the equation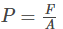
Let us consider a gas molecule moving in the x-direction towards face A. The molecule hits the wall with a velocity Vx and rebounds back with the same velocity Vx, and will experience a change of momentum which is equal to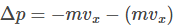
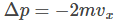
For a total of N number of gas molecules in the container, the total change in momentum is given by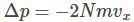
The force is given by the equation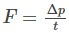
Therefore,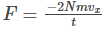
Gas molecules will hit the wall A and will travel back across the box, collide with the opposite face and hit face A again after a time t which is given by the equation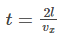
Substituting the value of t in the force equation, we get the force on the molecules as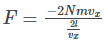
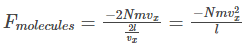
Therefore, the force exerted on the wall is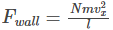
Now, the pressure P is given by the equation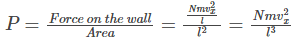
Hence,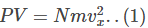
Since vx, vy and vz are independent speeds in three directions and if we consider the gas molecules in bulk, then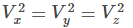
We know, volume V = l3
Hence,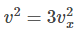
Substituting the above condition in eq (1), we get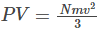
Therefore,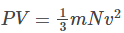
This equation above is known as the kinetic theory equation.
The velocity v in the kinetic gas equation is known as the root-mean-square velocity and is given by the equation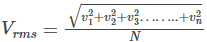
We use this equation to calculate the root-mean-square velocity of gas molecules at any given temperature and pressure.
Maxwell Boltzmann Distribution Derivation
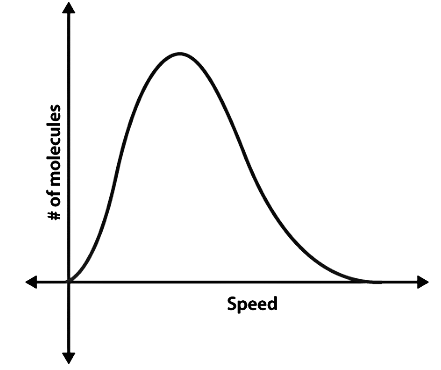
Not all the air molecules surrounding us travel at the same speed. Some air molecules travel faster, some move at moderate speeds, and some air molecules will hardly move at all. Hence, instead of asking about the speed of any particular gas molecule, we ask about the distribution of speed in a gas at a certain temperature. James Maxwell and Ludwig Boltzmann came up with a theory to show how the speeds of the molecules are distributed for an ideal gas. The distribution is often represented using the following graph.
Maxwell Boltzmann Distribution
 In the next section, let us look at the Maxwell Boltzmann distribution derivation.
In the next section, let us look at the Maxwell Boltzmann distribution derivation.Derivation of Maxwell-Boltzmann Distribution
Consider a system that consists of identical yet distinguishable particles.
- Let the total number of particles in the system be ‘n’.
- The total volume of the system is fixed and is given by ‘V’.
- The total amount of the energy is fixed and is given by ‘U’.
We now want to know the number of particles at a given energy level.
The energy levels available within the system are given by ε0, ε1, ε2 ………., εr. The energy levels are fixed for the system.
The number of particles sitting at each energy level is variable, and the number of particles is given by n1, n2, n3 …….., nr.
The number of ways to attain a given microstate is given by the formula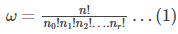
We need to know the combination of n1,n2,n3 up to nr that maximizes the value of ω. This combination results in the most probable microstate. If it is the most probable state, then it can be considered the equilibrium state. To find the combination, let us alter eq (1) as follows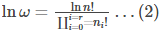
To maximise the value of ω, instead of dealing with ω let us deal with \lnω.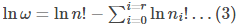
According to Sterling’s approximation, the log of factorial can be approximated as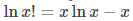
Making use of the Stirling approximation in eq (3), we get
By taking the derivative of the above equation, we get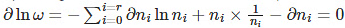
The above equation implies that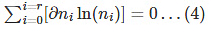
As we know that n is a constant, therefore we can say that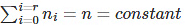
This means that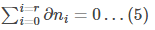
The sum of all the changes in the system should sum up to zero.
The total energy of the system should also be constant.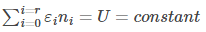
Differentiating the above equation, we get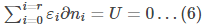
To maximise the function (4) subjected to constraints (5) and (6), let us use Lagrange’s method of undetermined multipliers.
Multiplying (5) by ɑ and multiplying (6) by 𝛽 and then adding 4, 5 and 6, we get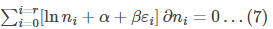
From eq (7) to be zero, the term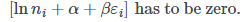
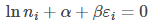
Simplifying the above equation, we get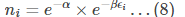
The above equation signifies the number of particles in i th level.
In eq (8), the only variable parameter is ω, therefore taking the sum, we get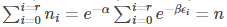
Simplifying, we get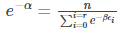
The above equation is the same as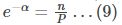
where P is the partition function,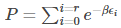
Substituting (9) in (8), we get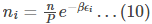
The value of 𝛽 in the above equation is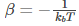
where kb is the Boltzmann constant and T is the temperature.
Substituting the value of 𝛽 in eq (10), we get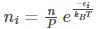
The above expression helps find the number of particles in the most probable microstate. This expression is known as the Maxwell Boltzmann statistics expression.
Kinetic Theory of Gases
The kinetic theory of gases relates the macroscopic property of the gas, like – Temperature, Pressure, and Volume to the microscopic property of the gas, like – speed, momentum, and position. In this model, the atoms and molecules are continually in random motion, constantly colliding with one another and the walls of the container within which the gas is enclosed. It is this motion that results in physical properties such as heat and pressure. In this article, let us delve deeper into the kinetic theory of gases.
What is the Kinetic Theory of Gases?
The gases are made up of a large number of molecules and they are flying in a random direction at a certain speed. By knowing their speed or position, one can figure out the macroscopic properties. In other words, by knowing the value of velocity or the internal energy of gas molecules, one should be able to figure out the temperature or pressure.
Assumptions of Kinetic theory
The Kinetic theory of gases makes some basic assumptions. They are as follows:Kinetic Theory Assumptions
- The molecules do not interact with each other.
- The collision of molecules with themselves or walls will be an elastic collision.
- The momentum is conserved.
- Kinetic energy will be conserved.
How Is the Kinetic Theory of Gases Derived?
Consider a cubic box of length l filled with the gas molecule of mass m, moving along the x-axis with velocity vx Therefore its momentum is mvx.
The gas molecules collide with the walls. At wall 1, it collides and gains momentum mvx.
Similarly, the molecules collide wall 2, reversing the momentum i.e., -mvx.
Thus, the change in the momentum is given by
Δp = mvx-(-mvx) = 2mvx—–(1)
After the collision, the molecule travels a distance of 2l before colliding again with wall 1.
Thus, the time taken is given by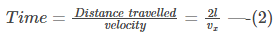
These continuous collisions carry a force, given by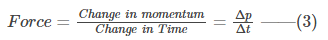
Thus, by substituting the values from equations (1) and (2), we get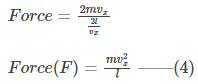
The continuous collisions also exert pressure on the wall given by-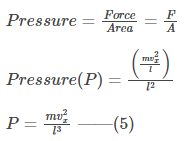
We know that the gas is made of N numbers of molecules and moves in all possible directions. Thus, the pressure exerted on wall 1 by the collision of N number of gas molecules is given by-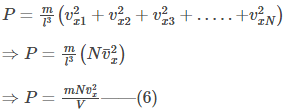
where,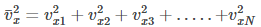
is the average velocity (or velocity component) of all gas molecules colliding with wall 1 along x
direction.
And l3 = V
On extending the above equation to three dimensions, we get-
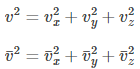
For a large number of gas molecules:
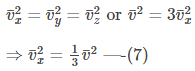
Substituting equation (7) in equation (6), we get
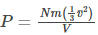
On rearranging,
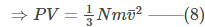
What Is the Average Kinetic Energy of a Gas Molecule?
We know that PV=nRT —(9)
Thus equating equations (8) and (9), we get-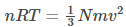
Multiplying and Dividing by 2, we get-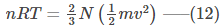
Rearranging equation (10), we get-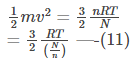
Here, N is the total number of gas molecules in a given region of space
n is the number of moles of gas present in a given region of space.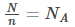
Avagadro’s number in this context is the number of molecules present in the one mole of gas.
NA = 6.022140857 × 1023.
Substituting NA in equation (11),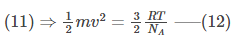
Thus, Average Kinetic Energy of a gas molecule is given by-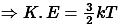
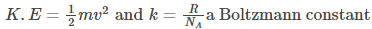
For monoatomic molecules, the total internal energy is given by-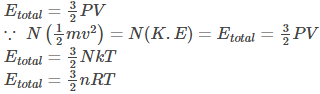
What Is the Significance of the Kinetic Theory of Gases?
- By knowing the Temperature we can directly figure out the average Kinetic energy of a gas molecule. No matter what gas you are considering. Unless and until it is an ideal gas.
- Knowing the macroscopic parameters of gases like Pressure, Volume, Temperature etc., one can accurately calculate the microscopic parameters like Momentum, Velocity, Internal energy, Kinetic energy, Thermal energy etc. and Vise-Versa.
Van der Waals Equation Derivation
According to the ideal gas law, PV = nRT, where P is the pressure, V is the volume, n is the number of moles, T is the temperature, and R is the universal gas constant. The Van der Waals equation is also known as the Van der Waals equation of state for real gases which do not follow ideal gas law. The Van der Waals Equation derivation is explained below.
Derivation of Van der Waals equation
For a real gas, using the Van der Waals equation, the volume of a real gas is given as (Vm – b), where b is the volume occupied per mole.Therefore, ideal gas law when substituted with V = Vm – b is given as:
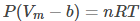
Because of intermolecular attraction, P was modified as below.
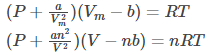
Where,
Vm: molar volume of the gas
R: universal gas constant
T: temperature
P: pressure
V: volume
Thus, Van der Waals equation can be reduced to ideal gas law as PVm = RT.
Van der Waals Equation Derivation for one mole of gas
Following is the derivation of Van der Waals equation for one mole of gas that is composed of non-interacting point particles which satisfies ideal gas law: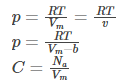
(proportionality between particle surface and number density)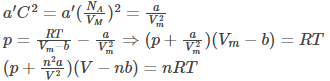
(substituting nVm = V)
Van der Waals equation applied to compressible fluids
Compressible fluids like polymers have varying specific volume which can be written as follows:
Where,
(p + A)(V - B) = CT
p: pressure
V: specific volume
T: temperature
A,B,C: parameters
This was the derivation of Van der Waals equation. Stay tuned with BYJU’S and learn various other Physics related topics.
|
142 videos|312 docs|132 tests
|




















