Introduction: Percents | Mathematics for ACT PDF Download

When we say "Percent" we are really saying "per 100"

One percent (1%) means 1 per 100.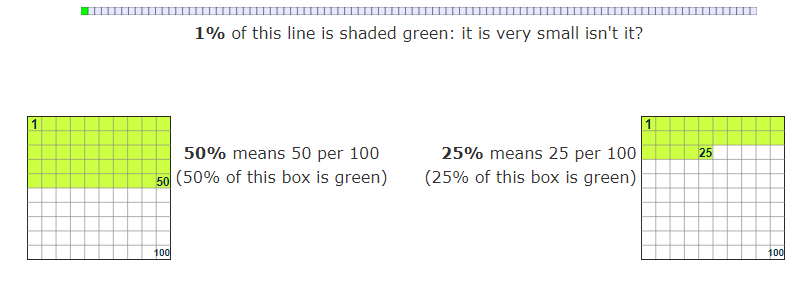

Examples

Example 1: 100% means all
Ans:

Example 2: 50% means half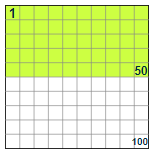
Ans:

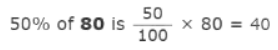
Example 3: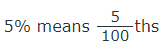

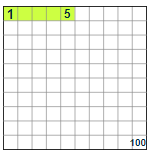Ans: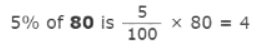

Using Percent

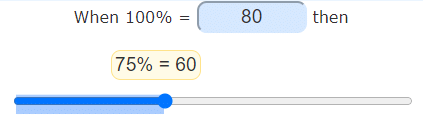Use the slider and try some different numbers
(What is 40% of 80? What is 10% of 200? What is 90% of 10?) 

Because "Percent" means "per 100" think:

"this should be divided by 100"
So 75% really means  75/100
And 100% is  100/100, or exactly 1
(100% of any number is just the number, unchanged)
And 200% is 200/100, or exactly 2
(200% of any number is twice the number)

A Percent can also be expressed as a Decimal or a Fraction

Examples

Example 1: Calculate 25% of 80
Ans: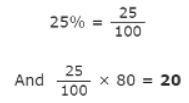

So 25% of 80 is 20

Example 2: 15% of 200 apples are bad. How many apples are bad?
Ans: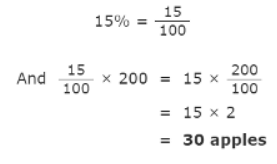

30 apples are bad

Example 3: If only 10 of the 200 apples are bad, what percent is that?
Ans: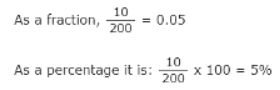

5% of those apples are bad

Example 4: A Skateboard is reduced 25% in price. The old price was $120. Find the new price.
Ans: First, find 25% of $120: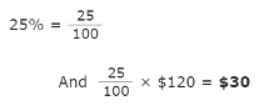

25% of $120 is $30
So the reduction is $30
Take the reduction from the original price
$120 − $30 = $90
The Price of the Skateboard in the sale is $90

Calculation Trick

This little rule can make some calculations easier:
x% of y = y% of x

Example: 8% of 50
Ans: 8% of 50 is the same as 50% of 8
And 50% of 8 is 4
So 8% of 50 is also 4

The Word

"Percent" comes from the latin Per Centum. The latin word Centum means 100, for example a Century is 100 years.

Percent Changes as Multipliers

This is one of the BIG math ideas for GMAT.  A multiplier is a factor by which you multiply a number to get a desired result. There are three percent-related multipliers you will need to understand
a) X% of a number
Suppose I have $400 in an account, and need to know what 30% of this account is.  The multiplier = the percent as a decimal.  30% as a decimal is 0.30, and $400(0.30) = $120, so $120 is 30% of $400.
b) an X% increase
Suppose I have $400 in an account, over time period, I am going to get an additional 5% of interest; in other word, my account is going to increase by 5%.  Here, the multiplier = 1 + (the percent as a decimal).  Thus, $400(1.05) = $420, so that’s the amount I would have after a 5% increase
c) an X% decrease
Suppose I have $400 in an account, and because of some kind of penalty, I am going to be nailed with a 15% deduction; in other words, my account will decrease by 15%.  Here, the multiplier = 1 – (the percent as a decimal).  In this case, the multiplier = 1 – 0.15 = 0.85, and the result after the deduction is ($400)(0.85) = $340.

Calculating a percent change

Basically, a percent is a simple part/whole ratio times 100.  The GMAT will ask you to calculate percent changes, and here you have to be very careful with order, i.e., what’s the starting number and what’s the ending number.  IMPORTANT: in a percent change, the starting number is always 100%.  Thus, we can say: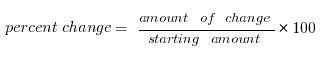
Here are a couple of examples:
(a) Price increases from $400 to $500; find the percentage increase.
Of course, that’s a change of $100, so $100 divided by starting value of $400 is 0.25, times 100 is 25%.  A move from $400 to $500 is a 25% increase.
(b) Price decreases from $500 to $400; find the percentage decrease.
Change is still $100, but now the starting value is $500, and $100/$500 = 0.20, times 100 is 20%.  A move from $500 to $400 is a 20% decrease.

BIG IDEA: Order matters.  When you change from one value to another and want the percentage change, it matters which value was the starting value.

A Series of Percentage Changes

Example: “Profits increased by 40% in January, then decreased by 30% in February, then increased by 20% in March.  Express the change over the entire first quarter as a single percentage.”  This may seem like a nightmare problem, but it’s quite approachable with multipliers.  First Caution: NEVER add a series of percent.  That’s what many people will do, and on multiple choice, it’s always an answer choice – here, that would be 40 – 30 + 20 = 30.  That is not the way to go about answering the question.
The way to attack this question is with a series of multipliers:

• In January, a 40% increase –> multiplier = 1.40
• In February, a 30% decrease –> multiplier = 0.70
• In March, a 20% increase –> multiplier = 1.20
• Aggregate change = (1.40)(0.70)(1.20) = 1.176 –> that’s a 17.6% increase for the quarter.

BIG IDEA: For a series of percentage changes, simply multiply the respective multipliers.

The Increase – Decrease Trap

This is a predictable GMAT Math trap: the result of a percentage increase, followed by a percentage decrease of the same numerical value.  For example, “The price of the appliance increase 20%, and then decreased 20%.  The final price is what percent of the original price.”  Every single time that question is asked on multiple choice, the incorrect answer of 100% will be an answer choice, and every single time, a large portion of folks who take the GMAT will select it.  You have a leg up if you simply recognize and remember that this is a trap.

In fact, solving this problem is just an extension of the previous item:
a 20% increase –> multiplier = 1.20
a 20% decrease –> multiplier = 0.80
total change = (1.20)(0.80) = 0.96
Thus, after the increase and decrease, the final price is 96% of the original price, which means it is a 4% decrease.
BIG IDEA #1: when you go up by a percent, then down by the same percent, you do not wind up where you started: that’s the trap.
BIG IDEA #2: in this situation, as in any situation in which you have a series of percentage changes, simply multiply the respective multipliers.
If you simply remain clear on these five tips, you will be a master of percent & percentage change, one of the most frequently asked topics on GMAT Math.

Special Note: To find out where percents sit in the “big picture” of GMAT Quant, and what other Quant concepts you should study, check out our post entitled:

Solved Examples

Example 1: Geri earns a commission of 22.5% on everything she sells for KM Cosmetics. As of the fifteenth of the month, she has sold $2,100 worth of cosmetics. How much more in cosmetics must she sell in order to earn at least $900 commission for the month?
(a) She has already sold enough to earn $900 commission.
(b) $2,100
(c) $1,300
(d) $4,000
(e) $1,900
Ans: (e)
Explanation: Commission can be calculated by muliplying the commission rate - 22.5%, or 0.225 - by the amount of sales, so the amount of sales needed can be found by dividing the desired commission by 0.225.
$900 ÷ 0.225 = $4,000
Since Geri has already sold $2,100 worth of cosmetics, she needs to sell $4,000 − 2,100 = $1,900 more.

Example 2: 37% of the greatest common factor of 50 and 350 is
(a) 9.25
(b) 129.5
(c) 1.85
(d) 37
(e) 18.5
Ans: (e)
Explanation: The greatest common factor of 50 and 350 is simply 50.  Now we must take 37% of 50.
.37⋅50 = 18.5.

Example 3: Max the cat has 70 toy mice. If 30% of the mice are new, how many mice are not new?
(a) 60
(b) 49
(c) 30
(d) 40
(e) 21
Ans: (b)
Explanation: If 30% of the mice are new, then 70% are not new.
0.7 x 70 = 49.