Triangles Chapter Notes | Mathematics for Class 5 PDF Download
| Table of contents |

|
| Definition |

|
| Properties |

|
| Perimeter of Triangle |

|
| Area of a Triangle |

|
| Area of Triangle Using Heron’s Formula |

|
"Have you ever wondered why bridges and buildings use triangles in their design? Triangles are known as the strongest shapes.

Let’s explore how this simple three-sided shape holds the key to stability and strength all around us!"
Definition

- A triangle is a specific polygon with three sides.
- It has threeedges (sides) and three vertices (corners).
- The angle between these two sides is a crucial concept in geometry.
Triangle Angles
- A triangle comprises three angles, created by meeting two sides at a common point called the vertex.
- The total of the three interior angles equals 180 degrees.
- When extending a side outward, it forms an exterior angle.
- A triangle's combined sum of consecutive interior and exterior angles is supplementary.
- Let's designate the interior angles of a triangle as ∠1, ∠2, and ∠3.
- Extending the sides outward results in three consecutive exterior angles, ∠4, ∠5, and ∠6, corresponding to ∠1, ∠2, and ∠3, respectively.
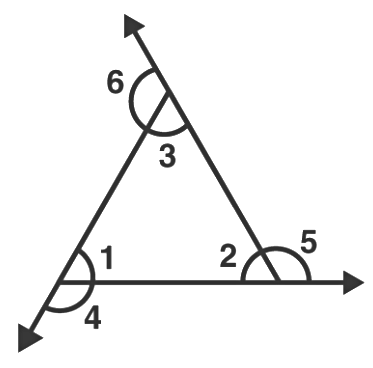
Hence,
- ∠1 + ∠4 = 180° ……(i)
∠2 + ∠5 = 180° …..(ii)
∠3 + ∠6 = 180° …..(iii) - If we add the above three equations, we get;
∠1+∠2+∠3+∠4+∠5+∠6 = 180° + 180° + 180° - Now, by angle sum property we know,
∠1+∠2+∠3 = 180° - Therefore,
180 + ∠4+∠5+∠6 = 180° + 180° + 180°
∠4+∠5+∠6 = 360° - This proves that the sum of the exterior angles of a triangle is equal to 360 degrees.
Properties
Every shape in Maths has some properties which distinguish them from each other. Let us discuss here some of the properties of triangles.
- A triangle has three sides and three angles.
- The sum of the angles of a triangle is always 180 degrees.
- The exterior angles of a triangle always add up to 360 degrees.
- The sum of consecutive interior and exterior angles is supplementary(180 degrees).
- The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Similarly, the difference between the lengths of any two sides of a triangle is less than the length of the third side.
- The shortest side is always opposite the smallest interior angle.
- Similarly, the longest side is always opposite the largest interior angle.
Types of Triangle
The classification of triangles is based on two criteria
1. On the basis of length of the sides.
2. On the basis of measurement of the angles.
1. On the basis of length of the sides, triangles are classified into three categories
- Scalene Triangle
- Isosceles Triangle
- Equilateral Triangle
1. Scalene Triangle
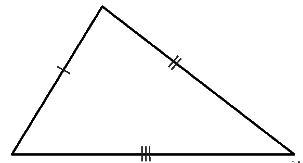
A scalene triangle is a type of triangle, in which all the three sides have different side measures. Due to this, the three angles are also different from each other.
2. Isosceles Triangle
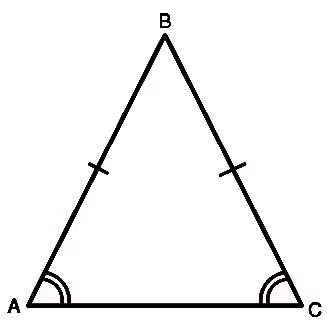 In an isosceles triangle, two sides have equal length. The two angles opposite to the two equal sides are also equal to each other.
In an isosceles triangle, two sides have equal length. The two angles opposite to the two equal sides are also equal to each other.
3. Equilateral Triangle
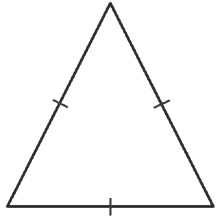
An equilateral triangle has all three sides equal to each other. Due to this all the internal angles are of equal degrees, i.e. each of the angles is 60°
2. On the basis of measurement of the angles, triangles are classified into three categories
- Acute Angle Triangle
- Right Angle Triangle
- Obtuse Angle Triangle
1. Acute Angled Triangle
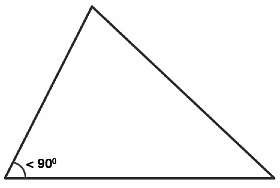
- An acute triangle has all of its angles less than 90°.
2. Right Angled Triangle
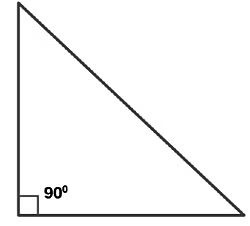
- In a right triangle, one of the angles is equal to 90° or right angle.
3. Obtuse Angled Triangle
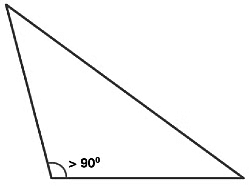
- An obtuse triangle has any of its one angles more than 90°.
Perimeter of Triangle
- The perimeter of a triangle is the complete length around its outer boundary. Another way to express this is that the perimeter is the sum of all three sides of the triangle. The unit of measurement for the perimeter is the same as the unit used for the triangle's sides.
- Perimeter = Sum of All Sides
- If ABC is a triangle, where AB, BC and AC are the lengths of its sides, then the perimeter of ABC is given by:
Perimeter = AB+BC+AC
Area of a Triangle
- The area of a triangle is the space it takes up in a flat, two-dimensional area. Triangles can have different areas based on their sizes.
- We can figure out the area by using the base length and height of the triangle.
- The measurement for the area is given in square units.
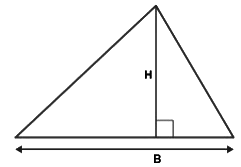
- Suppose a triangle with base ‘B’ and height ‘H’ is given to us, then, the area of a triangle is given by
Area of triangle = Half of Product of Base and Height
Area = 1/2 × Base × Height
Example: Find the area of a triangle having base equal to 9 cm and height equal to 6 cm.
Sol: We know that Area = 1/2 × Base × Height
= 1/2 × 9 × 6 cm2
= 27 cm2
Area of Triangle Using Heron’s Formula
- In case, if the height of a triangle is not given, we cannot be able to use the above formula to find the area of a triangle.
- Therefore, Heron’s formula is used to calculate the area of a triangle, if all the sides lengths are known.
- First, we need to calculate the semi-perimeter (s).
s = (a+b+c)/2, (where a,b,c are the three sides of a triangle) - Now Area is given by; A = √[s(s-a)(s-b)(s-c)]
Example 1: If ABC is a triangle where AB = 3cm, BC=5cm and AC = 4cm, then find its perimeter.
Sol: Given, ABC is a triangle.
AB = 3cm
BC = 5cm
AC = 4cm
As we know by the formula,
Perimeter = Sum of all three sides
P = AB + BC + AC
P = 3+5+4
P = 12cm
Example 2: Find the area of a triangle having sides 5,6 and 7 units length.
Sol: Using Heron’s formula to find the area of a triangle-
Semiperimeter (s) = (a+b+c)/2
s = (5 + 6 +7)/2
s = 9
Now Area of a triangle = √[s(s-a)(s-b)(s-c)]
=√[9(9-5)(9-6)(9-7)]
=√ [9 × 4 × 3 × 2]
=√ [3 × 3 × 2 × 2 × 3 × 2]
=√ [32 × 22 × 3 × 2]
= 6√6 square units.
|
56 videos|187 docs|40 tests
|
FAQs on Triangles Chapter Notes - Mathematics for Class 5
| 1. What is a triangle and how is it defined? |  |
| 2. What are the different types of triangles based on their sides? |  |
| 3. How do you calculate the perimeter of a triangle? |  |
| 4. What is the formula to find the area of a triangle? |  |
| 5. How does Heron’s formula work for finding the area of a triangle? |  |




















