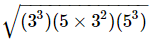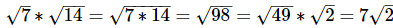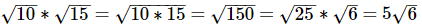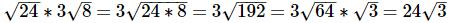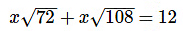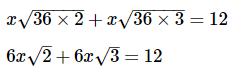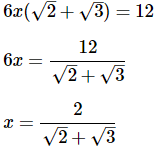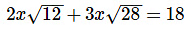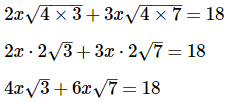Solved Examples: Square Roots | Mathematics for Digital SAT PDF Download
Q1: Simplify: (3x − 4)2
(a) 9x2 − 24x + 16
(b) 9x2 − 24x − 16
(c) 9x2 − 16
(d) 9x2 + 24x + 16
(e) 9x2 + 16
Ans: (a)
If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:
(3x − 4)2 = (3x − 4)(3x − 4)
= 9x2 − 12x − 12x + 16
= 9x2 − 24x + 16
Q2: Simplify: (3n + 5)2
(a) 9n2 + 8n + 25
(b) 9n2 + 8n + 10
(c) 9n2 − 25
(d) 9n2 + 30n + 25
(e) 9n2 + 25
Ans: (d)
If you don't already have the pattern memorized, use FOIL. It's best to write out the parentheses twice (as below) to avoid mistakes:
(3n + 5)2
(3n + 5)(3n + 5)
9n2 + 15n + 15n + 25
9n2 + 30n + 25
Q3: x2 = 36
Quantity A: x
Quantity B: 6
(a) The relationship cannot be determined from the information given
(b) Quantity A is greater
(c) Quantity B is greater
(d) The two quantities are equal
Ans: (a)
x2 = 36 : it is important to remember that this leads to two answers.
x = 6 or x = -6.
If x = 6: A = B.
If x = -6: A < B.
Thus the relationship cannot be determined from the information given.
Q4: Which of the following expressions is equal to the following expression?
√(27)(45)(125)
(a) 225√3
(b) 125√27
(c) 135√5
(d) 205√3
(e) 75√20
Ans: (a)
First, break down the component parts of the square root:
Combine like terms in a way that will let you pull some of them out from underneath the square root symbol:
Pull out the terms with even exponents and simplify:
(52)(32)√3
= 225√3
Q5: Simplify: (3 + 5i) + (4 − 2i) + (−2 + i)
(a) 5+4i
(b) 9−8i
(c) 9+8i
(d) 5−4i
(e) 10−9i
Ans: (a)
It can be easier to line real and imaginary parts vertically to keep things organized, but in essence, combine like terms (where 'like' here means real or imaginary):
(3 + 5i) + (4 − 2i) + (−2 + i)
=3 + 4 + (−2) + 5i + (−2i) + i
=5 + 4i
Q6: Simplify: √7 x √14
(a) 9√8
(b) 2√7
(c) 7√3
(d) √21
(e) 7√2
Ans: (e)
When multiplying square roots, you are allowed to multiply the numbers inside the square root. Then simplify if necessary.
Q7: Simplify: √10 x √15
(a) 10√2
(b) 5√6
(c) 6√5
(d) 75√2
(e) √150
Ans: (b)
When multiplying square roots, you are allowed to multiply the numbers inside the square root. Then simplify if necessary.
Q8: Simplify: √ 24 x 3√ 8
(a) 24√ 6
(b) 12√ 3
(c) 24√ 3
(d) 81√ 4
(e) 16√ 6
Ans: (c)
When multiplying square roots, you are allowed to multiply the numbers inside the square root. Then simplify if necessary.
Q9: Solve for x:
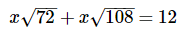
(a) 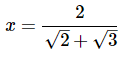
(b) 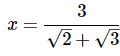
(c) 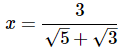
(d) 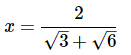
(e) 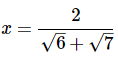
Ans: (a)
Note that all of the square root terms share a common factor of 36, which itself is a square of 6:
Factoring 6x from both terms on the left side of the equation:
Q10: Solve for x: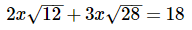
(a) 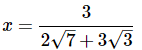
(b) 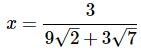
(c) 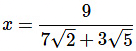
(d) 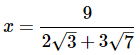
(e) 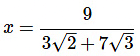
Ans: (d)
Note that both √12 and √28 have a common factor of 4 and 4 is a perfect square:
From here, we can factor 2x out of both terms on the left hand side
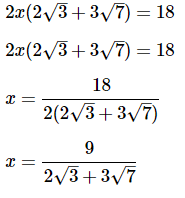
|
204 videos|126 docs|75 tests
|