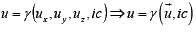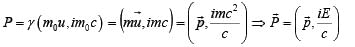Special Theory of Relativity | Modern Physics PDF Download
| Table of contents |

|
| Relative Velocity |

|
| Relativistic Mass |

|
| Relativistic Second Law of Motion |

|
| Relativistic Energy |

|
| The Doppler Effect in Light |

|
| Four Vectors and Relativistic Invariance |

|
Relative Velocity
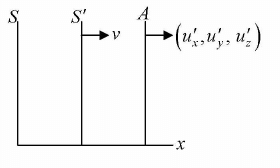
There is one inertial frame S, S’ is another inertial frame moving with respect to S in the x-direction and A is another inertial frame which is moving with respect to S' with velocity component (u'x, u'y, u'z)
So, u'x = dx'/dt' u'y = dy'/dt' u'z = dz'/dt'
The velocity component of A from the S frame is given by
ux = dx/dt , uy = dy/dt , uz = dz/dt
From the inverse Lorentz Transformation,

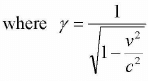
Differentiating both sides, we get
dx = γ(dx’ + vdt') , dy = dy', dz = dz',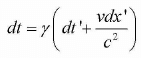
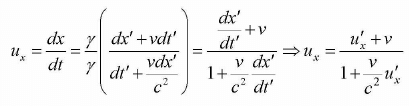
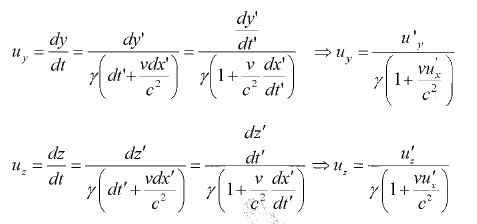
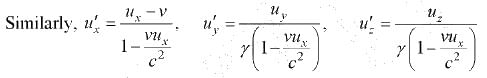
Relativistic Mass
The mass of a body moving at a speed v relative to an observer is larger than its mass when it is at rest relative to the observer by the factor
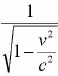
Thus,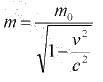
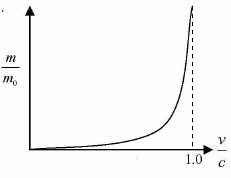
where m0 is the rest mass of the body and m is the observed mass.
Relativistic Momentum
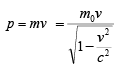
Relativistic Second Law of Motion
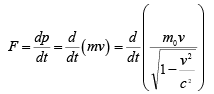
Relativistic Energy
Einstein suggested, that if m is the relativistic mass of the body then relativistic energy E is given by

Rest Energy
If the rest mass of a particle is m0 then the rest mass energy is given by moc2
Relativistic Kinetic Energy
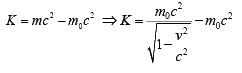
Relationship between total Energy and Momentum
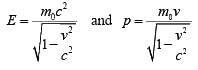
E2 = /W20C4 + p2c2 ⇒ E = (/W20C4 + p2c2)1/2
The Doppler Effect in Light
The Doppler Effect in sound varies depending on whether the source, the observer, or both are moving, which appears to violate the principle of relativity. All that should count is the relative motion of the source and observer. But sound waves occur only in a material medium such as air or water, and this medium is itself a frame of reference with respect to which motions of the source and observer are measurable. Hence, there is no contradiction. In the case of light, however, no medium is involved and only the relative motion of the source and observer is meaningful. The Doppler Effect in light therefore must differ from that in sound.
We can analyze the Doppler Effect in light by considering a light source as a clock that ticks v0 times per second and emits a wave of light with each tick. We will examine the three situations as shown in the figure given below.
Transverse Doppler Effect in Light
The observer is moving perpendicular to a line between him and the light source. The proper time between ticks is t0 = 1/v0, so between one tick and the next tick, time
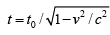
elapses in the reference frame of the observer.

The frequency he finds is accordingly,
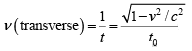
The observed frequency v is always less than the source frequency v0.
Observer and Source Moving Apart
The observer is receding from the light source. Now the observer travels the distance vt away from the source between ticks, which mean that the light wave from a given tick takes vt/c longer to reach him than the previous one. Hence, the total time between the arrivals of successive waves is
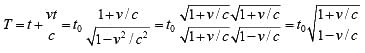
and the observed frequency is
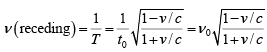
The observed frequency v is lower than the source frequency v0. Unlike the case of sound waves, which propagate relative to a material medium, it makes no difference whether the observer is moving away from the source or the source is moving away from the observer.
Observer and Source Moving Towards Each Other (Approaching)
The observer is approaching the light source. The observer here travels the distance vt toward the source between ticks, so each light wave takes vt / c less time to arrive than the previous one. In this case, T = t - vt / c and the result is
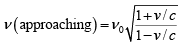

The observed frequency is higher than the source frequency. Again, the same formula holds for the motion of the source toward the observer.
Four Vectors and Relativistic Invariance
- Four position vector, ds = (dx, dy, dz, icdt)
- Four velocity vector,


- Four momentum – Four Energy vectors,

- Four Force,

Four Dimensional Space-Time Continuums
The square of the interval is represented as
S212 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2 - c2(t2 - t1)2
S212 = r212 - c2(t2 - t1)2
(i) Space-like Intervals: The time separation between the two events is less than the time taken by light to cover the distance between them.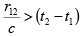
(ii) Time-like intervals: The time separation between two events is more than the time taken by light to cover the distance between them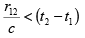
(iii) Light-like intervals: The Time separation between two events is equal to the time taken by light to cover the distance between them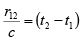
Example 1: Determine the length and the orientation of a rod of length l0 in a frame of reference which is moving with v velocity in a direction making θ angle with rod.
Proper length of the rod in the direction of moving frame Ix = l0 cos θ, the length measured in the moving frame
Example 2: A cube of density ρo in the rest frame is moving with velocity v with respect to the observer parallel to one of its edges. What is density measured by the observer?
In rest frame m0/V0 = ρo and from moving frame ρ = mass/volume
and relativistic volume
Example 3: A spaceship is moving away from the Earth with a velocity of 0.5c and fires a rocket whose velocity relative to space is 0.5c (a) Away from Earth (b) Towards the Earth. Calculate the velocity of the rocket as observed from the earth in two cases.
(a) u' = 0.5c, v = 0.5c
(b) u' = -0.5c, v = 0.5c
Example 4: Show that the rest mass of the particle of momentum p and kinetic energy T given by 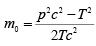
E = EK + E0 ⇒ E = T + m0c2
E2 = p2c2 + m20c4
Example 5: A π-meson at rest mass mx decays into p-meson of mass mμ and neutrino of mass mv. Find the total energy of μ -meson.
Ex = mxc2, E2μ = p2μc2 + m2μc4, E2v = p2vc2 + m2vc4
From conservation of energy Ex = Eμ + Ev and from conservation of momentum
Pv = -Pμ = P
Using, E2μ - E2v = (m2μ - m2v)c4 and Ex = Eμ + Ev
Example 6: The rate of a clock in spaceship Suryashakti is observed from Earth to be 3/5 at the rate of the clock on Earth.
(a) What is the speed of spaceship Suryashakti relative to Earth?
(b) If the rate of the clock in spaceship Akashganga is observed from Earth to be 5/13 at the rate of the clocks on Earth. If both Aakashganga and Suryashakti are moving in the same direction relative to someone on Earth, then what is the speed of Aakashganga relative to Suryashakti?
(a) From the time dilation
The velocity of Suryashakti is (4/5)c
(b) Similarly,
Velocity of Akashganga with respect to Suryashakti is given
Hence, both are moving in same direction
Velocity of Aakashganga with respect to Suryashakti is
Example 7: In the laboratory frame, a particle P at rest mass m0 is moving in the positive x-direction with the speed of 5c/19. It approaches an identical particle Q moving in the negative x-direction with a speed of 2c/5.
(a) What is the speed of the particle P in the rest frame of the particle Q?
(b) What is the Energy of the particle P in the rest frame of the particle Q?
Example 8: The mass m of a moving particle is 2m0/√3, where m0 is its rest mass. Then what is the linear momentum of the particle?
Example 9: A distant galaxy in the constellation Hydra is receding from the earth at 6.12 x 107 m /s by how much is a green spectral line of wavelength 500 nm emitted by this galaxy shifted towards the red at spectrum.
since v = 0.204c, λ0 = 500
which is orange part of spectrum. The shift is λ - λ0 = 115 nm
|
37 videos|16 docs|19 tests
|

|
Explore Courses for Physics exam
|

|