Understanding Pauli's Exclusion Principle | Chemistry for EmSAT Achieve PDF Download
The Pauli Exclusion Principle holds significant importance in Chemistry, alongside the Aufbau Principle and Hund’s Rule. It is essential for students, particularly when delving into the study of electrons. This principle aids in comprehending the arrangement of electrons within atoms and molecules, providing insight into the classification of elements within the periodic table. This section will delve into a detailed examination of the Pauli Exclusion Principle, covering all associated concepts comprehensively.
What is the Pauli Exclusion Principle?
The Pauli Exclusion Principle dictates that within a single atom, no two electrons can possess identical sets of quantum numbers (n, l, ml, and ms). Simply put, each electron must occupy its own unique state, known as a singlet state. This principle adheres to two key rules:
- Only a maximum of two electrons can occupy a single orbital.
- Electrons sharing the same orbital must have opposite spins, or their spins must be antiparallel.
However, it's important to note that the Pauli Exclusion Principle isn't exclusive to electrons; it also applies to other particles with half-integer spin, such as fermions. Conversely, it doesn't apply to particles with integer spin, like bosons, which exhibit symmetric wave functions. Unlike fermions, bosons can share quantum states without restriction. Fermions derive their name from the Fermi–Dirac statistical distribution they obey, while bosons are named after the Bose-Einstein distribution function they follow.
Formulation of the Principle
The principle was formulated by the Austrian physicist Wolfgang Pauli in 1925, elucidating the behavior of electrons. In 1940, he further developed the principle to encompass all fermions through his spin-statistics theorem. Notably, fermions described by this principle include elementary particles like quarks, electrons, neutrinos, and baryons. For his discovery of the Pauli exclusion principle and his broader contributions to quantum mechanics, Wolfgang Pauli was awarded the Nobel Prize in 1945. Albert Einstein nominated him for this prestigious accolade.
Pauli Exclusion Principle in Chemistry
In chemistry, the Pauli Exclusion Principle is primarily employed to elucidate and establish the electron shell configuration of atoms, as well as to anticipate which atoms are inclined to donate electrons. How does this principle function and where does it find application? When observing atoms, upon acquiring new electrons, they typically transition to the lowest energy state or migrate to the outermost shell. If a state contains a solitary electron, it may exhibit either spin up or spin down orientation. However, adhering to the Pauli Exclusion Principle, if there are two electrons within a state, each electron must possess a distinct spin, whether it be spin up or spin down.
Pauli Exclusion Principle Example
A typical illustration of the Pauli Exclusion Principle can be demonstrated through a neutral helium atom. This atom contains two bound electrons, both occupying the outermost shell with opposite spins. Specifically, these two electrons are situated within the 1s subshell, where the quantum numbers are defined as n = 1, l = 0, and ml = 0.
The spin moments of these electrons differ; one having ms = -1/2, while the other possesses +1/2. Representing this scenario diagrammatically, the subshell of the helium atom would depict one "up" electron and one "down" electron. Essentially, the 1s subshell comprises two electrons with opposing spins.
Similarly, considering hydrogen, it features a 1s subshell with a single "up" electron (1s1). Meanwhile, lithium encompasses the helium core (1s2) and an additional "up" electron (2s1). This presentation aims to illustrate the electron configuration of orbitals in the given manner.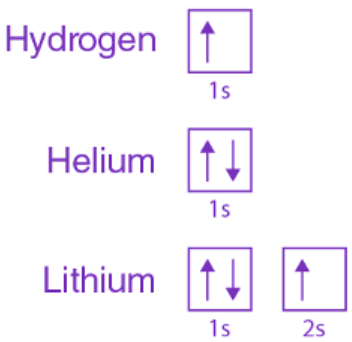
From the above example, we can further deduce that successive larger elements will have shells of successively higher energy. The number of electrons in the outermost shell is also directly related to the different chemical properties that elements possess. Elements with the same number of electrons in the outermost shell will have similar properties.
Nuclear Stability and Pauli Exclusion Principle
- The nuclei within an atom are composed of neutrons and protons, held together by the nuclear force. However, the positively charged protons tend to repel each other via the electromagnetic force. Essentially, these two forces compete against each other, contributing to the stability of the nuclei. Nonetheless, only specific combinations of protons and neutrons result in stable nuclei.
- Neutrons play a significant role in stabilizing the nucleus by attracting each other and the protons, thus mitigating the electrical repulsion between protons. Consequently, an increasing ratio of neutrons to protons is necessary to establish a stable nucleus.
- If there is an excess or deficiency of neutrons relative to the number of protons (bearing in mind that neutrons also adhere to the Pauli Exclusion Principle), the nucleus becomes unstable, leading to radioactive decay. Moreover, the Pauli Exclusion Principle influences the critical energy of fissile and fissionable nuclei.
- For instance, actinides with an odd neutron number are typically fissile, meaning they can undergo fission with slow neutrons. Conversely, actinides with an even neutron number are usually not fissile or fissionable with fast neutrons. Similarly, heavy nuclei with an even number of protons and neutrons exhibit stability due to "paired spin" resulting from the Pauli Exclusion Principle. Conversely, nuclei with an odd number of protons or neutrons are typically unstable.
Importance and Applications of Pauli Exclusion Principle
- The Pauli exclusion principle elucidates phenomena like the electron shell structure of atoms and the sharing of electrons among atoms.
- It aids in understanding the behavior of various chemical elements and their involvement in the formation of chemical bonds.
- The periodic table's organization can be attributed to the application of this principle.
- Solid-state properties, including electrical, optical, magnetic, mechanical, and chemical characteristics, directly arise from the Pauli exclusion principle.
- It contributes to explaining the stability of large systems containing numerous electrons and nucleons.
- Beyond its role in Chemistry, the Pauli exclusion principle serves as a fundamental concept in quantum mechanics, predominantly studied in Physics.
- The principle finds applications in astrophysics as well.
|
191 videos|265 docs|160 tests
|
FAQs on Understanding Pauli's Exclusion Principle - Chemistry for EmSAT Achieve
| 1. What is the Pauli Exclusion Principle and how does it relate to chemistry? |  |
| 2. How is the Pauli Exclusion Principle related to electron configuration? |  |
| 3. What is the significance of the Pauli Exclusion Principle in understanding atomic nuclei stability? |  |
| 4. What are some practical applications of the Pauli Exclusion Principle? |  |
| 5. How did Wolfgang Pauli formulate the Pauli Exclusion Principle? |  |
















