What is Ideal Gas | Chemistry for EmSAT Achieve PDF Download
| Table of contents |

|
| What is Ideal Gas Equation? |

|
| Equation of Ideal Gas Law |

|
| Ideal Gas Equation Units |

|
| What is Ideal gas? |

|
| Ideal Gas Equation in Other Forms |

|
What is Ideal Gas Equation?
In the realm of thermodynamics, the Ideal Gas Law serves as a well-defined approximation for the behavior exhibited by numerous gases across varied conditions. This equation amalgamates empirical principles such as Charle’s, Boyle’s, Gay-Lussac’s, and Avogadro’s laws. The Ideal Gas Equation, also known as the general gas equation, mathematically expresses the states of hypothetical gases through the integration of empirical and physical constants. It can be succinctly described as follows: "The Ideal Gas Law represents the equation of state for a theoretical ideal gas, offering a reasonably accurate portrayal of gas behavior across diverse conditions, albeit with certain limitations."
Equation of Ideal Gas Law
The state of an ideal gas is determined by the macroscopic and microscopic parameters like pressure, volume, temperature. Thus, the ideal gas equation is often written as:
PV = nRT
Where,
- P is the pressure of the ideal gas.
- V is the volume of the ideal gas.
- n is the amount of ideal gas measured in terms of moles.
- R is the gas constant.
- T is the temperature.
The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.
Ideal Gas Equation Units
The Ideal gas equation units, terms, and corresponding definitions can be expressed as follows: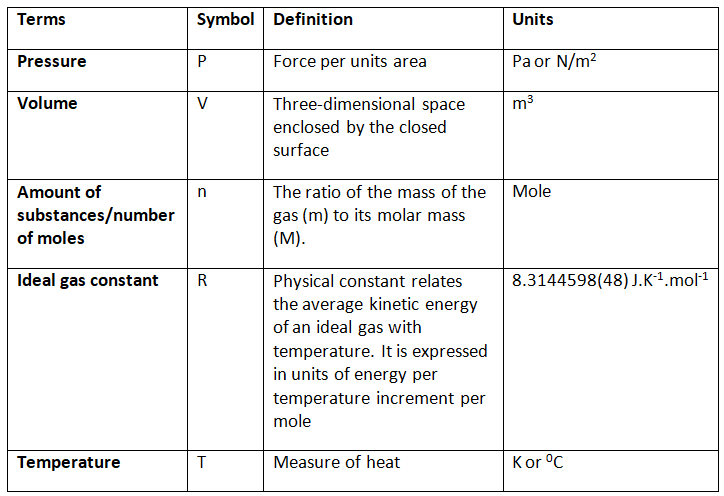
What is Ideal gas?
The concept of an ideal gas is a theoretical construct rather than a physical reality, introduced to simplify calculations.
An ideal gas is an abstract notion comprising of randomly-moving point particles that exclusively interact via elastic collisions.
Within the framework of ideal gas theory, gas molecules move unrestrainedly in all directions, with collisions between them assumed to be perfectly elastic, resulting in no loss of kinetic energy.
While an ideal gas doesn't exist in nature, real gases tend to approximate its properties as their density decreases. This is achievable because at sufficiently low densities, gas molecules are so widely spaced that interactions between them are negligible. Thus, the ideal gas model serves as a useful tool for the study of real gases.
Ideal Gas Equation – Explained
To study the property of gases we need to have a standard gas to study, but which gas should it be? Hydrogen, oxygen, helium, nitrogen, carbon dioxide to name a few, and there are thousands of other gasses we could study.
The researchers have found that no matter what gas you study if you take a one-mole sample of that gas and put it in the same container and maintain a constant temperature, the pressure is almost the same, and at lower densities, even those tiny differences in the measurements also disappear.
Thus, at really low densities, all the real gases tend to obey one universal law called ideal gas law.
This law is described by an equation known as the Ideal gas equation:
PV = nRT
Limitations
Although the ideal gas equation has many limitations.
- This equation holds well as long as the density is kept low.
- This equation is applicable for single gas or even a mixture of multiple gasses where ‘n’ will stand for the total moles of gas particles in the given mixture.
The Equation of States of an ideal gas explains the simple relation between the parameters or properties that are very generic and accurate. In general, an equation relating the relation between P, V, T of an ideal gas is called Equation of States. Sometimes the relation involving other parameters of a substance at equilibrium state is also referred to as the Equation of States.
The simplest equation of state for substances in the gas phase is the ideal-gas equation of state as:
PV =RT
Ideal Gas Equation in Other Forms
The ideal gas equation can be rewritten in multiple ways depending upon the disciplines. Some of them are given below:
Common Form: Most frequently used form of the ideal gas equation is-
PV = nRT = NkBT
Where,
- P is the pressure of the ideal gas.
- V is the volume of the ideal gas.
- n is the amount of ideal gas measured in terms of moles.
- R is the gas constant.
- T is the temperature.
- N is the number of gas molecules (N=NAn)
- kB is the Boltzmann constant.
- NA is the Avogadro’s constant.
Molar form: This alternate form of the ideal gas equation is useful because it specifies the amount of gas accurately. Here instead of the mass of the gas molecules its chemical equivalent mass is used. Thus, the molar form is given as:
Pv = RspecificT
- Where,
P is the pressure of the ideal gas - v is the specific volume given by
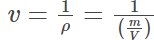
- Rspecific is the specific gas constant given by
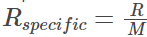
- T is the temperature
Statistical Mechanics
In statistical mechanics, the ideal gas equations are given by:
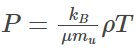
Where,
- P is the pressure of the ideal gas
- T is the temperature.
- μ average particle mass
- mu is the atomic mass constant
- ρ is the density given by ρ = m/V = nμmu
- kB is the Boltzmann constant.
|
191 videos|265 docs|160 tests
|














