Overview: Vectors | Mathematics for ACT PDF Download
| Table of contents |

|
| Introduction |

|
| Vectors in Euclidean Geometry- Definition |

|
| Operations on Vectors |

|
| Scalars and Vectors |

|
| Distinguishing Scalars from Vectors |

|
Introduction
A vector, derived from the Latin word for "carrier," serves to transport a point A to another point B. The distance between these points, known as the magnitude of the vector, defines the length of the line connecting them. Meanwhile, the orientation of the displacement from point A to point B is termed as the direction of the vector AB. Vectors, alternatively known as Euclidean vectors or Spatial vectors, find extensive utility across diverse domains such as mathematics, physics, engineering, and numerous other disciplines.
Vectors in Euclidean Geometry- Definition
Vectors in math is a geometric entity that has both magnitude and direction. Vectors have an initial point at the point where they start and a terminal point that tells the final position of the point. Various operations can be applied to vectors such as addition, subtraction, and multiplication. We will study the operations on vectors in detail in this article.
Vectors - Examples
Vectors play an important role in physics. For example, velocity, displacement, acceleration, force are all vector quantities that have a magnitude as well as a direction.
Representation of Vectors
Vectors are usually represented in bold lowercase such as a or using an arrow over the letter as a . Vectors can also be denoted by their initial and terminal points with an arrow above them, for example, vector AB can be denoted as  The standard form of representation of a vector is
The standard form of representation of a vector is  Here, a,b,c are real numbers and
Here, a,b,c are real numbers and  are the unit vectors along the x-axis, y-axis, and z-axis respectively.
are the unit vectors along the x-axis, y-axis, and z-axis respectively.
The initial point of a vector is also called the tail whereas the terminal point is called the head. Vectors describe the movement of an object from one place to another. In the cartesian coordinate system, vectors can be denoted by ordered pairs. Similarly, vectors in 'n' dimensions can be denoted by an 'n' tuple. Vectors are also identified with a tuple of components which are the scalar coefficients for a set of basis vectors. The basis vectors are denoted as: e1 = (1,0,0), e2 = (0,1,0), e3 = (0,0,1)
Magnitude of Vectors
The magnitude of a vector can be calculated by taking the square root of the sum of the squares of its components. If (x,y,z) are the components of a vector A, then the magnitude formula of A is given by,
- |A| = √ (x2+y2+z2)
The magnitude of a vector is a scalar value.
Angle Between Two Vectors
The angle between two vectors can be calculated using the dot product formula. Let us consider two vectors a and b and the angle between them to be θ. Then, the dot product of two vectors is given by a·b = |a||b| cosθ. We need to determine the value of the angle θ. The angle between two vectors also indicates the directions of the two vectors. θ can be evaluated using the following formula:
θ = cos-1[(a·b)/|a||b|]
Types of Vectors
- The vectors are termed as different types based on their magnitude, direction, and their relationship with other vectors. Let us explore a few types of vectors and their properties:
Zero Vectors
- Vectors that have 0 magnitude are called zero vectors, denoted by
 = (0,0,0). The zero vector has zero magnitudes and no direction. It is also called the additive identity of vectors.
= (0,0,0). The zero vector has zero magnitudes and no direction. It is also called the additive identity of vectors.
Unit Vectors
- Vectors that have magnitude equals to 1 are called unit vectors, denoted by
 It is also called the multiplicative identity of vectors. The magnitude of a unit vectors is 1. It is generally used to denote the direction of a vector.
It is also called the multiplicative identity of vectors. The magnitude of a unit vectors is 1. It is generally used to denote the direction of a vector.
Position Vectors
- Position vectors are used to determine the position and direction of movement of the vectors in a three-dimensional space. The magnitude and direction of position vectors can be changed relative to other bodies. It is also called the location vector.
Equal Vectors
- Two or more vectors are said to be equal if their corresponding components are equal. Equal vectors have the same magnitude as well as direction. They may have different initial and terminal points but the magnitude and direction must be equal.
Negative Vector
- A vector is said to be the negative of another vector if they have the same magnitudes but opposite directions. If vectors A and B have equal magnitude but opposite directions, then vector A is said to be the negative of vector B or vice versa.
Parallel Vectors
- Two or more vectors are said to be parallel vectors if they have the same direction but not necessarily the same magnitude. The angles of the direction of parallel vectors differ by zero degrees. The vectors whose angle of direction differs by 180 degrees are called antiparallel vectors, that is, antiparallel vectors have opposite directions.
Orthogonal Vectors
- Two or more vectors in space are said to be orthogonal if the angle between them is 90 degrees. In other words, the dot product of orthogonal vectors is always 0. a·b = |a|·|b|cos90° = 0.
Co-initial Vectors
- Vectors that have the same initial point are called co-initial vectors.
Vectors Formulas
- Different mathematical operations can be applied to vectors such as addition, subtraction, and multiplication. In this section, we will explore the vector formulas for vector addition, subtraction, dot-product, cross-product and angle between the vectors.
The list of vectors formulas that we will be studying in detail further is as follows:

Properties of Vectors
The following properties of vectors help in better understanding of vectors and are useful in performing numerous arithmetic operations involving vectors.
The addition of vectors is commutative and associative.

The dot product of two vectors is a scalar and lies in the plane of the two vectors. The cross product of two vectors is a vector, which is perpendicular to the plane containing these two vectors.
Operations on Vectors
Some basic operations on vectors can be performed geometrically without taking any coordinate system as a reference. These vector operations are given as addition, subtraction, and multiplication by a scalar. Also, there are two different ways to multiply two vectors together, the dot product and the cross product. These are briefly explained as given below,
- Addition of Vectors
- Subtraction of Vectors
- Scalar Multiplication
- Scalar Triple Product of Vectors
- Multiplication of Vectors
Addition of Vectors
Adding vectors is similar to adding scalars. The individual components of the respective vectors are added to get the final value:

The addition of vectors is commutative and associative. There are two laws of vector addition:
- Triangle Law of Addition of Vectors: The law states that if two sides of a triangle represent the two vectors (both in magnitude and direction) acting simultaneously on a body in the same order, then the third side of the triangle represents the resultant vector.
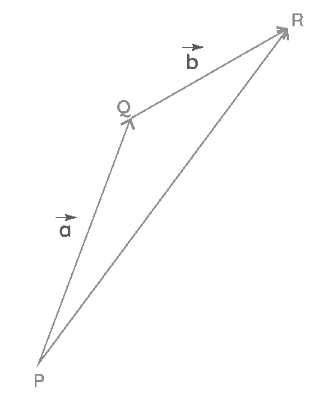
Parallelogram Law of Addition of Vectors: The law states that if two co-initial vectors acting simultaneously are represented by the two adjacent sides of a parallelogram, then the diagonal of the parallelogram represents the sum of the two vectors, that is, the resultant vector starting from the same initial point.

Subtraction of Vectors
The subtraction of vectors is similar to the addition of vectors. But here only the sign of one of the vectors is changed in direction and added to the other vector.

Scalar Multiplication of Vectors
A scalar is a real number that has no direction. When a scalar is multiplied by a vector, we multiply the scalar by each component of the vector. The operation of multiplying a vector by a scalar is called scalar multiplication. a = (a1, a2, a3) = is multiplied by a scalar r, the resultant vector is:
is multiplied by a scalar r, the resultant vector is:
ra = (ra1, ra2, ra3) = (ra1)e1 + (ra2)e2 + (ra3)e3
- If r is negative, then the direction of the resultant vector changes direction by 180 degrees.
- Scalar multiplication is distributive over vector addition, that is, r(a+b) = ra + rb
The multiplication of vectors with any scalar quantity is defined as 'scaling'. Scaling in vectors only alters the magnitude and does not affect the direction. Some properties of scalar multiplication in vectors are given as,
- k(a + b) = ka + kb
- (k + l)a = ka + la
- a·1 = a
- a·0 = 0
- a·(-1) = -a
Scalar Triple Product of Vectors
Scalar triple product of vectors is the dot of one vector with the cross product of the other two vectors. If any two vectors in a scalar triple product are equal, then the scalar triple product is zero. If the scalar triple product is equal to zero, then the three vectors a, b, and c are said to be coplanar.
- Also, a·(b × c) = b·(c × a) = c·(a × b)

Multiplication of Vectors
Vectors can be multiplied but their methods of multiplication are slightly different from that of real numbers. There are two different ways to multiply vectors:
Dot Product of Vectors:
The individual components of the two vectors to be multiplied are multiplied and the result is added to get the dot product of two vectors.

Another way to determine the dot product of two vectors A and B is to determine the product of the magnitudes of the two vectors and the cosine of the angle between them. = |A||B| cosθ
= |A||B| cosθ
The resultant of a dot product of two vectors is a scalar value, that is, it has no direction.
Cross Product of vectors:
The vector components are represented in a matrix and a determinant of the matrix represents the result of the cross product of the vectors.

Another way to determine the cross product of two vectors A and B is to determine the product of the magnitudes of the two vectors and the sine of the angle between them.

Components of Vectors
A vector quantity has two characteristics, magnitude, and direction, such that both the quantities are compared while comparing two vector quantities of the same type. Any vector, in a two-dimensional coordinate system, can be broken into x-component, and y-component. In the figure given below, we can observe these components - x-component, Vx and y-component, Vy for a vector,v in coordinate plane.

The values of Vx and Vy can be given as,
Vx = V·cosθ, and Vy = V.sinθ
|V| = √[Vx2 + Vy2]
Scalars and Vectors
Scalars, in the realm of physical quantities, lack directional attributes and are represented solely by numerical values. These values, often accompanied by unit measurements, encapsulate properties like distance, speed, time, and others. Conversely, vectors embody both magnitudes and directions, delineating quantities such as displacement, velocity, acceleration, force, and more. Basic arithmetic operations, including addition, subtraction, and multiplication, are applicable to both scalars and vectors.
Distinguishing Scalars from Vectors
The fundamental disparity between scalars and vectors lies in their treatment of directionality. Scalars remain indifferent to direction, relying solely on numerical magnitude. In contrast, vectors inherently incorporate directionality alongside magnitude. For instance, while distance and time stand as typical scalar examples, denoted by real values and their respective units, displacement and velocity exemplify vectors, characterizing both magnitude and directionality.
Illustrative Examples:
- Scalar quantities such as speed at 40 mph or time measured at 4 hours exhibit numerical values devoid of directional context.
- Vector quantities like displacement marked as -4 ft or velocity designated as -40 mph signify both magnitude and direction. Negative values signify movement in opposite directions.
Applications of Vectors
Vectors find extensive utility in the realms of Physics and Mathematics, serving as fundamental tools for representing various physical phenomena:
- Vector concepts are integral to the study of partial differential equations and differential geometry, facilitating analyses in complex mathematical frameworks.
- In the fields of physics and engineering, vectors play pivotal roles, especially concerning electromagnetic fields, gravitational fields, and fluid dynamics. They offer indispensable insights into phenomena ranging from electromagnetic interactions to fluid flow patterns.
|
144 videos|100 docs|61 tests
|
FAQs on Overview: Vectors - Mathematics for ACT
| 1. What is the definition of vectors in Euclidean Geometry? |  |
| 2. What are the common operations that can be performed on vectors? |  |
| 3. How are scalars different from vectors? |  |
| 4. How can vectors be distinguished from scalars in a given problem? |  |
| 5. Why are vectors important in Euclidean Geometry and various fields of science and engineering? |  |

|
Explore Courses for ACT exam
|

|
 = (0,0,0). The zero vector has zero magnitudes and no direction. It is also called the additive identity of vectors.
= (0,0,0). The zero vector has zero magnitudes and no direction. It is also called the additive identity of vectors. It is also called the multiplicative identity of vectors. The magnitude of a unit vectors is 1. It is generally used to denote the direction of a vector.
It is also called the multiplicative identity of vectors. The magnitude of a unit vectors is 1. It is generally used to denote the direction of a vector.















