ACT Exam > ACT Notes > Mathematics for ACT > Practice Questions: Matrices
Practice Questions: Matrices | Mathematics for ACT PDF Download
Q1: Evaluate:
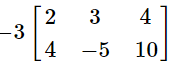
(a)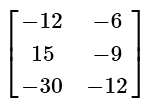
(b)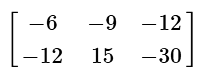
(c)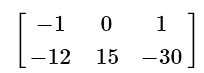
(d)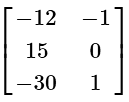
View AnswerAns: (b)
This problem involves a scalar multiplication with a matrix. Simply distribute the negative three and multiply this value with every number in the 2 by 3 matrix. The rows and columns will not change.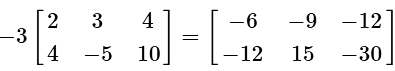
Q2: Simplify: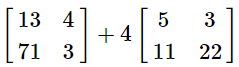
(a)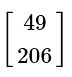
(b)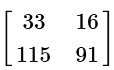
(c)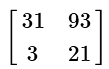
(d)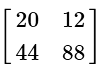
View AnswerAns: (b)
Scalar multiplication and addition of matrices are both very easy. Just like regular scalar values, you do multiplication first: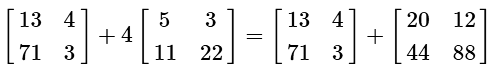
The addition of matrices is very easy. You merely need to add them directly together, correlating the spaces directly.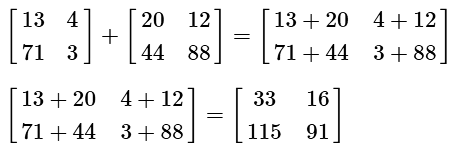
Q3: Simplify the following
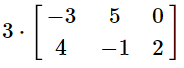
(a)
(b)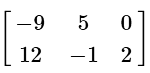
(c)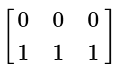
(d)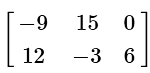
View AnswerAns: (d)
When multplying any matrix by a scalar quantity (3 in our case), we simply multiply each term in the matrix by the scalar.
Therefore, every number simply gets multiplied by 3, giving us our answer.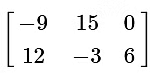
Q4: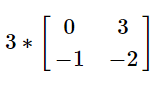
(a)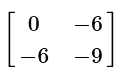
(b)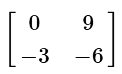
(c)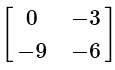
(d)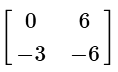
View AnswerAns: (c)
When multiplying a constant to a matrix, multiply each entry in the matrix by the constant.
Q5: With matrix notation, what does M2x3 x N3x4 equal?
(a) None of the answers are correct
(b) P2x4
(c) P3x4
(d) P3x3
View AnswerAns: (b)
M2x3 x N3x4 = P2x4
In general matrix notation, Mrxc shows that the matrix is named M and r is the number of rows and c is the number of columns. When multiplying two matrices, the number of columns in the first matrix must match the number of rows in the second matrix. In addition, when adding or subtracting matrices, the matrices must be of the same size.
The document Practice Questions: Matrices | Mathematics for ACT is a part of the ACT Course Mathematics for ACT.
All you need of ACT at this link: ACT
|
144 videos|100 docs|61 tests
|
FAQs on Practice Questions: Matrices - Mathematics for ACT
| 1. What are matrices in mathematics? |  |
Ans. Matrices are rectangular arrays of numbers, symbols, or expressions arranged in rows and columns. They are commonly used to represent and solve systems of linear equations.
| 2. How do you add and subtract matrices? | |
Ans. To add or subtract matrices, you simply add or subtract the corresponding elements in the matrices. The matrices must have the same dimensions for this operation to be valid.
| 3. What is the identity matrix? | |
Ans. The identity matrix is a square matrix where all elements are zero except for the diagonal elements, which are all one. It acts as the equivalent of the number 1 in matrix multiplication.
| 4. Can matrices be multiplied together? | |
Ans. Yes, matrices can be multiplied together, but the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix will have the number of rows of the first matrix and the number of columns of the second matrix.
| 5. How do you find the determinant of a matrix? | |
Ans. The determinant of a matrix is a scalar value that can be calculated using a specific formula based on the elements of the matrix. For a 2x2 matrix, the determinant is calculated by multiplying the top left element by the bottom right element and subtracting the product of the top right and bottom left elements.
Related Exams
About this Document
|
Dec 28, 2024 Last updated |
Document Description: Practice Questions: Matrices for ACT 2024 is part of Mathematics for ACT preparation.
The notes and questions for Practice Questions: Matrices have been prepared according to the ACT exam syllabus. Information about Practice Questions: Matrices covers topics
like and Practice Questions: Matrices Example, for ACT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Practice Questions: Matrices.
Introduction of Practice Questions: Matrices in English is available as part of our Mathematics for ACT
for ACT & Practice Questions: Matrices in Hindi for Mathematics for ACT course.
Download more important topics related with notes, lectures and mock test series for ACT
Exam by signing up for free. ACT: Practice Questions: Matrices | Mathematics for ACT
Description
Full syllabus notes, lecture & questions for Practice Questions: Matrices | Mathematics for ACT - ACT | Plus excerises question with solution to help you revise complete syllabus for Mathematics for ACT | Best notes, free PDF download
Information about Practice Questions: Matrices
In this doc you can find the meaning of Practice Questions: Matrices defined & explained in the simplest way possible. Besides explaining types of
Practice Questions: Matrices theory, EduRev gives you an ample number of questions to practice Practice Questions: Matrices tests, examples and also practice ACT
tests
|
Explore Courses for ACT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Summary
,Objective type Questions
,Sample Paper
,Viva Questions
,Practice Questions: Matrices | Mathematics for ACT
,video lectures
,mock tests for examination
,Previous Year Questions with Solutions
,Practice Questions: Matrices | Mathematics for ACT
,ppt
,study material
,Important questions
,practice quizzes
,MCQs
,Free
,past year papers
,Exam
,Extra Questions
,Practice Questions: Matrices | Mathematics for ACT
,shortcuts and tricks
,Semester Notes
;
Additional Information about Practice Questions: Matrices for ACT Preparation
Practice Questions: Matrices Free PDF Download
The Practice Questions: Matrices is an invaluable resource that delves deep into the core of the ACT exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Practice Questions: Matrices now and kickstart your journey towards success in the ACT exam.
Importance of Practice Questions: Matrices
The importance of Practice Questions: Matrices cannot be overstated, especially for ACT aspirants.
This document holds the key to success in the ACT exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Practice Questions: Matrices Notes
Practice Questions: Matrices Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Practice Questions: Matrices.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Practice Questions: Matrices Notes on EduRev are your ultimate resource for success.
Practice Questions: Matrices ACT
The "Practice Questions: Matrices ACT Questions" guide is a valuable resource for all aspiring students preparing for the
ACT exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Practice Questions: Matrices on the App
Students of ACT can study Practice Questions: Matrices alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Practice Questions: Matrices,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Practice Questions: Matrices is prepared as per the latest ACT syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup